图的存储结构 | 十字链表与邻接多重表存储结构
作者:互联网

十字链表存储结构
十字链表(Orthogonal List)是有向图的另一种链式存储结构,可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表,在十字链表中,有向图中每一条弧对应十字链表中的弧结点,而每一个顶点对应十字链表中的表头结点,如下所示:
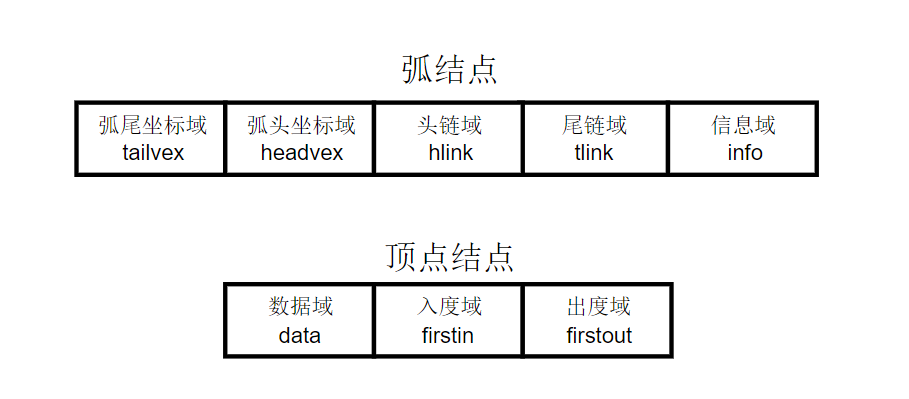
在弧结点中有五个域,其解释分别如下:
- 弧尾坐标域(tailvex):指示弧尾顶点在图中的位置
- 弧头坐标域(headvex):指示弧头顶点在图中的位置
- 头链域(hlink):指向弧头相同的下一条弧(即入度边)
- 尾链域(tlink):指向弧尾相同的下一条弧(即出度边)
- 信息域(info):该弧的相关信息
弧头相同的弧在同一链表上,弧尾相同的弧也在同一链表上,它们的头结点即为顶点结点,它由3个域组成:
- 数据域(data):存储和顶点相关的信息,如顶点名称等
- 头链(入度)域(firstin):指向以该顶点为弧头的第一个弧结点
- 尾链(出度)域(firsout):指向以该顶点为弧尾的第一个弧结点
如下图所示:
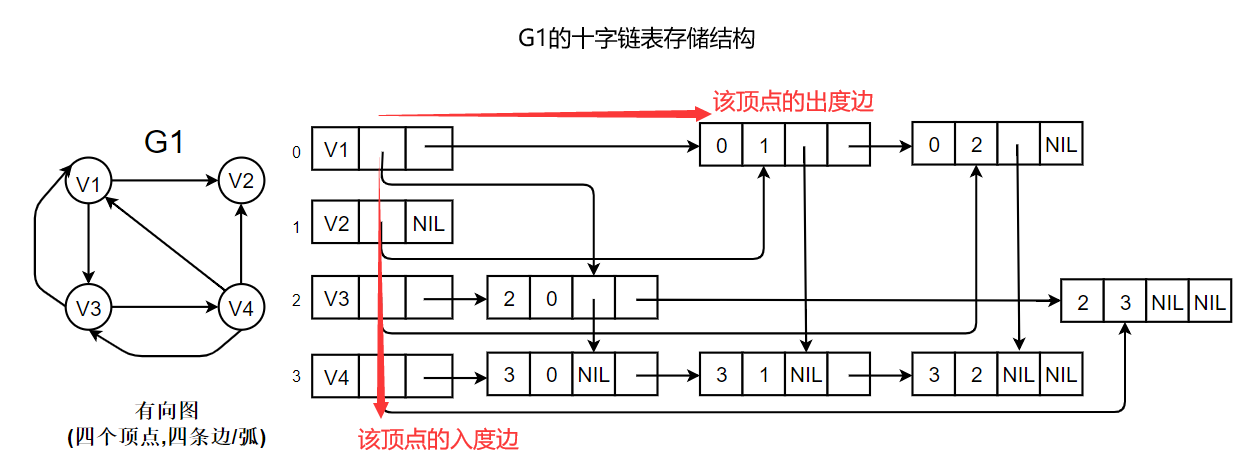
若将有向图的邻接矩阵看成是稀疏矩阵的话,则十字链表也可以看成邻接矩阵的链表存储结构,在图的十字链表中,弧结点所在的链表非循环链表,结点之间相对位置自然形成,不一定按顶点序号有序,表头结点即顶点结点,它们之间不是链接,而是顺序存储
简单来说,十字链表即是在顶点表中新增了一个链域,将逆邻接表与邻接表结合起来罢了
该存储结构的抽象数据类型定义如下所示:
//---------有向图的十字链表存储表示--------------
#define MAX_VERTEX_NUM 20
typedef struct ArcBox {
int tailvex, headvex;//该弧的尾和头顶点的位置
struct ArcBox* hlink, * tlink;//分别为弧头相同和弧尾相同的弧的链域
InfoType* info;//该弧相关信息的指针
}ArcBox;
typedef struct VexNode {
VertexType data;
ArcBox* firstin, * firstout;//分别指向该顶点第一条入弧和出弧
}VexNode;
typedef struct {
VexNode xlist[MAX_VERTEX_NUM];//表头向量
int vexnum, arcnum;//有向图的当前顶点数和弧数
}OLGraph;
只要输入 n 个顶点信息和 e 条弧的信息,便可建立该有向图的十字链表,其算法如下所示:
int LocateVex(OLGraph G,char e) {
for (int i = 0; i < G.vexnum; i++)
if (G.xlist[i].data == e) return i;
return -1;
}
Status Print_OLGraph(OLGraph G) {
for (int i = 0; i < G.vexnum; i++) {
printf("%d:", G.xlist[i].data);
ArcBox* p = G.xlist[i].firstin;
//p=G.xlist[i].firstout 逆邻接表
while (p) {
printf("[%d,%d]->", p->tailvex, p->headvex);
p = p->hlink;//邻接表
//p=p->tlink //逆邻接表
}
printf("\n");
}
return OK;
}
Status CreateDG(OLGraph* G) {
char tem;
scanf("%d,%d%c", &G->vexnum, &G->arcnum, &tem);
for (int k = 0; k < G->vexnum; k++) {
scanf("%c%c", &G->xlist[k].data,&tem);
G->xlist[k].firstin = G->xlist[k].firstout = NULL;
}
char v1, v2;
int In, Out;
ArcBox* p1;
for (int i = 0; i < G->arcnum; i++) {
printf("Input arc:");
scanf("%c,%c%c", &v1, &v2, &tem);
Out = LocateVex(*G, v1);//该弧的出度结点坐标
In = LocateVex(*G, v2);//该弧的入度结点坐标
if (In == Out == -1) return ERROR;
p1 = (ArcBox*)malloc(sizeof(ArcBox));
p1->headvex = In;//弧头顶点坐标
p1->tailvex = Out;//弧尾顶点坐标
p1->tlink = G->xlist[Out].firstout;
G->xlist[Out].firstout = p1;
p1->hlink = G->xlist[In].firstin;
G->xlist[In].firstin = p1;
p1->info = NULL;
}
Print_OLGraph(*G);
return OK;
}
如果在未来的某个场景中,需要频繁的计算出度和入度,需要知道一个顶点是不是另一个顶点的邻接点,还需要知道另一个顶点是不是该顶点的逆链接点,就可以使用十字链表。
数据结构就是用于开阔思维
邻接多重表存储结构
回顾一下在无向图的邻接表中,容易求得顶点和边的信息是优点,但是缺点也很明显,若需要在边上做操作(如删除)就需要修改两个顶点的链表
邻接多重表(Adjacency Multilist)是无向图的另一种链式存储结构,虽然邻接表是无向图的一种很有效的存储结构,它的结构和十字链表类似,在邻接多重表中,每一条边用一个结点表示,它由如下所示的6个域组成:
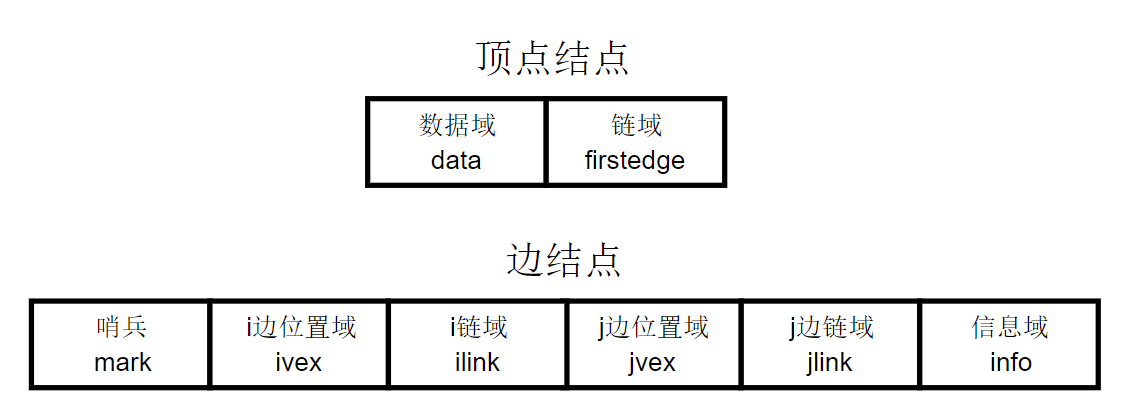
- 哨兵(mark):可用以标记该边是否被搜索过
- i边位置域(ivex):存储一条边两端其中一个顶点的坐标位置
- i链域(ilink):指向下一条依附于顶点ivex的边
- j链域(jvex):存储一条边两端其中一个顶点的坐标位置
- j链域(jlink):指向下一条依附于顶点jvex的边
而顶点结点有两个域,其中:
- 数据域(data):存储和该顶点相关的信息
- 链域(firstedge):指示第一条依附于该顶点的边
例如:
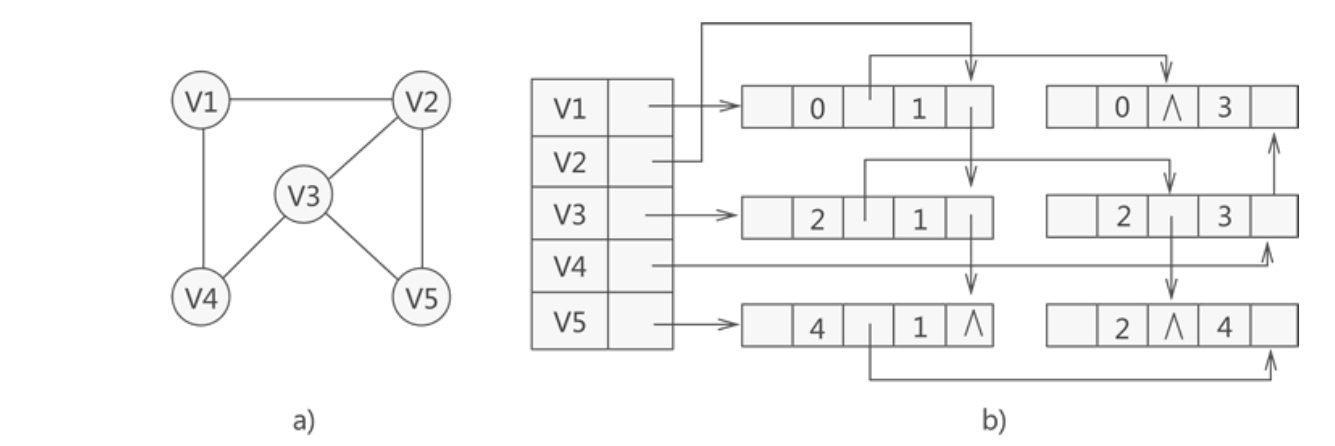
在邻接多重表中,所有依附于同一顶点的边串联在同一链表中,由于每条边依附于两个顶点,则每个边结点同时链接在两个链表中,可见,对无向图而言,其邻接多重表和邻接表的差别,仅仅在于同一条边在邻接表中用两个结点表示。
而在邻接多重表中只有一个结点,因此,除了在边结点中增加一个标志域外,邻接多重表所需的存储量和邻接表相同,在邻接多重表上,各种基本操作的实现亦和邻接表相似,邻接多重表的类型说明如下所示:
#define MAX_VERTEX_NUM 20
typedef enum { unvisited, visited }VisitIF;
typedef struct EBox {
VisitIF mark;//访问标记
int ivex, jvex;//该边依附的两个顶点的位置
struct EBox* ilink, *jlink;//分别指向依附这两个顶点的下一条边
InfoType* info;//该边信息指针
}EBox;
typedef struct VexBox {
VertexType data;
EBox* firstedge;//指向第一条依附该顶点的边
}VexBox;
typedef struct {
VexBox adjmulist[MAX_VERTEX_NUM];
int vexnum, edgenum;//无向图的顶点数和边数
}AMLGraph;
根据G2创建邻接多重表的算法如下所示:
int LocateVex(AMLGraph G,char e) {
for (int i = 0; i < G.vexnum; i++)
if (G.adjmulist[i].data == e) return i;
return -1;
}
Status Print_AMLGraph(AMLGraph G) {
printf("\n");
for (int i = 0; i < G.vexnum; i++) {
printf("V(%d):", G.adjmulist[i].data);
EBox* p = G.adjmulist[i].firstedge;
while (p) {
printf("(%d,%d)-->", p->ivex, p->jvex);
if (p->ivex == i)
p = p->ilink;
else
p = p->jlink;
}
printf("\n");
}
return OK;
}
Status CreateUDN(AMLGraph* G) {
char tem;
scanf("%d,%d%c", &G->vexnum, &G->edgenum, &tem);
for (int i = 0; i < G->vexnum; i++) {
scanf("%d%c", &G->adjmulist[i].data, &tem);
G->adjmulist[i].firstedge = NULL;
}
EBox* p1, * p2;
int v1, v2, i ,j ,weight;
for (int k = 0; k < G->edgenum; k++) {
scanf("%d,%d,%d%c", &v1, &v2, &weight, &tem);
i = LocateVex(G, v1);
j = LocateVex(G, v2);
if (i == -1 || j == -1 || i == j)
return ERROR;
//创建结点
p1 = (EBox*)malloc(sizeof(EBox));
p1->ilink = p1->jlink = NULL;
p1->ivex = i;
p1->jvex = j;
p1->weight = weight;
if (G->adjmulist[i].firstedge == NULL) {//若i顶点邻接表为空,则直接插入
p1->ilink = G->adjmulist[i].firstedge;
G->adjmulist[i].firstedge = p1;
}
else {//否则判断其第一个邻接点是与i相同还是与j相同,以此定位插入是在ilink域还是jlink域
p2 = G->adjmulist[i].firstedge;
if (p2->ivex == i) {//如果与i相同,则插进ilink域
p1->ilink = p2->ilink;
p2->ilink = p1;
}
else {//否则将其插入jlink域,这儿需要注意:
//因为新创建的结点i和j是恒定的位置,所以若新插入的结点的i与第一个邻接顶点的j相同
//则需要将其头插进第一个邻接顶点的jlink域
p1->ilink = p2->jlink;
p2->jlink = p1;
}
}
if (G->adjmulist[j].firstedge == NULL) {
p1->jlink = G->adjmulist[j].firstedge;
G->adjmulist[j].firstedge = p1;
}
else {
p2 = G->adjmulist[j].firstedge;
if (p2->jvex == j) {
p1->jlink = p2->jlink;
p2->jlink = p1;
}
else {
p1->jlink = p2->ilink;
p2->ilink = p1;
}
}
}
return OK;
}
标签:存储,p1,int,结点,链表,邻接,顶点,结构 来源: https://www.cnblogs.com/RioTian/p/16437584.html