最近公共祖先(LCA)(RMQ)

最近公共祖先(LCA)(RMQ)

作为求LCA的常见方法之一，RMQ算法可以以O(nlogn)的复杂度初始化，然后以O(1)的复杂度进行查询。RMQ(Range Minimum/Maximum Query)意为区间最值查询，即查找区间[l,r]中元素的最大/小值。但今天讨论的算法是有关树的，因此我们要想办法把树转换成一个满足我们需求的序列。

欧拉序

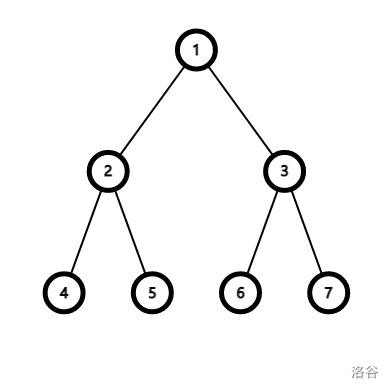
如图，这棵树的其中一个欧拉序为1,2,4,2,5,2,1,3,6,3,7,3,1。它其实是对树从根节点开始进行一个dfs，每个节点在进入子树之前记录一次、退出之后记录一次。这样的好处是任意两个节点的最近公共祖先一定是在他们之间，且是他们之间元素中层数最小的那一个。因此，对于每对询问的节点A和B，我们只要找到A和B在欧拉序中第一次出现的位置a和b，则他们的最近公共祖先一定是区间[a,b]中层数最小的元素。
但我们应当如何找到区间[a,b]中层数最小的元素呢？用st表解决。

代码

#include<bits/stdc++.h>
using namespace std;
int n,m,s,x,y,a,b;
vector<int> tmap[10000010];
int dep[10000010];
int dfso[10000010],down=1;
int st[10000010][30];
int numo[10000010]={0};
void dfs(int st,int fa,int d)//dfs一遍,求出层数、欧拉序
{
	if(numo[st]==0)numo[st]=down;
	dep[st]=d;
	dfso[down++]=st;
	for(auto i:tmap[st])
	{
		if(i==fa)continue;
		dfs(i,st,d+1);
		dfso[down++]=st;
	}
}
void st_init()//初始化st表
{
	for(int i=down-1;i>=1;i--)
	{
		st[i][0]=dfso[i];
		for(int j=1;j<20;j++)
		{
			if(i+(1<<(j-1))>(down-1))break;
			st[i][j]=dep[st[i][j-1]]<dep[st[i+(1<<(j-1))][j-1]]?st[i][j-1]:st[i+(1<<(j-1))][j-1];
		}
	}
}
int fnd(int a,int b)//O(1)查找
{
	int l=numo[a],r=numo[b];
	if(l>r)swap(l,r);
	int k=log2(r-l+1);
	return dep[st[l][k]]<dep[st[r-(1<<k)+1][k]]?st[l][k]:st[r-(1<<k)+1][k];
}
int main()
{
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<n;i++)
	{
		scanf("%d%d",&x,&y);
		tmap[x].push_back(y);
		tmap[y].push_back(x);
	}
	dfs(s,s,1);
	st_init();
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&a,&b);
		printf("%d\n",fnd(a,b));
	}
	return 0;
}

标签：10000010,RMQ,祖先,dfso,st,down,int,LCA
来源： https://www.cnblogs.com/huled/p/16434205.html