[AGC036F] Square Constraints

一、题目

点此看题

二、解法

根据 \(\tt EI\) 所说：尝试利用各种意义上的直观。我们把问题放在二维平面上，那么问题变成了，在两个圆之间的圆环区域中放置 \(2n\) 个车，要求车都放在整点上，且互不攻击的方案数，如图：

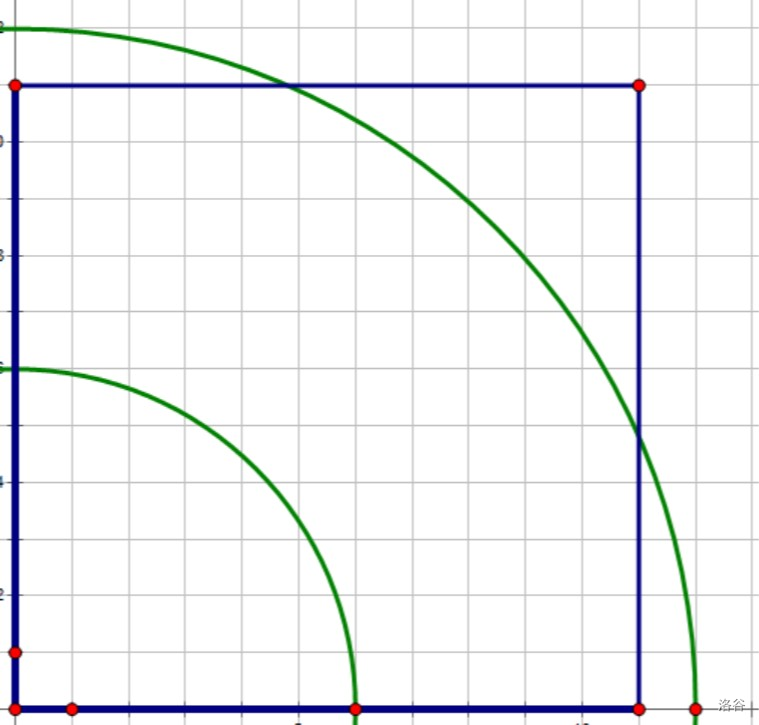
设每个点可放置的上下边界分别是 \([L_i,R_i]\)，但这样貌似还是不好做。考虑简化问题，先思考只有上边界的情况怎么做。发现从右往左可以选择的范围越来越大，设 \(R\) 排序后的结果是 \(R'\)，那么方案数是：

\[\prod_{i=0}^{2n-1} R'_i-i+1 \]

再把下边界加上去，首先我们把整个图分成 \([0,n)/[n,2n)\) 两部分，然后容斥 \(i\in[0,n)\) 中点在 \([0,L_i)\) 中的个数。

很可惜的是，我们并不能知道所有 \([0,L_i)\) 和 \([0,R_i]\) 混合排序的结果，但是可以知道一个大致的排序结果。具体来说我们把 \([0,n)\) 中的点键值设为 \(L_i-1\)，把 \([n,2n)\) 中点的键值设置为 \(R_i\)，然后排序。

设 \(dp[i][j]\) 表示考虑了排序之后的前 \(i\) 个位置，已经选取了 \(j\) 个 \(L\) 的方案数，转移分三种大情况讨论：

① 如果当前遇到的位置原来在 \([n,2n)\) 中：

• 初始有 \(R_i+1\) 个方案。
• 前面选择过 \(L\) 的，在最终排序序列中都会在他前面，减少 \(j\) 个方案。
• 前面原来位置在 \([n,2n)\) 中的，设有 \(c_1\) 个，会减少 \(c_1\) 个方案。
• 所以总方案数是 \(R_i+1-j-c_1\)

② 如果当前遇到的位置原来在 \([0,n)\) 中，并且选 \(L\)：

• 初始有 \(L_i\) 个方案。
• 与第一种情况类似，减少 \(c_1+j\) 个方案。
• 所以总方案数是 \(L_i-j-c_1\)

③ 如果当前遇到的位置原来在 \([0,n)\) 中，并且选 \(R\)，这种情况略微有点复杂：

• 初始有 \(R_i+1\) 个方案。
• 所有将要选择 \(L\) 的都要排在它前面，设总数是 \(k\)，那么减少 \(k\) 个方案。
• 所有 \([n,2n)\) 都会排在它前面，那么减少 \(n\) 个方案。
• 前面选择过 \(R\) 的也会排在它前面，设前面原来位置在 \([n,2n)\) 中的有 \(c_2\) 个，那么减少 \(c_2-j\) 个方案。
• 所以总方案数是 \(R_i+1-n-k-c_2+j\)

发现上述转移中我们唯一不能确定的就是 \(k\)，所以我们在外层枚举 \(k\)，最后得到的方案数就是 \(dp[2n][k]\)，我们再对这个方案数进行容斥即可，时间复杂度 \(O(n^3)\)

三、总结

尝试借助各种工具，或者各种类型的直观。其一是用图上几何直观，借助几何图形在大脑中的呈现来考虑问题。其二是符号演算，利用基于符号所重塑的新直观来进一步考虑问题。

如果计数顺序不明确时，可以确定一个大致的顺序，然后在计数的过程中修正它。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int M = 255;
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,ans,dp[M<<1][M];pii p[M<<1];
void add(int &x,int y) {x=(x+y)%m;}
int calc(int k)
{
	memset(dp,0,sizeof dp);
	dp[0][0]=1;int c1=0,c2=0;
	for(int i=1;i<=2*n;i++)
	{
		if(p[i].se==0)//[n,2n)
		{
			for(int j=0;j<=c2;j++)
				add(dp[i][j],dp[i-1][j]*(p[i].fi-c1-j+1));
			c1++;
		}
		else//[0,n)
		{
			for(int j=0;j<=c2;j++)
			{
				add(dp[i][j+1],dp[i-1][j]*(p[i].fi-c1-j+1));
				add(dp[i][j],dp[i-1][j]*(p[i].se-k-n-c2+j+1));
			}
			c2++;
		}
	}
	return dp[2*n][k];
}
signed main()
{
	n=read();m=read();
	for(int i=0;i<n;i++)
	{
		p[i+1].fi=ceil(sqrt(n*n-i*i))-1;
		p[i+1].se=floor(sqrt(4*n*n-i*i));
		p[i+1].se=min(p[i+1].se,2*n-1);
	}
	for(int i=n;i<2*n;i++)
	{
		p[i+1].fi=floor(sqrt(4*n*n-i*i));
		p[i+1].fi=min(p[i+1].fi,2*n-1);
	}
	sort(p+1,p+1+2*n);
	for(int i=0;i<=n;i++)
	{
		if(i&1) ans=(ans+m-calc(i))%m;
		else ans=(ans+calc(i))%m;
	}
	printf("%lld\n",(ans+m)%m);
}

标签：方案,Square,前面,AGC036F,排序,2n,include,数是,Constraints
来源： https://www.cnblogs.com/C202044zxy/p/16411931.html