LeetCode 2090. K Radius Subarray Averages

原题链接在这里：https://leetcode.com/problems/k-radius-subarray-averages/

题目：

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

• For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.

Example 1:

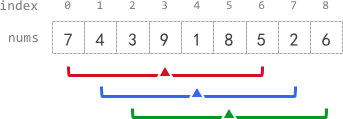
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.

Example 2:

Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input: nums = [8], k = 100000
Output: [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0. 

Constraints:

• n == nums.length
• 1 <= n <= 105
• 0 <= nums[i], k <= 105

题解：

Have a window to maintain the sum. Window size is 2 * k + 1, save it as len.

if nums.length < len. Then we could simply return array containing only -1.

Move runner, update sum. When runner - walker = len, we need to update the result.

res[walker + k] = average.

Then move walker by 1 and substract the corresponding value from sum.

Note: there could be overflow. The sum type is long.

Time Complexity: O(n). n = nums.length.

Space: O(1). regardless res.

AC Java:

 1 class Solution {
 2     public int[] getAverages(int[] nums, int k) {
 3         if(nums == null || nums.length == 0 || k == 0){
 4             return nums;
 5         }
 6         
 7         long sum = 0;
 8         int [] res = new int[nums.length];
 9         Arrays.fill(res, -1);
10         int len = 2 * k + 1;
11         if(nums.length < len){
12             return res;
13         }
14         
15         int walker = 0;
16         int runner = 0;
17         while(runner < nums.length){
18             sum += nums[runner++];
19             if(runner - walker == len){
20                 res[walker + k] = (int)(sum / len);
21                 sum -= nums[walker++];
22             }
23         }
24         
25         return res;
26     }
27 }

类似Minimum Size Subarray Sum.

标签：index,nums,int,sum,length,Radius,Subarray,avg,Averages
来源： https://www.cnblogs.com/Dylan-Java-NYC/p/16378016.html