面向对象第三单元总结
作者:互联网
面向对象第三单元总结
fishlife
目录写在前面
程序员都是不可信任的 ——荣文戈
上单元末提到的至理名言在这个单元应验了。
老实说,这个单元的编程难度确实不难,难点在于阅读和理解规格。因为对于部分方法,规格本身就占据了相当大的篇幅,想要通读并理解自然需要些时间和精力。再加上隐藏在大篇幅规格内的一些不起眼的规则极易被忽视,这就容易导致最后呈现的代码并不符合规格要求,并且用JUnit都很难测出来(原因之后会讲)。
所以,JML从来都不是一个简单的单元。
本单元关键词:图论复习与阅读理解
图论复习指的是这个单元本身就以一个社交网络的建立作为引导来让我们学习JML风格。并且从第一次作业到第三次作业,我被作业推动着依次复习了可达性判定算法,最小生成树算法和最短路径算法。
阅读理解这个词无需多言。阅读规格这件事确实就是在做阅读理解,必须得仔细地看过每一行,不放过任何一个写明的规格之外,还需要去理解这些规格对应到程序语言时要表达的意思以及规格之间的联系。
分次作业分析
分次作业分析将对每次作业从架构设计(主要是图模型部分),算法及性能分析及优化,测试,bug情况四部分展开。
为方便叙述,这里将我实现官方接口时用的一个命名标准如下,后续出现类似名字时不再解释。
- 类Social[name]对应实现官方接口[name]。
由于本单元第一次作业(即第九次作业)具有奠基性作用,所以这次作业我会写得比较详细,主要是对一些通用架构和通用测试方法的描述,后续作业中不会对这些部分再次叙述。而其他作业则会从迭代的角度进行阐述,可能篇幅会短于第九次作业。
第九次作业
每一单元作业的第一次作业都具有奠基的作用。所以这一部分我完成的时间比较长,以防止后期反反复复的重构。
总架构上,由规格,NetWork级别必定存在两个容器,分别用于存放Person和Group信息。通读所有的JML规格可知,Person之间与Group之间以ID作为唯一标识,且不对其加入网络的顺序有任何查询请求,因此在SocialNetwork里选择采用HashMap对上述信息进行存储。键为ID,值为对应的Person或Group。同理,在SocialGroup里,也采用HashMap来存储组内的Person信息。这样可以快速地检索到对应的Person或Group。
图模型构建与维护
本单元中,Group实际上不涉及与图相关的内容,所以只需考虑Person和Network即可。
由JML规格,Person就是整个社交网络图中的节点,而Network则是整个社交网络图。可以发现官方并没有给我们提供与“边”相关的接口。为方便起见,这里我自定义了一个“边”类Relation。
public class Relation {
private int value;
private Person person;
public Relation(int value, Person person) {
this.value = value;
this.person = person;
}
public int getValue() {
return value;
}
public Person getPerson() {
return person;
}
}
其中,value表示边权,而Person表示该边指向的Person。对应地,每个Person就会有一个储存Relation的容器。虽然Relation作为自定义类并没有ID标识,但是其指向的Person是有唯一ID标识的。并且通读JML可知,不可能出现重边(出现重边会报异常),且同样不对边加入网络的顺序有任何查询请求。所以我选择在Person内使用HashMap来存储Relation,键为指向的Person的ID,值为对应的Relation。这样我们便能构造出下图所示的基本单元。
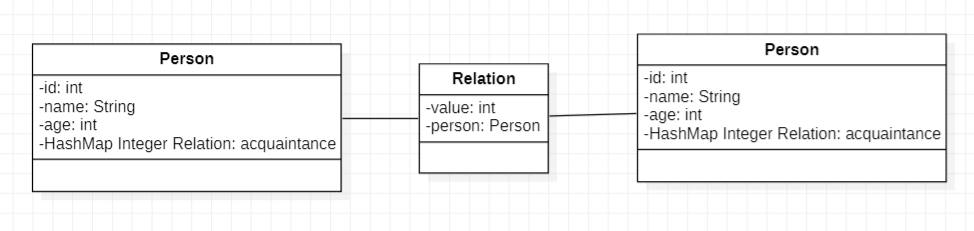
整个网络便会以此为基本形式展开。
由JML可知,整个Network为无向图。而上述对Relation的定义是有方向的。所以执行ar指令时,需要将边的信息分别加入在边的始末位置对应的Person对象内,以维护无向图。
算法及性能分析
本次作业涉及到图论算法的方法是isCircle和queryBlockSum。前者用于判断两个人是否有直接或间接的联系,后者用于判断该社交网络中拥有的连通分支的数量。但二者涉及的其实是同一类算法:可达性判定算法。
先讨论第一个方法。判断两个人是否有直接或间接的联系其实就是判断两个节点之间有没有通路。一个最容易想到的算法就是DFS,从初始点开始,如果连接到的点为终点则返回true,否则对所有与其有边的点做DFS。想法很简单,但是很明显,这种做法的时间复杂度为\(O(N+E)\),其中N为顶点数,E为边数,且由于递归操作还涉及到压栈的问题,真正耗费的时间会比这个要长一点。所以直接DFS的做法是很可能超时的(经同学检验,确实会超时)。所以保险起见,我们需要一些其他的手段。
网上冲浪以及助教的帖子可知,可达性判定有个非常好用的算法叫做并查集。具体思想其实就是将在一个连通分支里的点归到一个集合里,看成一个等价类。然后判断二节点可达时只需要判断两个节点是否在同一集合里即可。时间复杂度为\(O(1)\)到\(O(n)\)。
要使用并查集,就得需要做好对并查集的维护。一般并查集实现是采用树的形式,将与某个节点连接的节点作为该节点的子节点加入到并查集森林中,判断两节点是否可达时只需要对两节点不断向上寻找其父节点,如果其具有相同的父节点则表示他们可达(有直接或间接联系),否则不可达。但如果整个树退化成一条链的话,这种做法的复杂度便会退化为\(O(n)\),不利于提高效率。而因为此时并不需要我们知道具体的路径,只需要知道两个节点是否有相同父节点即可。所以可以采用路径压缩进行优化。将所有具有相同父节点的节点全部连接到最上层的那个父节点的下面,使这些点全部成为最上层父节点的直接子节点。路径压缩效果如下图所示。
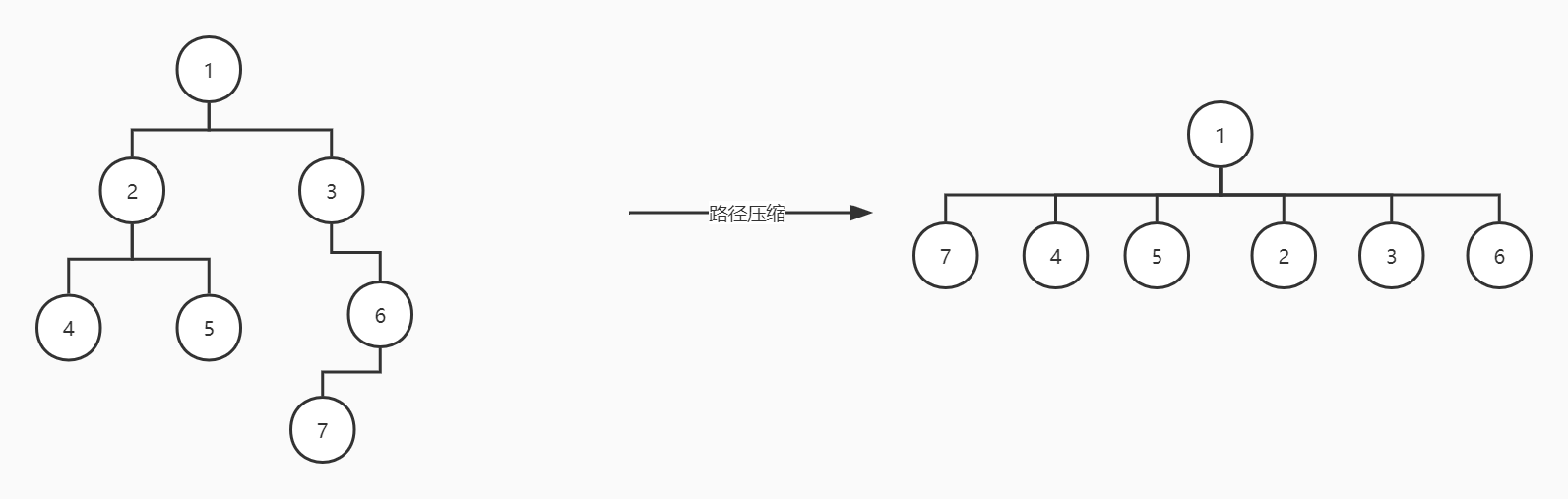
这样我们便可把时间复杂度压缩到\(O(1)\)。代码上其实也不需要做过多处理,只需要在原来递归查找父节点时,顺带着将查找过的节点的父节点更新即可。
为了支持并查集,需要在SocialNetwork内添加存储并查集森林的容器。由于节点和节点的关系就是Person和Person间的关系,Person有唯一ID标识,且不会出现重边的情况。所以可以用一个HashMap来表示节点和其父节点的关系,键为PersonId,值为其父节点的PersonId。为了方便之后对连通分支数量的查询,所以加入一个HashSet用于存储当下所有并查集树的根节点ID。最后写出来的用于实现isCircle主要逻辑的函数如下。
private int find(int id) {
if (parent.get(id) == -1) {
return id;
}
int newparent = find(parent.get(id));
parent.put(id, newparent);
return newparent;
}
其中当一个节点的父节点ID为-1时表示其为根节点。并且在寻找根节点时顺便将沿途所有遍历到的节点均进行了更新。最后,只需要判断两个点所在并查集树的根节点ID是否相等即可。
而既然已经实现了并查集,那么queryBlockSum的实现就比较简单了,直接返回存储了根节点的集合大小即可。但此时需要我们去维护整个并查集。即当遇到下图左边的情况时,即两个并查集根节点之间新加一条边时,需要做合并操作将其合并到一棵树上,同时将被合并的树的根节点ID从集合中删去,变成下图右边的情况,才能继续使用并查集算法。
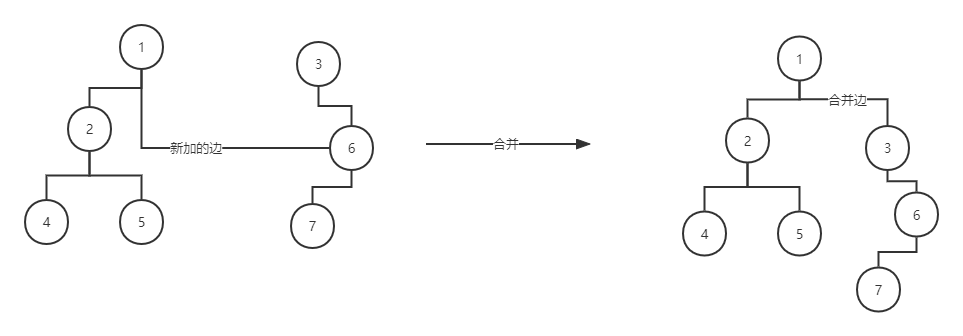
合并的函数如下所示。
private void merge(int id1, int id2) {
int parent1 = find(id1);
int parent2 = find(id2);
if (parent1 != parent2) {
parent.put(parent1, parent2);
root.remove(parent1);
}
}
而此时我们不需要去管理被合并的两个根节点下面的那些节点是否在并查集树上直接连接到了根节点上,因为在之后对这些节点的执行find函数时会自动更新这些节点对应的根节点值,维护并查集和路径压缩。
综上,我们用并查集算法实现了isCircle和queryBlockSum。算法复杂度为\(O(1)\)。显然不会超时,性能过关。
测试
测试方面总体采取的策略是正确性测试+随机大量数据测试+极端数据测试三部分组成。其中第一部分和第三部分与JML规格关联度比较大。
正确性测试其实就是编写好数据后对照JML规格,通过JUnit的各种assert方法来判断程序运行过程中是否出现问题。其中和我们平常做的黑盒测试明显不同的地方在于,我们不能只通过结果的正确性来判断程序的正确性。JML规格实际上对我们的程序做了更加严格的约束。一个例子就是JML规格中的不变式,这要求我们程序在可见状态下不变式必须要被满足,亦即JML对程序执行的过程也进行了严格的限制。这也导出了依靠JML和JUnit组合进行测试时使用的一个经典方法:在类里面撰写一个repOK方法用于判定此时类是否符合不变式,在每个方法执行前后各执行一次repOK即可实现对不变式的判定。在JUnit中,只需将repOK方法置于@Before和@After内即可。
@Before
public void before() throws Exception {
repOK();
//do other thing
}
@After
public void after() throws Exception {
repOK();
//do other thing
}
随机大量数据测试的目的是测试程序的鲁棒性,测试那些可能不是由于方法实现的正确性和合规性而导致的错误。这里因为输入数据的格式固定且有规律可循,并且对于不同的实现,正确的输出是一样的,所以这里采用了数据生成器和对拍器组合的评测机的策略。数据采用纯随机生成的方式,并且通过随机数来控制“异常报出的比例”,从而兼顾到程序的正常处理功能和异常处理功能这两个最主要功能的测试,其中出错的部分会通过输出的文本文件知悉具体错误位置和原因(该评测机能测试WA和TLE两种错误)。
line 4993 error!
Your output: einf-94, 28-3
Other output: einf-97, 28-3
Two outputs have different line numbers!
output lines isn't equal to command num!
command num: 5001
output num: 5000
Error code: 11000727
极端数据测试则是进一步测试程序的鲁棒性。一般是根据JML规格和指导书限制手动构造极端数据来测试程序是否会超时。在本次作业中,最可能超时的就是上面我们花了大篇幅介绍算法的isCircle和queryBlockSum。因此可根据规格构造如下的数据。
ap 1 1 200
ap 2 2 200
...
ar 1 2
ar 2 3
ar 1 3
...
qbs
qbs
...
qci 1 2
...
即只用ap和ar构造一张尽量复杂的图,然后不断调用qbs或者qci,尝试着让程序超时。但是这次作业给的指令数量比较小,并且并查集本身的时间复杂度也很低,所以这种做法在课下自己测试时较难起到hack超时的作用,更多是变成了测试qci指令正确性的一种手段。
bug情况
本次作业未被测出bug。
第十次作业
这次作业主要新增了收发消息的机制。并且网络内的消息和个人拥有的消息是独立的。因此需要在SocialNetwork和SocialPerson里各增加一个容器来存放消息。由于message也具有唯一ID标识,所以在SocialNetwork里也可以使用HashMap来存储message。键为ID,值为Message。但是在Person中,通读JML可知,需要提取“最近4条接收到的消息”,亦即对Message的加入顺序有要求。但是却不要求对Message通过ID随机检索的功能,所以这里使用LinkedList更合适。(原本我的代码实现中用的是ArrayList,在所有作业都已经截止后经同学提醒发现此处涉及到的操作全是头插操作,显然LinkedList的效率要远大于ArrayList,特此说明)。
图模型构建与维护
本次作业中图结构保持不变。
算法与性能分析
本次作业涉及到图论算法的方法是queryLeastConnection,涉及到的算法是最小生成树算法。最小生成树的两个经典算法是Prim算法和Kruskal算法。前者在稠密图下效果更好,后者在稀疏图下效果更好。由于Krukskal算法需要从一个全局的视角去选择要将哪条边加入已选边集合,而我已实现的图中并没有一个全局存放边的装置,不太容易实现Kruskal。加上笔者本人比较熟悉Prim算法,所以笔者选择Prim算法。
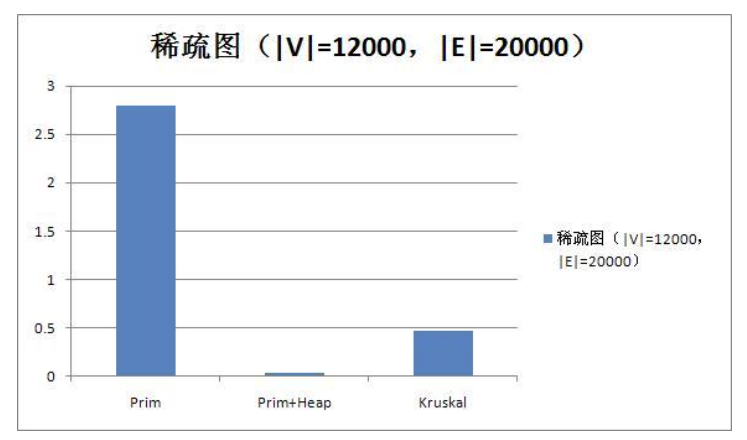
上图是对一张节点数12000,边数为20000的稀疏图上跑各种算法求最小生成树得出来的时间柱状图。虽然我们的输入达不到这个体量(输入限制10000条指令),但是我们还是能从中得到一些启发。从上图中可以看出,如果要使用Prim算法,基本上堆优化是不可避免的,因为上述图表是使用C++程序跑出来的结果,而Java比C++慢的不是一星半点。C++尚且需要接近3s的时间,Java的话10s显然是完全不够的。所以我们需要进行堆优化,将时间复杂度从\(O(n^2)\)压到\(O(nlogn)\)。而从上图也可以看出,使用堆优化能够极大地减小我们程序的运行时间。
Prim算法的具体实现细节讨论区和网上都有,这里就不再赘述。堆优化实际上就是缩短Prim算法中”找到离当前节点’最近‘(路径边权和最小)的节点”这一步的时间。我们只需要以路径边权和为标准维护一个小顶堆,每次选择节点时直接取堆顶的那个节点即可。而Java提供了PriorityQueue来实现类似小顶堆的功能。最终算法代码如下。
@Override
public int queryLeastConnection(int id) throws PersonIdNotFoundException {
if (!people.containsKey(id)) {
throw new SocialPersonIdNotFoundException(id);
}
HashSet<Integer> chosenSet = new HashSet<>();
int nextId = id;
int edgeSum = roots.get(find(id)).getNum() - 1;
ArrayList<Relation> chosenEdges = new ArrayList<>();
HashMap<Integer, Relation> edgeMap = new HashMap<>();
PriorityQueue<Relation> relations = new PriorityQueue<>(
Comparator.comparingInt(Relation::getValue)
);
for (int edgeNum = 0;edgeNum < edgeSum;edgeNum++) {
chosenSet.add(nextId); //加入新节点
for (Relation relation:
((SocialPerson) (people.get(nextId))).getAcquaintance().values()) { //遍历所有与其相连的边
int personId = relation.getPerson().getId();
if (!chosenSet.contains(personId) && (!edgeMap.containsKey(personId)
|| edgeMap.get(personId).getValue() > relation.getValue())) { //连接的点不能在已选集合内, 当前集合无到该节点的边或用更小权值的边替代
edgeMap.put(personId, relation);
relations.add(relation);
}
}
Relation chosenRelation;
while (true) { //选择那条最小权值的边
chosenRelation = relations.poll();
if (!chosenSet.contains(chosenRelation.getPerson().getId())) {
break;
}
}
chosenSet.add(chosenRelation.getPerson().getId());
chosenEdges.add(chosenRelation);
edgeMap.remove(chosenRelation.getPerson().getId());
nextId = chosenRelation.getPerson().getId();
}
int sumValue = 0;
for (Relation relation: chosenEdges) {
sumValue += relation.getValue();
}
return sumValue;
}
可以发现,这里笔者维护的小顶堆有一点不同,里面维护的其实是连向某个节点的“虚边”,该边权值等于当前节点与该虚边指向节点的实际路径边权和。实际上可以看到,这个堆里面是会存放连向同一节点的不同虚边的。因为在遍历下一个节点时上一个节点存入的虚边并未被剔除,而笔者并没有采用将该边的权值更新的方式,因为这需要遍历队列,很耗费时间。笔者采用的是若这条虚边的权值确实短于原来的那条虚边(可通过edgeMap快速查找到),则直接将这条虚边塞入堆中。由优先队列的性质,这条虚边所处的位置一定在原来那条虚边之前。在取堆元素的过程中一定会先取到更短的这条,符合我们的要求。而另外那条更长的边留在堆里其实没有关系,因为当取到这条边时会发现这条边所指向的节点已经加入到已选节点集合中,所以程序会抛弃这条边转而去取下一条边。
这样我们便用堆优化版的Prim算法实现了queryLeastConnection方法,时间复杂度为\(O(nlogn)\),不会超时。
测试
测试的方式还是和上次作业一样采用正确性测试+随机大量数据测试+极端数据测试三个层次递进的方式。
正确性测试依旧是采用JUnit对照规格进行测试,这里倒没有什么特别的,就是对照规格,编写测试类,然后测试就可以了。(埋下伏笔)这里正确性测试花比较大功夫的地方是消息传送机制的测试。因为这里涉及到“私聊”和“群发”两种传送方式,都需要保证“该收到消息的人收到了,不该收到消息的人不能有任何变化”这一点。不过这里我们采用了HashMap来精确检索接收方(群发时则是直接遍历组内所有的人),所以只要往社交网络以及往组内加人时不出差错,这一块出错的概率不是很大。
随即大量数据测试因为有第九次作业的评测机作为基础,所以本次作业的评测机搭起来相当地迅速。事实上,只需要在原评测机的数据生成器多加几个函数用于生成新的指令就可以了。
极端数据测试主要还是针对queryLeastConnection进行的,和之前的isCircle一样,这也是很容易被报超时的点,同时由于笔者采用了堆优化,也可能在优化过程中产生差错。所以这次测试是很有必要的。至于构造方法也很简单,因为笔者采用的Prim算法在稀疏图下时间复杂度是比较大的,所以用稀疏图的数据来测试是一个比较好的选择。并且稀疏图的数据相较于稠密图而言反倒更好制造,因为稠密图边多,为了充分利用给定的10000条指令,每次生成时都需要考虑到有没有可能因重边而导致“浪费"了这条指令的情况。稀疏图则是点比较多,就比较难出现重边的情况。具体的一个生成的样例如下所示。
ap 1 1 128
ap 2 2 15
ap 3 3 141
ap 4 4 177
ap 5 5 3
ap 6 6 48
ap 7 7 36
...
ar 1 909 915
ar 2 322 920
ar 2 549 198
ar 2 562 346
ar 3 270 723
ar 3 504 517
ar 3 587 224
ar 3 681 441
ar 3 839 692
ar 3 924 464
ar 4 85 991
ar 4 352 271
...
qlc 1
qlc 2
qlc 3
qlc 4
qlc 5
qlc 6
...
从样例中可以看出,本地测试的时候一般都是会采用超出指导书上限的更加高压的数据来进行测试,以确保我们的程序能够万无一失地通过强测和互测。而且我很幸运地卡出了我的程序的一个上限:1200个点,约50000条边,1200次qlc指令,这个点可以让我的程序运行时间稳定在10s左右,卡着CTLE的线过关。但我们的指令限制显然达不到这个水平,所以性能上这里没吃太多的亏。
bug情况
这次强测没出问题,互测则成为了我第一次,也是唯一一次被查出两个bug的一次互测。
一个bug就是1111的bug,说实话这一条规格我怀疑没有在最初始的JML作业里,应该是在某一代助教那里给加上去的,因为看起来合法但是没什么理由。具体而言,就是我忽视了下面的这条JML规格。
...
@ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id2) &&
@ (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1) &&
@ getGroup(id2).hasPerson(getPerson(id1)) == false &&
@ getGroup(id2).people.length < 1111;//忽略了这条
@ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id2) &&
@ (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1) &&
@ getGroup(id2).hasPerson(getPerson(id1)) == false &&
@ getGroup(id2).people.length >= 1111;//忽略了这条
这里就有个问题:明明都用JUnit测试过正确性了,为什么还会出现这种错误呢?这就要提到我在讨论课上提出过的一个观点。JUnit的一个美中不足之处就在于其测试函数依旧需要人去编写,而测试函数的正确性只能依赖于程序员对JML规格的理解。一旦理解是错的,那么编写的测试函数自然也是错的。测试的结果自然是不可信的。
就比如上面这个例子,实际上一句JUnit就可以解决
ap 1 1 200
...
ap 1112 1112 200
ag 1
atg 1 1
...
atg 1 1112
//上面是测试样例
//下面是JUnit语句
assertTrue(group.get(1).getSize <= 1111);
但很显然,如果忽视了上面这条规格的话,笔者不会去想到写这么一句assert,也就很难通过JUnit来查出这个bug。而且,这个数据某种意义上也算是一种极端数据,随机生成数据很难产生出一个满员的组,所以程序也顺利通过了随机大量数据测试。极端数据测试主要考虑的是超时问题,压根就没往这个方向想,自然也就查不出这个bug,最终导致在互测阶段”翻车“。
debug显然也是个很简单的活,只需要加组员时多一句条件判断即可。
if (group.getSize() < 1111) {
group.addPerson(person);
} //why 1111?
这里出错确实是由于笔者个人疏忽导致的,可能无法印证笔者的观点。但是之后会提到的一个bug则确实印证了上述关于JUnit的结论。
另一个bug则是一个性能bug,但是问题不出在上面那个复杂的图论算法上,而是出在SocialGroup的getValueSum方法上。因为在计算组内点之间连接的边权总和时,我采用了非常暴力的二重循环,显然时间复杂度\(O(n^2)\)。极易导致超时,所以容易被下面这样的样例hack。
ap 1 1 200
...
ap 1111 1111 200
ag 1
atg 1 1
...
atg 1 1111
qgvs 1
qgvs 1
...
qgvs 1
经试验,5000条指令的样例需要29s才能跑完,已经远远超出了时间限制。
debug的方法也比较简单,因为这个方法只需要计算连接组内两点的边,所以其实只需要将遍历的第二层改为遍历当前Person具有的边即可。有些人可能会觉得说那我造一个点让一个节点连接了一大堆组外的边(连接组内点的边本身就要计算,所以不是无效运算),这样不还是很容易超时。但事实上,由于异常机制的存在,边要成功建立必须得保证两个节点都已经存在于网络中,而如果要实现上面的那种数据点,指令的开销是非常大的(加人一条指令+加边一条指令,至少指令数翻倍)。因此要使该数据点达到\(O(n^2)\)的效果,所需的指令数量会远远大于现有指令数。所以在现有条件下不用担心超时问题,并且改进后的设计也更加符合逻辑。
第十一次作业
第十一次作业加入了更加复杂的消息传递机制。通读JML可知,新增的EmojiMessage必须要有一个容器对其进行管理。从JML了解到Emoji本身也有ID作为唯一标识,并且不要求对其加入顺序进行查询操作,所以SocialNetwork内依旧采用HashMap对其进行管理。为方便后续操作,这里采用两个HashMap管理Emoji:emojiMapHeat和emojiMapMessage。前者的键为emojiId,值为该emojiId对应emoji的热度。后者的键是emojiId,值为一个ArrayList,里面装有使用了该emojiId的EmojiMessage(此处为正确实现,笔者之前的实现有bug,后文会详述)。其余架构无太大变化。
图模型构建与维护
本次作业中图的结构保持不变。
算法及性能分析
本次作业中涉及到图论算法的方法是sendIndirectMessage,其实现就是在原有的sendMessage基础上要返回两个Person之间最短路径的长度。即这个方法涉及到最短路径算法。
最短路径算法中两个经典的算法是dijkstra算法和floyd算法。时间复杂度分别是\(O(n^2)\)和\(O(n^3)\)。显然在java语言本身比较慢且时间有限制的情况下笔者选择了前者。并且dijkstra算法也比较契合现在已经实现的架构。
dijkstra算法作为一个经典算法,关于算法的实现资料有很多,这里不再赘述。和上面的Prim算法一样,在10000条指令的限制下很可能超时,所以依旧需要进行堆优化。将时间复杂度降到\(O(nlogn)\)。最后实现的算法代码如下。
private int dijkstra(Person person1, Person person2) {
HashSet<Integer> chosenSet = new HashSet<>();
int nowId = person1.getId();
int endId = person2.getId();
HashMap<Integer, Integer> pathLength = new HashMap<>();
PriorityQueue<Relation> relations = new PriorityQueue<>(
Comparator.comparingInt(Relation::getValue)
);
chosenSet.add(nowId);
pathLength.put(nowId, 0);
while (!chosenSet.contains(endId)) {
for (Relation relation: ((SocialPerson) people.get(nowId)).getAcquaintance().values()) {
int personId = relation.getPerson().getId();
if (!chosenSet.contains(personId) &&
(!pathLength.containsKey(personId) ||
pathLength.get(personId) >
pathLength.get(nowId) + relation.getValue())) {
//被选集合中没有该点且该点之前不可达或当前路径较短,均需要更新
int newValue;
newValue = pathLength.get(nowId) + relation.getValue();
pathLength.put(personId, newValue);
relations.add(new Relation(newValue, relation.getPerson()));
}
}
Relation chosenRelation;
while (true) {
chosenRelation = relations.poll();
if (!chosenSet.contains(chosenRelation.getPerson().getId())) {
break;
}
}
nowId = chosenRelation.getPerson().getId();
chosenSet.add(nowId);
}
return pathLength.get(endId);
}
同样可以发现,这里对优先队列的维护也采用了类似上面“虚边”的机制来简化和加速整个算法的实现。而且可以从Prim和dijkstra算法的优化中可以看出,基本上需要维护最大最小值的算法都可以使用堆来进行优化。
综上,我们用堆优化的dijkstra算法实现了sendIndirectMessage中计算最短路径的功能,时间复杂度\(O(nlogn)\),符合要求。
测试
测试的方式还是和上次作业一样采用正确性测试+随机大量数据测试+极端数据测试三个层次递进的方式。
正确性测试策略不变,依旧是对照规格写JUnit测试类。由于本次作业扩展了消息的种类,且对每种消息都具有不同的处理方式。所以这里需要测试的点也比较多。比如红包消息需要判断最后发红包的和收红包的钱数对不对,并且这里群发红包的计算中用的是整除,即最后发红包那方实际扣除的钱数会小于等于指令给出的钱数(在源代码中,笔者对群发红包的消息的处理是发红包的先按组内人数\(n\)计算完每个红包的价值\(i\)后将其发给组内所有人,包括自己,然后再扣除掉发出去的钱。最后发红包的人损失的钱数也是\((n-1)\times i\),且无需在发红包过程中考虑被发对象是否是自己,简化了整个流程,这种情况下说“小于等于指令给出的钱数”是合理的),所以需要在测试时多留个心眼。除了红包之外,Notice消息的清除和emoji消息的热度增加这些都是要考虑进去进行测试的,这里不多赘述。
随即大量数据测试依旧是扩展之前的评测机即可。
极端数据测试这次笔者特意过了一遍所有的方法,确定了只有dijkstra这部分可能会超时,以防止上次作业的情况出现。同样地,针对这个算法构造极端数据的方式和之前类似,也是通过构建一幅比较复杂的图后输入大量的sim指令来进行测试。一个测试样例如下。
ap 0 0 200
ap 1 1 200
ap 2 2 200
...
ar 1 1 233
ar 1 2 456
...
am 0 485 0 0 99
sim 0
am 0 485 0 99 0
sim 0
...
可以发现一个问题,为了使sim正常执行,必须要有一条消息存在于网络中,而消息被送出后就从网络这一级删除了。所以需要加消息指令和送消息指令循环执行才能确保每次sim都能正常执行。但这样便极大地增加了指令开销,整个测试点的强度也会有所下降,目前笔者没找到能够提高这类测试点指令利用率的方法,或者说由于规格限制,这么做已经达到了指令的最大利用率。
bug情况
本次作业的强测没有bug,互测则发现了一个非常大的bug。
前面有提到,emojiId和messageId是互相独立的两套ID体系。一条emoji消息只能对应一个emojiId,但是一个emojiId是可以对应多条消息的。在规格内其实没有明说这一点,但是从addMessage的规格中我们可以推理出来。
/*@ public normal_behavior
@ requires !(\exists int i; 0 <= i && i < messages.length; messages[i].equals(message)) &&
@ (message instanceof EmojiMessage) ==> containsEmojiId(((EmojiMessage) message).getEmojiId()) &&
@ (message.getType() == 0) ==> (message.getPerson1() != message.getPerson2());
@ assignable messages;
@ ensures messages.length == \old(messages.length) + 1;
@ ensures (\forall int i; 0 <= i && i < \old(messages.length);
@ (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i]))));
@ ensures (\exists int i; 0 <= i && i < messages.length; messages[i].equals(message));
@ also
@ public exceptional_behavior
@ signals (EqualMessageIdException e) (\exists int i; 0 <= i && i < messages.length;
@ messages[i].equals(message));
@ signals (EmojiIdNotFoundException e) !(\exists int i; 0 <= i && i < messages.length;
@ messages[i].equals(message)) &&
@ (message instanceof EmojiMessage) &&
@ !containsEmojiId(((EmojiMessage) message).getEmojiId());
@ signals (EqualPersonIdException e) !(\exists int i; 0 <= i && i < messages.length;
@ messages[i].equals(message)) &&
@ ((message instanceof EmojiMessage) ==>
@ containsEmojiId(((EmojiMessage) message).getEmojiId())) &&
@ message.getType() == 0 && message.getPerson1() == message.getPerson2();
@*/
可以看到,在异常行为部分,该方法只针对emojiId不存在报了异常,并没有针对emojiId重复或emojiId已被使用之类的问题报异常,所以一个emojiId是可以对应多个emojiMessage的。但是该规格本身没有明写出来,笔者在写程序时由于惯性思维,自动“脑补”了“一个emojiId对应一条emojiMessage“这一错误的规格,将存储emoji信息的HashMap的值类型都设置成了Message(即只有一条),最后导致bug的产生。
修复bug只需要将原本用于存储emoji消息的值类型由Message改为ArrayList<Message>或LinkedList<Message>即可。
//错误实现
private final HashMap<Integer, Message> emojiMapMessage;//emojiId-emojiMessage
//正确实现
private final HashMap<Integer, ArrayList<Message>> emojiMapMessage;//emojiId-emojiMessage
这个例子便印证了我上述说过的关于JUnit的结论:JUnit高度依赖于程序员对规格的理解。按照原来的理解,再加入一条emoji消息后,JUnit测试语句会是下面这个样子。
assertTrue(emojiMapMessage.get(emojiId).equals(Message));
显然这是错误的,但是根据原有实现,这句语句能够成功执行并通过测试,最终得出”正确性测试通过“的结论。
而更改过后的实现对应的JUnit测试语句应该是下面这句。
assertTrue(emojiMapMessage.get(emojiId).contains(Message));
二者仅有细小的差别,且都能得出”测试通过“的结果,但前者是错误的,后者是正确的。原因就在于前后对规格的理解不同。
Network扩展
从需求中易得,新的这几种Person拥有原来Person的功能,同时也具有一些自己独有的功能,可以从原来的Person继承而来。而广告的实质也是一种消息,和消费者的购买消息一起可以从原有的Message继承而来。形成下图所示的类图结构。

由需求,Network此时需要具备传递广告和购买信息,查询某种商品的销售额以及销售路径的功能。而销售路径实际上与生产商和消费者在网络中所处的位置有关,因此一个商品和一对生产商、消费者对应了一条销售路径。所以除了上面涉及到的类之外,我们还需要添加一个产品类Product。
我们可以得到Network需要扩展的接口方法及解释如下。
void sendAdvertisement(int id) throws PersonIdNotFoundException, NotAdvertiserException;//发送广告消息
void addAdvertisementToAdvertiser(int id1, int id2, int id3) throws PersonIdNotFoundException, NotProducerException, NotAdvertiserException, ProductIdNotFoundException, RelationNotFoundException, NotProducutProducerException;//Producer将自己产品的广告给Advertiser
void BuyProduct(int id1, int id2) throws PersonIdNotFoundException, NotConsumerException, ProductIdNotFoundException;//Consumer消费产品
int querySaleOfProduct(int id) throws ProductIdNotFoundException;//查询商品销售额
int queryPriceOfProduct(int id) throws ProductIdNotFoundException;//查询商品单价
List<Integer> queryPathForSellingProduct(int id1, int id2, int id3) throws ProductIdNotFoundException, PersonIdNotFoundException, NotProducerException, NotConsumerException;//查询商品从Producer到Consumer的销售路径
其中方法sendAdvertisement的JML规格如下。
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < people.length; people[i].getId() == id && people[i] instanceof Advertiser);
@ ensures (Advertiser p;(\exists int i; 0 <= i && i < people.length; p == people[i] && people[i].getId() == id && people[i] instanceof Advertiser);
@ ensures (\forall int i;0 <= i && i < \old(p.advertisements.length);(\forall int j; 0 <= j && j < people.length; p.isLinked(people[j]) ==> people[j].messages.length == \old(people[j].messages.length) + 1 && (\exists int k;0 <= k && k <= people[j].messages.length; people[j].messages[k] == p.advertisements[i]))));
@ ensures (\forall int i;0 <= i && i < \old(p.advertisements.length);(\forall int j; 0 <= j && j < people.length; !p.isLinked(people[j]) ==> people[j].messages.length == \old(people[j].messages.length;
@ ensures (\forall int i;0 <= i && i < people.length;(\forall int j;0 <= j && j < \old(people[i].messages.length);(\exists int k;0 <= k && k < people[i].messages.length;\old(people[i].messages[j]) == people[i].messages[k]));
@ ensures p.advertisement.length == 0;
@ also
@ public exceptional_behavior
@ signals (PersonIdNotFoundException e) !(\exists int i; 0 <= i && i < people.length;
@ people[i].getId() == id);
@ signals (NotAdvertisementException e) (\exists int i; 0 <= i && i < groups.length;
@ people[i].getId() == id && !(people[i] instanceof Advertiser);
@*/
void sendAdvertisement(int id) throws PersonIdNotFoundException, NotAdvertiserException;
这里抛出的后一个异常是新的异常,表示传入id对应的Perosn不是Advertiser。而这里并没有处理多条同种广告的情况,原因是这样可以模拟出生产商之间的投资和竞争,一个Advertiser那拿到的同一个广告越多,表明该广告对应的Producer的投资比较大,投放广告时的条数就越多,越容易引起Consumer的注意。
而一个广告商在派发广告时肯定是一次性把手上所有的广告都派发出去最为节省成本,所以这里设计的也是一次性将广告派发给直接连接的人的做法。
addAdvertisementToAdvertiser方法的JML规格如下。
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1 && people[i] instanceof Producer);
@ requires (\exists int i; 0 <= i && i < people.length; people[i].getId() == id2 && people[i] instanceof Advertiser);
@ requires (\exists int i; 0 <= i && i < products.length; products[i].getId() == id3 && people[i] instanceof Product);
@ requires (Producer p; (\exists int i; 0 <= i && i < people.length; a == people[i] && people[i].getId() == id1 && people[i] instanceof Producer));
@ requires (Advertiser a; (\exists int i; 0 <= i && i < people.length; p == people[i] && people[i].getId() == id2 && people[i] instanceof Advertiser));
@ requires (Product pd; ((\exists int i; 0 <= i && i < products.length; pd == products[i] && products[i].getId() == id3 && people[i] instanceof Product));
@ requires p.isLinked(a);
@ requires (\exists int i;0 <= i && i < p.products.length; p.products[i] == pd);
@ ensures a.advertisements.length == \old(a.advertisements.length) + 1;
@ ensures (\exists int i;0 <= i && i < a.advertisements.length; a.advertisements[i].product == pd);
@ ensures (\forall int i;0 <= i && i < \old(a.advertisement.length);(\exists int j;0 <= j && j < a.advertisements.length;\old(a.advertisements[i]) == a.advertisements[j]));
@ also
@ public exceptional_behavior
@ signals (PersonIdNotFoundException e) !(\exists int i; 0 <= i && i < people.length;
@ people[i].getId() == id1 || people[i].getId() == id2);
@ signals (NotProducerException e) (\exists int i; 0 <= i && i < groups.length;
@ people[i].getId() == id1 && !(people[i] instanceof Producer);
@ signals (NotAdvertiserException e) (\exists int i; 0 <= i && i < groups.length;
@ people[i].getId() == id2 && !(people[i] instanceof Advertiser);
@ signals (ProductIdNotFoundException e) !(\exists int i; 0 <= i && i < products.length;
@ products[i].getId() == id3);
@ also
@ public exceptional_behavior
@ requires (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1 && people[i] instanceof Producer);
@ requires (\exists int i; 0 <= i && i < people.length; people[i].getId() == id2 && people[i] instanceof Advertiser);
@ requires (\exists int i; 0 <= i && i < products.length; products[i].getId() == id3 && people[i] instanceof Product);
@ requires (Producer p; (\exists int i; 0 <= i && i < people.length; a == people[i] && people[i].getId() == id1 && people[i] instanceof Producer));
@ requires (Advertiser a; (\exists int i; 0 <= i && i < people.length; p == people[i] && people[i].getId() == id2 && people[i] instanceof Advertiser));
@ requires (Product pd; ((\exists int i; 0 <= i && i < products.length; pd == products[i] && products[i].getId() == id3 && people[i] instanceof Product));
@ signals (RelationNotFoundException e) (p.isLinked(a) == false);
@ signals (NotProductProducerException e) !(\exists int i;0 <= i && i < p.products.length; p.products[i] == pd);
@*/
void addAdvertisementToAdvertiser(int id1, int id2, int id3) throws PersonIdNotFoundException, NotProducerException, NotAdvertiserException, ProductIdNotFoundException, RelationNotFoundException, NotProductProducerException;
其中新的几个异常分别的意思是:
-
NotProducerException:id对应的Person不是Producer -
ProductIdNotFoundException:没有该ID对应的Product -
NotProductProducerException:Product不由该Producer生产
同样地,当Producer将某个产品的广告需求发给Advertiser时,该产品并不会被删除,因为Producer完全可以将同一产品的广告投给不同的Advertiser以提升广告的效果。
BuyProduct方法的JML规格如下所示。
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1 && people[i] instanceof Consumer);
@ requires (\exists int i; 0 <= i && i < products.length; products[i].getId() == id2);
@ requires (Consumer c; ((\exists int i; 0 <= i && i < people.length; c == people[i] && people[i].getId() == id1 && people[i] instanceof Consumer));
@ requires (Product pd; (\exists int i; 0 <= i && i < products.length; pd == products[i] && products[i].getId() == id2));
@ requires (\exists int i; 0 <= i && i < c.messages.length; c.messages[i] instanceof Advertisement && ((Advertisement) c.messages[i]).product == pd);
@ requires (Advertiser a; (\exists int i; 0 <= i && i < c.messages.length; c.messages[i] instanceof Advertisement && ((Advertisement) c.messages[i]).product == p && a == c.messages[i].advertiser));
@ requires (Producer p == pd.producer);
@ requires isCircle(a.getId(), p.getId()) && isCircle(c.getId(), a.getId());
@ ensures p.messages.length == \old(p.messages.length) + 1;
@ ensures (\forall int i; 0 <= i && i < \old(p.messages.length); (\exists int j;0 <= j && j < p.messages.length; p.messages[j] == \old(p.messages.[i])));
@ ensures (\exists int i; 0 <= i && i < \old(p.messages.length); p.messages[i] instanceof BuyMessage && ((BuyMessage) p.messages[i]).consumer == c);
@ also
@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1 && people[i] instanceof Consumer);
@ requires (\exists int i; 0 <= i && i < products.length; products[i].getId() == id2);
@ requires (Consumer c; ((\exists int i; 0 <= i && i < people.length; c == people[i] && people[i].getId() == id1 && people[i] instanceof Consumer));
@ requires (Product pd; (\exists int i; 0 <= i && i < products.length; pd == products[i] && products[i].getId() == id2));
@ requires !(\exists int i; 0 <= i && i < c.messages.length; c.messages[i] instanceof Advertisement && ((Advertisement) c.messages[i]).product == pd);
@ requires (Producer p == pd.producer);
@ requires isCircle(c.getId(), p.getId());
@ ensures p.messages.length == \old(p.messages.length) + 1;
@ ensures (\forall int i; 0 <= i && i < \old(p.messages.length); (\exists int j;0 <= j && j < p.messages.length; p.messages[j] == \old(p.messages.[i])));
@ ensures (\exists int i; 0 <= i && i < \old(p.messages.length); p.messages[i] instanceof BuyMessage && ((BuyMessage) p.messages[i]).consumer == c) && ((BuyMessage) p.messages[i]).product == pd);
@ also
@ public exceptional_behavior
@ signals (PersonIdNotFoundException e) !(\exists int i; 0 <= i && i < people.length;
@ people[i].getId() == id1);
@ signals (ProductIdNotFoundException e) !(\exists int i; 0 <= i && i < products.length;
@ products[i].getId() == id2;
@ also
@ public exceptional_behavior
@ requires (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1 && people[i] instanceof Consumer);
@ requires (\exists int i; 0 <= i && i < products.length; products[i].getId() == id2);
@ requires (Consumer c; ((\exists int i; 0 <= i && i < people.length; c == people[i] && people[i].getId() == id1 && people[i] instanceof Consumer));
@ requires (Product pd; (\exists int i; 0 <= i && i < products.length; pd == products[i] && products[i].getId() == id2));
@ requires (Producer p == pd.producer);
@ signals (CannotBuyFromProducerException e) !(isCircle(c.getId(), p.getId()));
@*/
void BuyProduct(int id1, int id2) throws PersonIdNotFoundException, NotConsumerException, ProductIdNotFoundException, CannotBuyFromProducerException;
其中新的异常的意思是:
CannotBuyFromProducerException:Comsumer无法从Producer那购买产品。
可以发现,这里分了两种情况,一种是Comsumer收到广告后去买产品,这时由需求需要经过Advertiser。但现实中,大多数情况下我们不是因为看了广告才去买的产品。所以在这种情况下,我们约定Consumer直接去找Producer购买产品即可(没有中间商赚差价)。
心得与体会
本单元让我印象最深刻的应该就是JML规格化的逻辑缜密性。
初看JML规格的时候我的第一感觉其实是“略显啰嗦”,从上面的规格表述中也可看出我们需要通过大量的\forall,\exists等语句来阐明一个可能用自然语言一句话就能说清楚的事。但是随着作业的推进,我也渐渐明白这种语言上的复杂换来的是逻辑的严密。就像之前提到的有关EmojiId和MessageId的事一样。规格里从来没有明写出一个EmojiId可以对应多个MessageId。但是通过上面的推理我们可以得出这个推论。这倒让我想起下面这句话。
被允许的被允许,被禁止的被禁止,不被禁止的都被允许。
上面这句话倒是很符合JML规格语言,尤其是最后那句“不被禁止的都被允许”,表明JML作为规格语言的严谨性,就是一旦你要对某个规格作限制的话必须要点明出来。而没有被声明的部分实际上允许发生任何改变。就像上面那个例子一样。没有明文点出EmojiId和Message的关系。那么这里的对应关系就没有作出限制,此时编程人员应当遵循的是所有可能情况中最宽泛的那种(在本例中即为一个EmojiId对多个Message)以应对所有可能出现的情况。而这种思维和处理方式实际上也使得“未点明的规格”也变成了一种实实在在的约束编程的一种规格。
第三单元结束了,总体而言编程难度不算大,但是阅读量倒是很大。下个单元UML估计也是类似的。至少我不会再信说“电梯过后OO就轻松了”这种话了
标签:总结,Person,int,规格,面向对象,算法,JML,节点,单元 来源: https://www.cnblogs.com/fishlife/p/16339518.html