凸优化

目录

• 凸优化
  • Duality
    • Lagrange function（拉格朗日函数）
      • 定义
    • Lagrange duality function（拉格朗日对偶函数）
      • 定义
      • 性质
      • Lagrange duality function 和 Conjugate function（共轭函数）
        • Conjugate function 定义
        • Lagrange duality function 与 Conjugate function 的关系
    • Lagrange 对偶问题
      • 定义
      • Weak Duality (弱对偶性)
      • Strong Duality (强对偶性)
      • 强对偶性的充分条件：Slater 条件 + convex function
        • 仿射集合
        • 仿射包
        • 相对内点集
        • Slater 条件
        • 修正 Slater 条件
      • 证明Slater 条件 + convex function $ \Rightarrow $ 强对偶性
        • 支撑超平面
        • 超平面分离定理
    • 最优性条件
      • 次优解认证和终止准则
      • 互补松驰性
      • KKT 最优性条件
  • 度量拓扑
    • 内点
      • 定义
    • 开集
      • 定义
      • 性质
    • 闭集
      • 定义
      • 性质
    • 极限点
      • 定义
      • 性质
    • 导集与闭包
      • 定义
      • 性质
    • 内部
      • 定义
      • 性质

目前主要根据 Boyd, Vandenberghe, Convex Optimization来学习凸优化，因为作者理解尚浅，有些理解不足和表达不清的地方，可以在 Convex Optimization 对应知识点进行补充理解， 还请批评指正。

Duality

研究以下标准形式的优化问题，我们称之为原问题：

\[\begin{array}{*{20}{c}} {}&{\min {f_0}\left( x \right)}&{}\\ {s.t.}&{{f_i}\left( x \right) \le 0,i = 1, \ldots ,m}&{}\\ {}&{{h_i}\left( x \right) \le 0,i = 1, \ldots ,p}&{} \end{array} \tag{1} \]

其中，变量 \(x \in D\)，其中定义域 \(D= \cap_{i=0}^{m}domf_{i}\left(x\right)\cap\cap_{i=1}^{p}domh_{i}\left(x\right)\)，假设是非空集合。记原问题的最优值为 $p^{*} $。

Lagrange function（拉格朗日函数）

定义

原问题 \(\left(1\right)\) 的 Lagrange function 为：

\[L\left(x,\lambda,\nu \right)=f_{0}\left(x\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(x\right) \]

其中，定义域为 \(dom L= D \times R_{m} \times R_{p}\)，\(\lambda_{i}, \nu_{i}\) 称为第 \(i\) 个不等式约束 \({f_i}\left( x \right) \le 0\) ，第 \(i\) 个等式约束 \({h_i}\left( x \right) \le 0\) 对应的 Langrange 乘子。向量 \(\lambda,\nu\) 称为对偶变量或者是原问题 \(\left(1\right)\) 的 Lagrange 乘子向量。

Lagrange duality function（拉格朗日对偶函数）

定义

原问题 \(\left(1\right)\) 的 Lagrange duality function 为：

\[g\left(\lambda,\nu\right)=\mathop {\inf }\limits_{x \in D}L\left(x,\lambda,\nu \right)=\mathop {\inf }\limits_{x \in D}\left(f_{0}\left(x\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(x\right)\right) \]

其中，定义域为 \(dom g=R_{m} \times R_{p}\)。

性质

• Lagrange duality function 是一族关于 \(\left(\lambda,\nu\right)\) 的一族仿射函数的逐点下确界，对偶函数一定是凹函数。

Reference：

为什么拉格朗日对偶函数一定是凹函数 (逐点下确界)

证明思路：

利用凹函数定义以及 Lagrange duality function 的定义

\[g\left(\theta \lambda_{1}+\left(1- \theta \right)\lambda_{2},\theta \nu_{1}+\left(1- \theta \right)\nu_{2}\right) \geq \theta g\left(\lambda_{1},\nu_{1}\right)+\left(1- \theta \right)g\left(\lambda_{2},\nu_{2}\right) \\ g\left(\lambda,\nu\right)=min\left\{L\left(x_{1},\lambda,\nu \right),L\left(x_{2},\lambda,\nu \right),...,L\left(x_{n},\lambda,\nu \right) \right\} \]

得

\[\begin{align} & g\left( \theta {{\lambda }_{1}}+\left( 1-\theta \right){{\lambda }_{2}},\theta {{\nu }_{1}}+\left( 1-\theta \right){{\nu }_{2}} \right) \\&=min\left\{ L\left( {{x}_{1}},\theta {{\lambda }_{1}}+\left( 1-\theta \right){{\lambda }_{2}},\theta {{\nu }_{1}}+\left( 1-\theta \right){{\nu }_{2}} \right),L\left( {{x}_{2}},\theta {{\lambda }_{1}}+\left( 1-\theta \right){{\lambda }_{2}},\theta {{\nu }_{1}}+\left( 1-\theta \right){{\nu }_{2}} \right),...,L\left( {{x}_{n}},\theta {{\lambda }_{1}}+\left( 1-\theta \right){{\lambda }_{2}},\theta {{\nu }_{1}}+\left( 1-\theta \right){{\nu }_{2}} \right) \right\} \\ & \ge min\left\{ \theta L\left( {{x}_{1}},{{\lambda }_{1}},{{\nu }_{1}} \right)+\left( 1-\theta \right)L\left( {{x}_{1}},{{\lambda }_{2}},{{\nu }_{2}} \right),\theta L\left( {{x}_{2}},{{\lambda }_{1}},{{\nu }_{1}} \right)+\left( 1-\theta \right)L\left( {{x}_{2}},{{\lambda }_{2}},{{\nu }_{2}} \right),...,\theta L\left( {{x}_{n}},{{\lambda }_{1}},{{\nu }_{1}} \right)+\left( 1-\theta \right)L\left( {{x}_{n}},{{\lambda }_{2}},{{\nu }_{2}} \right) \right\} \\ & \ge \theta min\left\{ L\left( {{x}_{1}},{{\lambda }_{1}},{{\nu }_{1}} \right),L\left( {{x}_{2}},{{\lambda }_{1}},{{\nu }_{1}} \right),...,L\left( {{x}_{n}},{{\lambda }_{1}},{{\nu }_{1}} \right) \right\}+\left( 1-\theta \right)min\left\{ L\left( {{x}_{1}},{{\lambda }_{2}},{{\nu }_{2}} \right),L\left( {{x}_{2}},{{\lambda }_{2}},{{\nu }_{2}} \right),...,L\left( {{x}_{n}},{{\lambda }_{2}},{{\nu }_{2}} \right) \right\} \\ & \ge \theta g\left( {{\lambda }_{1}},{{\nu }_{1}} \right)+\left( 1-\theta \right)g\left( {{\lambda }_{2}},{{\nu }_{2}} \right) \end{align} \]

• Lagrange duality function 提供了原问题 \(\left(1\right)\) 的最优值 \(p^{*}\) 的下界，对任意 \(\lambda \geq 0\) 和 \(\nu\) 下式成立
  \[g\left(\lambda,\nu\right)\leq p^{*} \]

证明思路：

利用 Lagrange duality function 的定义，令 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)=p^{*}\) (或者设为原问题的一个可行解)，其中 \(\overset{\sim }{\mathop{x}}\in D\)。

\[\begin{equation} \begin{split} g\left(\lambda,\nu\right)&=\mathop {\inf }\limits_{x \in D}L\left(x,\lambda,\nu \right) \\&=\mathop {\inf }\limits_{x \in D}\left(f_{0}\left(x\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(x\right)\right)\\ & \leq f_{0}\left(\overset{\sim }{\mathop{x}}\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(\overset{\sim }{\mathop{x}}\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(\overset{\sim }{\mathop{x}}\right)\\ {\color{Blue}\because \lambda_{i} \geq 0,f_{i}\left(x\right) \leq 0, \therefore} &\leq f_{0}\left(\overset{\sim }{\mathop{x}}\right)\\ &=p^{*} \end{split} \end{equation} \]

Lagrange duality function 和 Conjugate function（共轭函数）

Conjugate function 定义

\(f:R^{n}\rightarrow R\)，则其共轭函数 \(f^{*}\) 为

\[f^{*}\left(y\right)=\mathop {\sup }\limits_{x \in D}\left\{ y^{T}x-f\left(x\right)\right\} \]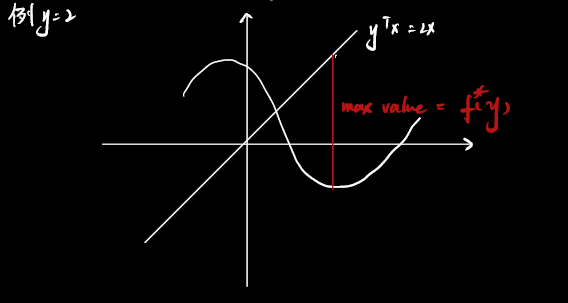

Lagrange duality function 与 Conjugate function 的关系

考虑下面优化问题

\[\begin{array}{*{20}{c}} {}&{\min {f_0}\left( x \right)}&{}\\ {s.t.}&{Ax\leq b}&{}\\ {}&{Cx=d}&{} \end{array} \tag{2} \]

可以转换为

\[\begin{array}{*{20}{c}} {}&{\min {f_0}\left( x \right)}&{}\\ {s.t.}&{Ax-b\leq 0}&{}\\ {}&{Cx-d=0}&{} \end{array} \tag{3} \]

则优化问题\(\left(3\right)\)的 Lagrange duality function

\[ \begin{align*} & g\left( \lambda ,\nu \right)=\underset{x\in D}{\mathop{\inf }}\,L\left( x,\lambda ,\nu \right) \\ & =\underset{x\in D}{\mathop{\inf }}\,\left( {{f}_{0}}\left( x \right)+{{\lambda }^{T}}\left( Ax-b \right)+{{\nu }^{T}}\left( Cx-d \right) \right) \\ & =\underset{x\in D}{\mathop{\inf }}\,\left( {{f}_{0}}\left( x \right)+{{\lambda }^{T}}Ax+{{\nu }^{T}}Cx \right)-{{\lambda }^{T}}b-{{\nu }^{T}}d \\ & =-\underset{x\in D}{\mathop{\sup }}\,-\left( {{f}_{0}}\left( x \right)+{{\lambda }^{T}}Ax+{{\nu }^{T}}Cx \right)-{{\lambda }^{T}}b-{{\nu }^{T}}d \\ & =-\underset{x\in D}{\mathop{\sup }}\,\left( {{\left( -{{A}^{T}}\lambda -{{C}^{T}}\nu \right)}^{T}}x-{{f}_{0}}\left( x \right) \right)-{{\lambda }^{T}}b-{{\nu }^{T}}d \\ & =-f_{0}^{*}\left( -{{A}^{T}}\lambda -{{C}^{T}}\nu \right)-{{\lambda }^{T}}b-{{\nu }^{T}}d \end{align*} \]

其中，下确界问题与上确界问题的等价关系为

\[\underset{x\in D}{\mathop{\inf }}\,S\left( x \right)=-\underset{x\in D}{\mathop{\sup }}\,-S\left( x \right) \]

此关系多数用于计算与证明，如果知道某些函数的共轭函数，可以很方便求对偶函数。

Lagrange 对偶问题

回顾以下两个知识点

• 原问题：

\[\begin{array}{*{20}{c}} {}&{\min {f_0}\left( x \right)}&{}\\ {s.t.}&{{f_i}\left( x \right) \le 0,i = 1, \ldots ,m}&{}\\ {}&{{h_i}\left( x \right) \le 0,i = 1, \ldots ,p}&{} \end{array} \tag{1} \]

其中，变量 \(x \in D\)，其中定义域 \(D= \cap_{i=0}^{m}domf_{i}\left(x\right)\cap\cap_{i=1}^{p}domh_{i}\left(x\right)\)，假设是非空集合。记原问题的最优值为 $p^{*} $。

• 对任意 \(\lambda \geq 0\) 以及 \(\nu\) ，Lagrange duality function 提供了原问题最优值的一个下界

\[g\left(\lambda,\nu\right)\leq p^{*} \]

既然 Lagrange duality function 能提供原问题最优值的一个下界，那很自然就能想到，最接近最优值的下界是什么？或者说最大的下界是多少？我们把求解最接近最优值的下界的问题转换成以下优化问题，并称为原问题\(\left(1\right)\)的 Lagrange 对偶问题。

定义

\[\begin{array}{*{20}{c}} {}&{\max {g\left(\lambda,\nu\right)}}&{}\\ {s.t.}&{\lambda \ge 0}&{}\tag{4} \end{array} \]

其中，变量 \(\left(\lambda,\nu\right)\in dom\text{ } g\)，假设是非空集合。记对偶问题的最优值为 $ d^{*} $。

如果 $g\left(\lambda,\nu\right) = - \infty $，即对偶问题提供一个平凡下界，这样对估计原问题的最优解意义不大。只有当 \(\lambda \ge 0\) 且 \(\left(\lambda,\nu\right)\in dom\text{ } g\)，才能提供一个非平凡下界，我们称这些 \(\left(\lambda,\nu\right)\) 是对偶可行的。如果\(\left(\lambda^{*},\nu^{*}\right)\) 是 Lagrange 对偶问题的最优解，那么称 \(\left(\lambda^{*},\nu^{*}\right)\) 是对偶最优解或者是最优Lagrange乘子。

Weak Duality (弱对偶性)

对 $ \forall \left(\lambda,\nu\right)\in dom\text{ } g$，我们有

\[\begin{equation} \begin{split} g\left(\lambda,\nu\right) \leq p^{*}\\ max \text { }g\left(\lambda,\nu\right) \leq p^{*}\\ d^{*} \leq p^{*}\\ \end{split} \end{equation} \]

！！！注意，到现在为止，我们讨论的优化问题并不局限于凸问题，例如即使原问题不是凸问题，弱对偶性仍然成立

我们把原问题的可行解 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)\) 与对偶问题的可行解 \(g\left(\lambda,\nu\right)\)之间的差值 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)-g\left(\lambda,\nu\right)\) 定义为对偶间隙，而差值 \(p^{*}-d^{*}\) 定义为最优对偶间隙。

既然原问题和对偶问题的最优值存在弱对偶性，自然就想，什么时候不等式取等号？它的充分必要条件什么？退一步，它的充分条件是什么？

Strong Duality (强对偶性)

当最优对偶间隙为零时，即下式成立时

\[d^{*} = p^{*} \]

称强对偶性成立。

强对偶性的充分条件：Slater 条件 + convex function

先介绍几个定义

仿射集合

我们把具有这样形式的线性组合 \(\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{k}x_{k}\)，其中 \(\theta_{1}+\theta_{2}+...+\theta_{k}=1\) 称为 \(x_{1}+x_{2}+...+x_{k}\) 的仿射组合。如果集合\(C\) 包含其中任意点（包括两个点的情况）的放射组合，称该集合 \(C\) 为仿射集合，即 \(\forall x_{1},x_{2},...,x_{k} \in C\)，\(\theta_{1},\theta_{2},...,\theta_{k}\in R\)，且 \(\theta_{1}+\theta_{2}+...+\theta_{k}=1 \)，有 \(\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{k}x_{k}\in C\)。

仿射集合还可以用子空间表示，如果 \(C\) 是一个仿射集合，\(x_{0}\in C\)，则集合

\[V = C-x_{0} =\left\{x-x_{0}|x\in C\right\} \]

为子空间。

证明思路

对 \(\forall v_{1},v_{2}\in V\)，\(\forall\alpha,\beta\in R\)，有 \(v_{1}+x_{0},v_{2}+x_{0} \in C\)

\[\begin{equation} \begin{split} \alpha v_{1}+\beta v_{1}+x_{0}=\alpha \left(v_{1}+x_{0}\right)+\beta \left(v_{2}+x_{0}\right)+\left(1-\alpha-\beta\right)x_{0}&\Rightarrow \alpha v_{1}+\beta v_{1}+x_{0}\in C\\ &\Rightarrow \alpha v_{1}+\beta v_{1}\in C-x_{0}\\ &\Rightarrow \alpha v_{1}+\beta v_{1}\in V\\ \end{split} \end{equation} \]

那么 \(C\) 可以表示为

\[C = V + x_{0} =\left\{v+x_{0}|v\in V\right\} \]

仿射包

我们称由集合 \(C \subseteq R^{n}\) 中的点的所有仿射组合组成的集合为 \(C\) 的仿射包，记为 \(aff \text{ }C\)：

\[C = \left\{\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{k}x_{k}|\forall x_{1},x_{2},...,x_{k} \in C,\theta_{1}+\theta_{2}+...+\theta_{k}=1 \right\} \]

\(aff \text{ }C\) 是包含 \(C\) 的最小的仿射集合。也就是说：如果 \(S\) 是满足 \(C \subseteq S\) 的仿射集合，那么 \(aff \text{ }C\subseteq S\)

相对内点集

我们定义集合 \(D\) 的相对内部为 \(D\) 的仿射包 \(aff \text{ }D\) 的内部，即

\[relint \text{ }D =\left\{x \in D|\exists r >0,s.t.B\left(x,r\right)\cap aff\text{ }D \subseteq D\right\} \]

集合 \(D\) 的相对边界为 \(cl\text{ }D\setminus relint \text{ }D\)，其中 \(cl\text{ }D\) 表示 \(D\) 的闭包。

Slater 条件

存在一点 \(x \in relint \text{ }D\)，使得不等式约束严格成立。

\[\begin{split} \exist x \in relint \text{ }D,s.t. f_{i}(x)&<0,i=1,...,m\\ h_{i}(x)&=0,i=1,...,p \end{split} \]

修正 Slater 条件

当不等式约束函数 \(f_{i}\left(x\right)\) 中有一些仿射函数时，Slater 条件可以进一步弱化。

\[\begin{equation} \begin{split} \exist x \in relint \text{ }D,s.t. f_{i}(x)&\leq 0,i=1,...,k,f_{i}\left(x\right)\text{为仿射函数} \\f_{i}(x)&<0,i=k+1,...,m,f_{i}\left(x\right)\text{为非线性函数} \\h_{i}(x)&=0,i=1,...,p \end{split} \end{equation} \]

则强对偶性的充分条件：（修正）Slater 条件 + convex function

证明Slater 条件 + convex function $ \Rightarrow $ 强对偶性

证明之前，介绍以下定义和定理是有必要的。

支撑超平面

设 \(C \subseteq R^{n}\) 而 \(x_{0}\) 是其边界 $ bd \text{ }C$ 上的一点，即

\[x_{0} \in bd \text{ }C=cl\text{ }C\setminus int \text{ }C \]

如果 \(a \neq 0\)，并且对任意 \(x \in C\) 满足 \(a^{T}x \leq a^{T}x_{0}\) 或 \(a^{T}x \geq a^{T}x_{0}\)，那么称超平面 \(\left\{ x | a^{T}x = a^{T}x_{0}\right\}\) 为集合 \(C\) 在点 \(x_{0}\) 处的支撑超平面。

超平面分离定理

该定理主要想法就是，用超平面或仿射函数将两个不相交的集合分离开来。假设 \(C\) 和 \(D\) 是两个不相交的凸集分离开来，即 \(C \cap D = \varnothing\)，那么存在 \(a \neq 0\) 和 \(b\) 使得对于所有 \(x \in C\) 有 \(a^{T}x \leq b\)，对于所有 \(x \in D\) 有 \(a^{T}x \geq b\)。则超平面 \(\left\{ x | a^{T}x = a^{T}x_{0}\right\}\) 称为集合 \(C\) 和 \(D\) 的分离超平面。

除此之外，定义两个集合

\[g=\left\{ \underbrace{\left( {{f}_{1}}\left( x \right),...,{{f}_{m}}\left( x \right) \right)}_{u},\underbrace{\left( {{h}_{1}}\left( x \right),...,{{h}_{p}}\left( x \right) \right),}_{u}\underbrace{{{f}_{0}}\left( x \right)}_{t}|x\in D \right\} \]

\[\begin{equation} \begin{split} \Alpha =\{\left( u,v,t \right)|\exists x\in D,{{f}_{0}}\left( x \right)&\le {{u}_{i}},i=1,...,m\\ {{h}_{i}} \left( x \right)&\le {{v}_{i}},i=1,...,p,\\ {{f}_{0}} \left ( x \right)&\le t\} \in g +\left(R_{+}^{m} \times \left\{0\right\} \times R_{+}^{p}\right) \end{split} \end{equation} \]

证明思路

假设 \(rank \text{ }A = p\) ，令 \(B=\left\{ \left( 0,0,s \right)\in {{R}^{m}}\times {{R}^{n}}\times R|s<{{p}^{*}} \right\}\)

假设 \(\left( u,v,t \right) \in A \cap B\) ，第一步证明 \(A\) 和 \(B\) 是两个不相交的集合，引入分离超平面

由

\[\begin{equation} \begin{split} \left( u,v,t \right) \in B &\Rightarrow u=0, v=0, \color{Blue}{t<p^{*}}\\ \left( u,v,t \right) \in A &\Rightarrow \exists x\in D,{{f}_{i}}\left( x \right)\le {{u}_{i}}=0,{{h}_{i}}\left( x \right)=0,\color{Blue}{{{f}_{0}}\left( x \right)=t\ge {{p}^{*}}} \end{split} \end{equation} \]

蓝色部分说明 \(A\) 和 \(B\) 是两个不相交的集合。

根据超平面分离定理，存在分离超平面 \(\left( \widetilde{\lambda },\widetilde{\nu },\mu \right)\) ，使得

\[\begin{equation} \begin{split} \exists \left( \widetilde{\lambda },\widetilde{\nu },\mu \right)\ne 0,\alpha \in R\\ {\color{red}\forall\left( u,v,t \right) \in A } &{\color{red}\Rightarrow \left( \widetilde{\lambda },\widetilde{\nu },\mu\right) ^{T} \left( u,v,t \right) \geq \alpha}\\ &{\color{red}\Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)+\mu f_{0}\left(x\right) \geq \alpha}\\ {\color{green}\forall\left( u,v,t \right) \in B} &{\color{green}\Rightarrow \left( \widetilde{\lambda },\widetilde{\nu },\mu \right) ^{T} \left( u,v,t \right) \leq \alpha}\\ &{\color{green}\Rightarrow \mu t\leq \alpha} \end{split} \end{equation} \]

第二步在原问题定义域 \(g\) 上构造拉格朗日函数

对于 \(\forall \beta>1,\forall\left( u,v,t \right) \in A ,\exist \left( \beta u,v,\beta t \right)\in A,\left( \widetilde{\lambda },\widetilde{\nu },\mu \right) ^{T} \left( \beta u,v,\beta t \right) \geq \alpha\)，若 \(\widetilde{\lambda }\) 或 \(\mu <0\)，由 \(\beta\) 的无穷大性质，显然可知上述不等式不成立。所以 \(\widetilde{\lambda }\geq 0,\mu \geq0\)。

由 \({\color{green}\forall\left( u,v,t \right) \in B \Rightarrow \mu t\leq \alpha}\) 可知，对所有 \(t<p^{*}\)，都有 \(\mu t\leq \mu p^{*}\)，同时

\[\mu t\leq \mu p^{*}\leq\alpha \]

所以我们可以得到 \(\mu p^{*}\leq\alpha\)。

对 \(\forall\left( u,v,t \right) \in A\)，根据 \(\mu p^{*}\leq\alpha\) ，假设 \(\mu > 0\)（后面会证明一定成立）

\[\begin{equation} \begin{split} {\color{red}\forall\left( u,v,t \right) \in A } &{\color{red}\Rightarrow \left( \widetilde{\lambda },\widetilde{\nu },\mu\right) ^{T} \left( u,v,t \right) \geq \alpha}\\ &{\color{red}\Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)+\mu f_{0}\left(x\right) \geq \alpha}\\ &\Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)+\mu f_{0}\left(x\right) \geq \mu p^{*}\\ &\Rightarrow \sum_{i=1}^{m}\frac{\widetilde{\lambda }_{i}}{\mu}f_{i}\left(x\right)+\sum_{i=1}^{p}\frac{\widetilde{\nu }_{i}}{\mu}h_{i}\left(x\right)+f_{0}\left(x\right) \geq p^{*}\\ 令L\left(x,\frac{\widetilde{\lambda }_{i}}{\mu},\frac{\widetilde{\nu }_{i}}{\mu}\right)=L\left(x,\lambda,\nu\right)&\Rightarrow L\left(x,\lambda,\nu\right) \geq p^{*}\\ \end{split} \end{equation} \]

因为 \(g \subset A\)，在原问题定义域 \(g\) 上的拉格朗日函数 \(L\left(x,\lambda,\nu\right)=L\left(x,\frac{\widetilde{\lambda }_{i}}{\mu},\frac{\widetilde{\nu }_{i}}{\mu}\right)\geq p^{*}\)，对 \(x\) 取极小值，我们有 \(g\left(\lambda,\nu\right)=\mathop {\inf }\limits_{x \in D}L\left(x,\lambda,\nu\right)\geq p^{*}\)

第三步证明强对偶性成立

由弱对偶性，

\[g\left(\lambda,\nu\right) \leq p^{*} \]

所以

\[g\left(\lambda,\nu\right) = p^{*} \]

第四步证明 \(\mu > 0\)，这里运用到slater 条件

若 \(\mu = 0\)，假设 \(\widetilde{x}_{0}\in D\) 为满足 slater 条件的一点，所以

\[\begin{equation} \begin{split} {\color{red}\sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(\widetilde{x}_{0}\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(\widetilde{x}_{0}\right)+\mu f_{0}\left(\widetilde{x}_{0}\right) }&\geq 0\\ (\mu=0) \Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(\widetilde{x}_{0}\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(\widetilde{x}_{0}\right)&\geq 0\\ (\widetilde{x}_{0}\in D 为满足 slater 条件的一点,h_{i}\left(\widetilde{x}_{0}\right)=0) \Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(\widetilde{x}_{0}\right)&\geq 0\\ (\widetilde{x}_{0}\in D 为满足 slater 条件的一点,f_{i}\left(\widetilde{x}_{0}\right)<0,\widetilde{\lambda }_{i}\geq 0) \Rightarrow \widetilde{\lambda }_{i}&= 0 \end{split} \end{equation} \]

由于 \(\left( \widetilde{\lambda },\widetilde{\nu },\mu \right)\ne 0\)，所以 \(\widetilde{\nu }\ne 0\)。对于 \(x\in D\)，有

\[\begin{equation} \begin{split} {\color{red}\sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)+\mu f_{0}\left(x\right) }&\geq 0\\ \sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)&\geq 0\\ \widetilde{\nu }^{T}\left(Ax-b\right)&\geq 0 \end{split} \end{equation} \]

又因为 \(\widetilde{x}_{0}\in D\) 为满足 slater 条件的一点，且 \(\widetilde{x}_{0}\in int \text{ }D\)，所以

\[\exists \varepsilon ,x=\widetilde{x}_{0}-\varepsilon A^T\widetilde{\nu }\in D,s.t.\widetilde{\nu }^T(A(\widetilde{x}_{0}-\varepsilon A^T\widetilde{\nu })-b)＝-\varepsilon \widetilde{\nu }^TAA^T\widetilde{\nu }\leq0 \]

除非 \(A^{T}\widetilde{\nu } =0\) ，不然总存在 \(D\) 中的点使得 \({\widetilde{\nu }^{T}}\left( Ax-b \right)<0\)。而 \(A^{T}\widetilde{\nu }=0\left(\widetilde{\nu } \ne 0\right)\) 显然与假设 \(rank \text{ }A = p\) 矛盾。

Reference：

证明四 强对偶定理（Strong Duality Theorem） - 知乎 (zhihu.com)

最优性条件

次优解认证和终止准则

回顾以下对偶间隙的定义，我们把原问题的可行解 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)\) 与对偶问题的对偶可行解 \(g\left(\lambda,\nu\right)\)之间的差值 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)-g\left(\lambda,\nu\right)\) 定义为对偶间隙，而差值 \(p^{*}-d^{*}\) 定义为最优对偶间隙。但我们并不知道为什么引入对偶间隙这个概念。实则对偶间隙提供了我们估计可行解 $ f_{0}\left(\overset{\sim }{\mathop{x}}\right)$ 与最优值 \(p^{*}\) 差值的一个有效手段，这是因为

\[\begin{equation} \begin{split} p^{*}&\geq L\left(x,\lambda,\nu \right)\\ &\geq \mathop {\inf }\limits_{x \in D}L\left(x,\lambda,\nu \right)\\ &= g\left(\lambda,\nu\right)\\ \\ \Rightarrow f_{0}\left(\overset{\sim }{\mathop{x}}\right)-p^{*}&\leq f_{0}\left(\overset{\sim }{\mathop{x}}\right)- g\left(\lambda,\nu\right) \end{split} \end{equation} \]

可以看到，不等式右边为对偶间隙。一对原对偶问题的可行点 \(x\)，\(\left(\lambda,\nu\right)\) 将原问题（对偶问题）的最优值限制在一个区间上：

\[p^{*}\in\left [ g\left(\lambda,\nu\right), f_{0}\left(x\right)\right],d^{*}\in\left [ g\left(\lambda,\nu\right), f_{0}\left(x\right)\right] \]

因此，这一特性可用于迭代求解的终止条件。

设 \(x_{k}\) 为第 \(k\) 轮迭代的原问题可行解，\(\left(\lambda_{k},\nu_{k}\right)\) 为第 \(k\) 轮迭代的对偶可行解，\(k=1,2,...\)，给定要求的绝对精度 \(\varepsilon_{abs}>0\)，那么终止条件为：

\[f_{0}\left(x_{k}\right)- g\left(\lambda_{k},\nu_{k}\right)\leq \varepsilon_{abs} \]

考虑到量纲问题，还可以定义相对误差：

\(if \text{ }g\left(\lambda_{k},\nu_{k}\right)>0:\)

\[\frac{f_{0}\left(x_{k}\right)- p^{*}}{\left |p^{*} \right |}\leq \frac{f_{0}\left(x_{k}\right)- g\left(\lambda_{k},\nu_{k}\right)}{g\left(\lambda_{k},\nu_{k}\right)}\leq \varepsilon_{abs}\\ \]

\(if \text{ } f_{0}\left(x_{k}\right)<0:\)

\[\frac{f_{0}\left(x_{k}\right)- p^{*}}{\left |p^{*} \right |}\leq \frac{f_{0}\left(x_{k}\right)- g\left(\lambda_{k},\nu_{k}\right)}{-f_{0}\left(x_{k}\right)}\leq \varepsilon_{abs}\\ \]

如果原对偶可行对 \(x\)，\(\left(\lambda,\nu\right)\) 的对偶间隙为零，即 \(f_{0}\left(x\right)= g\left(\lambda,\nu\right)\) ，那么 \(x\) 是原问题最优解且\(\left(\lambda,\nu\right)\) 是对偶问题最优解。

可能会有一点疑惑，为什么对偶间隙为零，就是 \(x\)，\(\left(\lambda,\nu\right)\) 就是各自问题的最优解？

我们用反证法，假设 \(x\) 不是原问题最优解，即存在 \(x^{*}\)，使得 \(g\left(\lambda,\nu\right) = f_{0}\left(x\right) > f_{0}\left(x^{*}\right)\)，但由弱对偶性，显然矛盾。同理假设 \(\left(\lambda,\nu\right)\) 不是对偶问题最优解也同样成立。

互补松驰性

由弱对偶性可以得到原问题最优值的一个下界，那我们研究强对偶性，它能得到什么结论或信息？这就是互补松驰性的来源。

\[\lambda_{i}^{*}f_{i}^{*}\left(x\right)=0,i=1,...,m \]

证明思路：

有强对偶性 \(p^{*}=d^{*}\) 可得 \(f_{0}\left(x^{*}\right)=g\left(\lambda^{*},\nu^{*}\right)=L\left(x^{*},\lambda^{*},\nu^{*}\right)\)。这是因为

\[\begin{align*} & g\left( {{\lambda }^{*}},{{\nu }^{*}} \right)=f_{0}^{*}\left( {{x}^{*}} \right) \\ & \ge \underset{\lambda ,\nu }{\mathop{\max }}\,\left( {{f}_{0}}\left( {{x}^{*}} \right)+\sum\limits_{i=1}^{m}{{{\lambda }_{i}}}{{f}_{i}}\left( {{x}^{*}} \right)\left( \le 0 \right)+\sum\limits_{i=1}^{p}{{{\nu }_{i}}}{{h}_{i}}\left( {{x}^{*}} \right) \right) \\ & =\underset{\lambda ,\nu }{\mathop{\max }}\,L\left( {{x}^{*}},\lambda ,\nu \right) \\ & \ge {{f}_{0}}\left( {{x}^{*}} \right)+\sum\limits_{i=1}^{m}{\lambda _{i}^{*}}{{f}_{i}}\left( {{x}^{*}} \right)+\sum\limits_{i=1}^{p}{\nu _{i}^{*}}{{h}_{i}}\left( {{x}^{*}} \right) \\ & \ge inf\text{ }L\left( x,{{\lambda }^{*}},{{\nu }^{*}} \right) \\ & \ge g\left( {{\lambda }^{*}},{{\nu }^{*}} \right) \end{align*} \]

由不等式两边，可以得到

\[\begin{equation} \begin{split} \color{red}{g\left(\lambda^{*},\nu^{*}\right)} &= f_{0}\left(x^{*}\right)\\ &= \mathop {\max }\limits_{\lambda,\nu}\left(f_{0}\left(x^{*}\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(x^{*}\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(x^{*}\right)\right)\\ &= \mathop {\max }\limits_{\lambda,\nu}L\left(x^{*},\lambda,\nu \right)\\ &= \color{red}{f_{0}\left(x^{*}\right)+\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}\left(x^{*}\right)+\sum_{i=1}^{p}\nu_{i}^{*}h_{i}\left(x^{*}\right)}\\ &= inf \text{ }L\left(x,\lambda^{*},\nu^{*}\right)\\ &= g\left(\lambda^{*},\nu^{*}\right) \end{split} \end{equation} \]

即

\[f_{0}\left(x^{*}\right)=g\left(\lambda^{*},\nu^{*}\right)=L\left(x^{*},\lambda^{*},\nu^{*}\right)=f_{0}\left(x^{*}\right)+{\color{red}\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}\left(x^{*}\right)}+\sum_{i=1}^{p}\nu_{i}^{*}h_{i}\left(x^{*}\right) \]

所以

\[\sum_{i}^{m}\lambda_{i}^{*}f_{i}^{*}\left(x\right)=0\\ \Rightarrow\lambda_{i}^{*}f_{i}^{*}\left(x\right)=0,i=1,...,m \]

KKT 最优性条件

KKT 最优性条件如下

\[\begin{equation} \begin{split} f_{i}^{*}\left(x\right)&\leq0,i=1,...,m\\ h_{i}^{*}\left(x\right)&\leq0,i=1,...,p\\ \lambda_{i}^{*}&\geq0,i=1,...,m\\ \lambda_{i}^{*}f_{i}^{*}\left(x\right)&=0,i=1,...,m\\ \bigtriangledown f_{0}\left ( x^{*} \right )+\sum_{i}^{m}\lambda_{i}^{*}\bigtriangledown f_{i}\left(x^{*}\right)+\sum_{i}^{p}\nu_{i}^{*}\bigtriangledown h_{i}\left(x^{*}\right)&=0\\ \end{split} \end{equation} \]

• 强对偶条件 \(p^{*}=d^{*}\)，\(f_{i}\)，\(h_{i}\) 可微 \(\Rightarrow\) KKT 条件

证明思路

由强对偶条件，显然得到

\[\begin{equation} \begin{split} f_{i}^{*}\left(x\right)&\leq0,i=1,...,m\\ h_{i}^{*}\left(x\right)&\leq0,i=1,...,p\\ \lambda_{i}^{*}&\geq0,i=1,...,m\\ \lambda_{i}^{*}f_{i}^{*}\left(x\right)&=0,i=1,...,m \end{split} \end{equation} \]

又因为

\[\begin{equation} \begin{split} g\left(\lambda^{*},\nu^{*}\right)&=L\left(x^{*},\lambda^{*},\nu^{*}\right)\\ &=inf \text{ }L\left(x,\lambda^{*},\nu^{*}\right) \end{split} \end{equation} \]

若满足 \(g\left(\lambda^{*},\nu^{*}\right)=inf \text{ }L\left(x,\lambda^{*},\nu^{*}\right)\)，需要满足 \(L^{'}\left(x^{*}\right) = 0\)，即

\[\bigtriangledown _{x^{*}} L = \bigtriangledown f_{0}\left ( x^{*} \right )+\sum_{i}^{m}\lambda_{i}^{*}\bigtriangledown f_{i}\left(x^{*}\right)+\sum_{i}^{p}\nu_{i}^{*}\bigtriangledown h_{i}\left(x^{*}\right)=0 \]

• KKT 条件， \(f_{i}\)，\(h_{i}\) 可微 + 凸问题 \(\Rightarrow\) 强对偶条件 \(p^{*}=d^{*}\)

从 KKT 条件可知，\(x^{*}\) 是原问题的可行解，现证明为最优解：

由KKT 条件中 \(\bigtriangledown _{x^{*}} L = \bigtriangledown f_{0}\left ( x^{*} \right )+\sum_{i}^{m}\lambda_{i}^{*}\bigtriangledown f_{i}\left(x^{*}\right)+\sum_{i}^{p}\nu_{i}^{*}\bigtriangledown h_{i}\left(x^{*}\right)=0\) 以及凸问题，可以得到 \(x^{*}\) 是最小值。

又因为 KKT 条件 \(\lambda_{i}^{*}f_{i}^{*}\left(x\right)=0,i=1,...,m\) 可以得到

\[\begin{equation}\begin{split} g\left(\lambda^{*},\nu^{*}\right)&=L\left(x^{*},\lambda^{*},\nu^{*}\right)\\ &=f_{0}\left(x^{*}\right)+\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}\left(x^{*}\right)+\sum_{i=1}^{p}\nu_{i}^{*}h_{i}\left(x^{*}\right)\\ &=f_{0}\left(x^{*}\right) \end{split} \end{equation} \]

综上所述，强对偶条件 \(p^{*}=d^{*}\)

度量拓扑

内点

定义

设 \(\left(X,d\right)\) 是度量空间，\(G\) 是 \(X\) 的子集，若存在某个开球 \(U\left(x_{0},r\right)\)，使得 \(U\left(x_{0},r\right)\subset G\)，那么称 \(x_{0} \in G\) 称为 \(G\) 的内点。

开集

定义

若 \(G\) 的每一个点都是 \(G\) 的内点，称 \(G\) 为开集。

性质

• 任意个开集的并集是开集
• 有限个开集的交集是开集

闭集

定义

设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，若 \(F\) 的余集 \(F^{c}\) 是开集，称 \(F\) 为闭集。

性质

• \(\varnothing\) 和 \(X\) 是闭集
• 任意个闭集的交集是闭集
• 有限个闭集的并集是闭集

证明思路——利用De Morgen 公式

若 \(\left\{A_{\alpha}:\alpha\in\Lambda\right\}\) 是一族集合，则

（1）\(\left(\cup_{\alpha\in\Lambda}A_{\alpha}\right)^{c}=\cap_{\alpha\in\Lambda}A_{\alpha}^{c}\)

（2）\(\left(\cap_{\alpha\in\Lambda}A_{\alpha}\right)^{c}=\cup_{\alpha\in\Lambda}A_{\alpha}^{c}\)

极限点

定义

设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，\(x \in X\) ，若包含 \(x\) 的任意开集都含有不同于 \(x\) 的 \(F\) 的点，则称 \(x\) 为 \(F\) 的极限点。

性质

设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，\(x_{0} \in X\) ，则下列条件等价：

• \(x_{0}\) 为 \(F\) 的极限点
• 包含 \(x_{0}\) 任何一个开集都含有 \(F\) 异于 \(x_{0}\) 的无穷多个点（若有限，则在有限个点中取半径 \(min \text{ }d\) 的开球，不满足极限点定义）
• 在 \(F\) 中存在序列 \(x_{n}\)， \(x_{n}\neq x_{0}\)，且 \(\lim_{n\rightarrow \infty }x_{n} = x_{0}\)（注意，一定是 \(x_{n}\neq x_{0}\)，因为极限点要求任意开集都含有不同于 \(x_{0}\) 的点）

导集与闭包

定义

设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，称 \(F\) 的极限点全体为 \(F\) 的导集，记为 \(F^{’}\) 。\(\bar{F}=F\cup F^{'}\) 称为 \(F\) 的闭包。

性质

1. 下列条件等价：

• \(F\) 是闭集
• \(F^{’} \subset F\)
• \(\bar{F} = F\)

2. 设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，\(x \in X\) ，则下列条件等价：

• \(x \in \bar{F}\)

• \(x\) 的每个开球都包含有 \(F\) 的点

• 存在序列 \(\left\{x_{n}\right\}\)，使得 \(\lim_{n\rightarrow \infty }x_{n} = x_{0}\)（注意，这时不一定是 \(x_{n}\neq x_{0}\)，因为闭包包括\(F\) 本身的点）

内部

定义

设 \(\left(X,d\right)\) 是度量空间，\(G\) 是 \(X\) 的子集，称 \(G\) 的内点全体为 \(G\) 的内部，记为 \(G^{0}\) 。

性质

下列条件等价：

• \(G\) 是开集当且仅当 \(G^{0}=G\)
• \(G^{0}\subseteq G \subseteq \bar G\)（第一个关系 \(G^{0}\subseteq G\)，是因为 \(G\) 可能包含孤立点；第一个关系 \(G \subseteq \bar G\)，是因为 \(\bar G\) 包含了极限点（更形象去理解为边界点，因为内点也是极限点）
• 当 \(G \subset F\) 时，一定有 \(G^{0} \subset F^{0}\)，\(\bar G\ \subset \bar F\)

Reference

黎永锦.泛函分析讲义[M].北京：科学出版社，2011：6-10

标签：right,Duality,Optimization,widetilde,Convex,theta,lambda,nu,left
来源： https://www.cnblogs.com/guanyang/p/16287060.html