1.1.6.3 排序
作者:互联网
6.3 排序
内容导视:
- 时间复杂度
- 空间复杂度
- 冒泡排序
- 简单选择排序
- 直接插入排序
我们知道了如何定义数组来存放元素,那就试试对数组中的元素排序吧。
排序:一组元素按指定顺序排列的过程。生活中,排序无处不在,我会依次介绍,默认顺序:从小到大排。
对于初学者,只需要了解冒泡排序与简单选择排序、直接插入排序,其它不用看,因为大部分人不可能一次学会;如果是天才当我没说。(怨念~_~)
排序算法分为:
-
交换排序
- 冒泡排序
- 快速排序
-
选择排序
- 简单选择排序
- 堆排序
-
插入排序
- 直接插入排序
- 希尔排序
-
归并排序
-
基数排序
在完成功能的情况下,我们需要考虑如何让程序运行时间更短,占用空间更小。(你也不希望软件卡半天没响应,又特别占用内存,对吧)
由此引申出来时间复杂度与空间复杂度,接下来一一介绍。
6.3.1 时间复杂度
描述了解决特定问题的步骤称为算法,如排序算法解决了元素无序的问题。只不过在计算机上,可以使用代码描述。
解决问题的方法有多种,不同算法的效率有高有低;最直观的方法就是编写不同的程序实现不同的算法,然后输入不同数据,进行编译,运行时对它们进行计时,用时最短的就是最好的。但这种事后测量的方法有很大的缺点与不确定性:
- 实现不同程序需要耗费大量时间,而我们只需保留其中之一。
- 数据的不同,可能对某个算法更加有利;如使用顺序与逆序查找,如果查找的数就在开头,顺序唰的一下找到了,就能说明顺序一定比逆序好吗?如何选择测试数据以及数据量的多少,才能能够保证结果的公平性,很难判断的。
- 在不同的运行环境、硬件性能情况下得到的结果可能相差会很大;即使在同台机器上,也有可能测试时 CPU 负荷突然过高、运行内存忽高忽低、计算机电量不足...代码运行速度慢了下来,你究竟要测试几次,在不同的机器上,配置一个怎么样的的环境,才能得出令人信服的结果?
这时就需要我们自己在编写程序前,能够粗略估计代码的运行时间。(事前分析估算方法)
语句执行次数
也称语句频度、时间频度,记为 T(n),n 代表数据的个数。假设运行一行基础代码就算执行一次语句。代码花费的时间与语句执行次数成正比例,执行的语句越多,花费时间越多。
求 m1 方法内语句执行次数:
public static void m1(int[] arr) {
System.out.println("你好");// 执行 1 次
System.out.println("我饿了");// 执行 1 次
}
T(n) = 2;
此时数组中元素的个数 n 不会对语句执行次数产生影响,也就是说无论 arr.length 有多大,语句执行次数也就是 2。
求 for 内的语句执行次数:
public static void m2(int[] arr) {
int n = arr.length;
// 从 0 到 n - 1,一共循环 n 次,每次循环执行 2 个语句
for (int i = 0; i < n; i++) {
System.out.println("我不想排序");// 一共执行 n 次
System.out.println("我想睡觉");// 一共执行 n 次
}
}
T(n) = 2n;
求 for 内的语句执行次数:
public static void m3(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i *= 2) {
System.out.println("没想到吧");
System.out.println("还有乘等");
}
}
for 循环执行了几次?
每次循环 i *= 2
第 1 次循环 i = 1 = 20;
第 2 次循环 i = 2 = 21;
第 3 次循环 i = 4 = 22;
...
第 x+1 次循环 i = 2x;
假设第 x+1 次循环时,i >= n,不满足条件,退出循环,得出不等式:
2x >= n
解出:x >= log2n
第 log2n + 1 次循环时,i 正好等于 n,退出了循环,这次不算,那么一共执行了 log2n 次循环,每次循环时执行 2 个语句。
T(n) = 2 * log2n;
若循环次数不是整数,向上取整,如 2.321928 记作 3。
求方法中输出语句的执行次数:
public static void m4(int[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println("i=" + i
+ ",j=" + j);
}
}
}
外层 for 一共循环 n 次,里层 for 一共循环 n 次,里面的输出语句被执行了 n * n 次。
T(n) = n2;
有了语句执行次数的函数,难道就能比较不同代码的运行时间吗?
比如 T(n) = 100n + 1 与 T(n) = n2 + 7,依然无法清晰看出谁的运行时间更短,此时需要看运行时间如何随 n 的增长而变化,选出增速最小的算法。
引出渐进时间复杂度(asymptotic time complexity)这个概念:
渐进时间复杂度
简称时间复杂度,定义如下:
代码执行语句次数记作 T(n);存在函数 f(n),当 n 趋近无穷大时,T(n) / f(n) 的比值为一个不等于 0 的常数,说明 f(n) 与 T(n) 的增长率相同,是同一量级;如 \(\lim\limits_{x \to \infty} \frac{2n + 10}{n}\) = 2。
记作 T(n) = O( f(n) ),称 O( f(n) ) 为代码的时间复杂度;时间复杂度描述了代码执行时间随数据量增长的变化趋势。
如何推出 f(n)?
| 次数 n | a:2n + 10 | a`:n | b:2n2 + 5 | b`:n2 |
|---|---|---|---|---|
| 1 | 12 | 1 | 7 | 1 |
| 100 | 210 | 100 | 20005 | 10000 |
| 10000 | 20010 | 10000 | 200000005 | 100000000 |
| 1000000 | 2000010 | 1000000 | 2000000000005 | 1000000000000 |
当 n 越来越大时,常数、低次数项已经变得不太重要,如同 a 再怎么努力,也追不上 b,因此被可以省略。
- 如果函数是常数,使用 1 代替
- 若不是常数,只保留最高次数的那一项,并去除最高次数的系数
如 T(n) = 20,记作 T(n) = O(1);
T(n) = 2 * log2n + 98 = 2 * log2k * logkn + 98,只保留最高次数那项,且去掉系数,记作 T(n) = O(logkn);
设 k 为任意常数,由换底公式得:log2n = log2k * logkn
T(n) = 2n2 + 3n + 9,记作 T(n) = O(n2)。
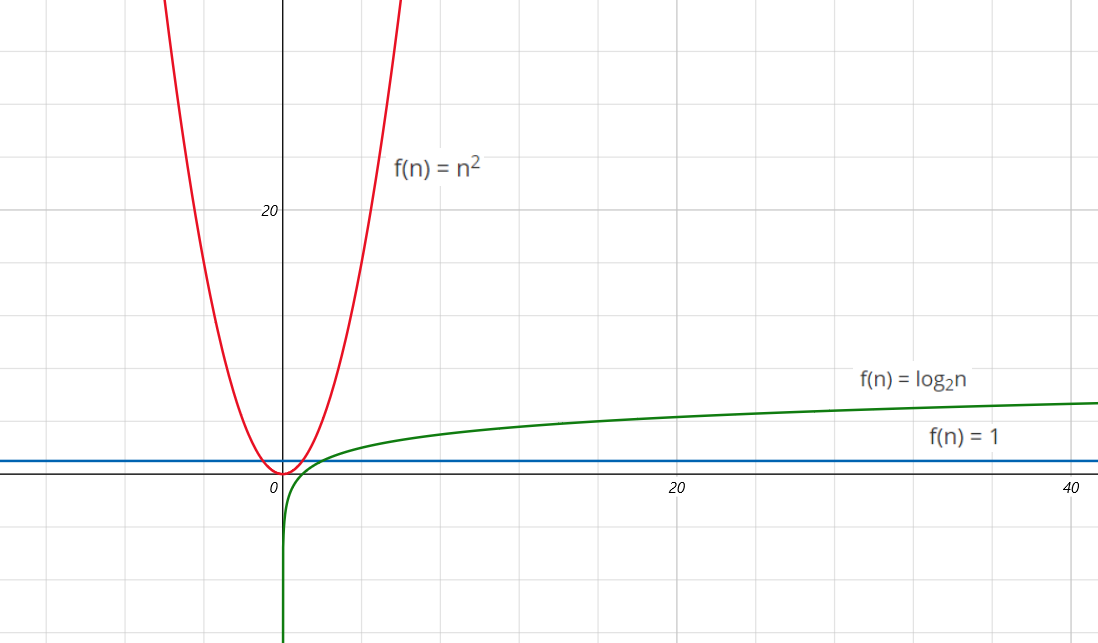
很明显随着 n 的增大,O(n2) 的时间复杂度(增长速度)远大于其它两个。
常见的时间复杂度
从小到大排(n 趋向无穷大时):
常数时间:O(1)
对数时间:O(logkn)
线性时间:O(n)
线性对数时间:O(n * logkn)
平方时间:O(n2)
立方时间:O(n3)
指数时间:O(2n)
阶乘时间:O(n!)
O(nn)
一般代码的时间复杂度为指数阶及以上,就不用考虑了,哪怕 n 只有 10000,结果也是天大的数字,除非你确定 n 十分的小,将来也不会增加。
计算 1 到 n 的数之和,来看看哪种算法时间效率高:
普通人想到的是一个个累加,用代码描述:
int n = 100;// 1
int sum = 0;// 1
for (int i = 1; i <= n; i++) {// n + 1
sum += i;// n
}
System.out.println(sum);// 1
记录所有语句执行次数:2n + 4,时间复杂度:O(n);
前 n 次顺利通过 for 循环的判断条件,第 n + 1 次时判断失败,没有进入。
高斯想到的是首尾相加 * 个数 / 2:
int n = 100;// 1
int sum = (1 + n) * n / 2;// 1
System.out.println(sum);// 1
时间复杂度:O(1);
很明显高斯给出的算法效率更高;那么如果在某个程序中,需要解决求和问题,就可以选择此算法;而不是等到程序写好了,才掐着秒表,运行一下,一个个比哪个算法用的时间少。
我们可以看到,执行的代码就算有再多行,但如果与 n 的取值无关,通通记为 O(1),所以我只计算循环内某段语句的执行次数(受 n 影响),如 sum += i,其外的忽略不计,这样方便点。
算法优劣、数据的不同、数据量决定了程序的运行时间长短。
当数据量很少时,如 n = 2,计算机运行速度很快的,时间差异几乎是 0;使用事后计时的方法,是无法准确区分算法优劣的。
备注,高斯思路描述如下:
sum = 1 + 2 + ... + 100 sum = 100 + 99 + ... + 12sum = 101 + 101 + ... + 101 = 101 * 100
sum = 2sum / 2 = 101 * 50 = 5050
6.3.2 空间复杂度
代码耗费的存储空间,记作 S(n),同样也有 S(n) = O( f(n) ),O( f(n) ) 记为空间复杂度。
要求:记录一张 n * n 棋盘上的黑白棋子。
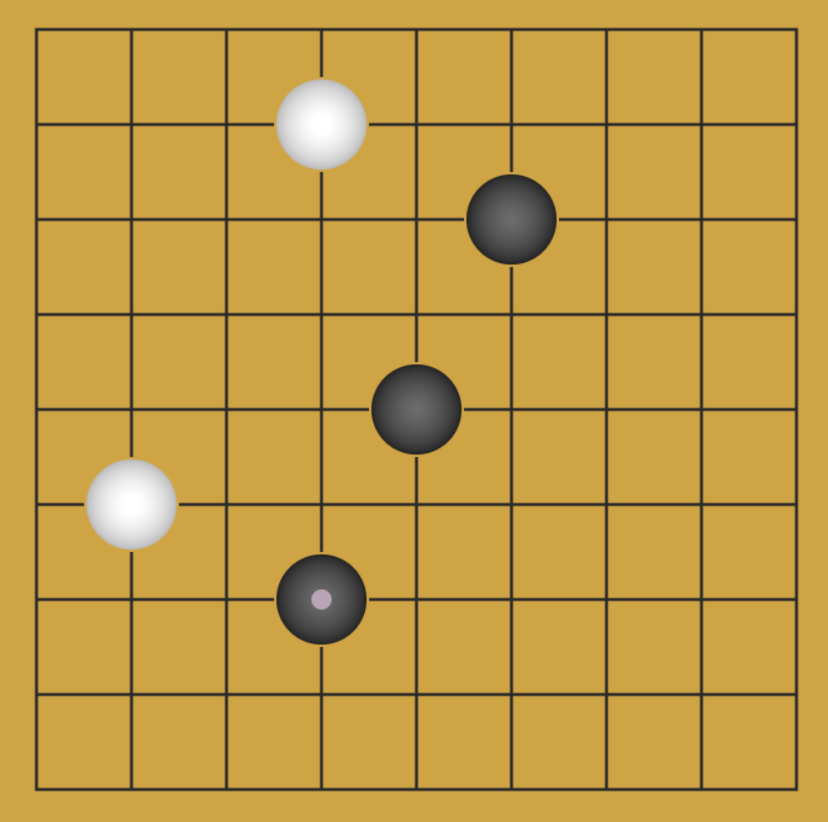
代码 1:使用二维数组记录棋盘,空记为 0,黑记为 1,白记为 2;假设 n = 9:
int[][] arr = {
{0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 2, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0, 0},
{0, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0},
};
数组所占空间:一个 int 类型是 4 个字节,S(n) = 4 * n2,空间复杂度为 O(n2);
想要获取第 row 行、第 column 列的信息:
public static void getState(int[][] arr, int row, int column) {
// 注意下标从 0 开始,并不是 1,所以需要减去 1
// 例:第 1 行第 1 列,即 arr[0][0]
int data = arr[row - 1][column - 1];
System.out.println("第 " + row + " 行、第 " + column + " 列的棋子为:" + printChess(data));
}
public static String printChess(int data) {
String state = "?";
switch(data) {
case 0 :
state = "空";
break;
case 1 :
state = "黑";
break;
case 2 :
state = "白";
break;
default:
}
return state;
}
时间复杂度为 O(1)。
代码 2:创建二维数组保存数据
第一行记录数组一共 i 行 j 列,有 count 个棋子(目前是 9、9、5);剩下 count 行记录这些棋子的位置(下标从 0 开始)与保存的值;数组长度为 1 + count。
int[][] arr = {
{9, 9, 5},// 棋盘的总行、列数、棋子的个数
{1, 3, 2},// 第一个棋子的行数 - 1、列数 - 1、保存的值
{2, 5, 1},
{4, 4, 1},
{5, 1, 2},
{6, 3, 1}
};
count 的范围处于 [0, n2] 之间;
如果棋盘上没有一个棋子,最好情况;只记录棋盘几行几列、棋子的个数为 0,数组所占空间:S(n) = 4 * 3 = 12,空间复杂度为 O(1);
如果棋盘上放满了棋子,最差情况;需要记录 n2 个棋子的位置,数组所占空间:S(n) = 4 * 3 * (n2 + 1) = 12n2 + 12,空间复杂度为 O(n2)。
获取第 row 行、第 column 列的信息,比如获取第 3 行第 6 列的信息,如果棋子存在,那么二维数组中肯定记录了 2、5、棋子保存的值。
我们需要从头遍历,找到开头为 2、5 的一维数组;如果找到,说明棋子存在,获取这个一维数组第 3 个元素(保存的值);
如果没有找到,棋子不存在,记为空。
public static void getState(int[][] arr, int row, int column) {
int i = row - 1;
int j = column - 1;
int data = 0;
for(int m = 1; m < arr.length; m++) {
if (arr[m][0] == i && arr[m][1] == j) {
data = arr[m][2];
break;
}
}
System.out.println("第 " + row + " 行、第 " + column + " 列的棋子为:" + printChess(data));
}
这种方式时间复杂度十分不稳定,最好情况 count = 0,不需要遍历,得到结果为空,时间复杂度为 O(1);最差情况 count = n2,且对应一维数组在最后一个,时间复杂度为 O(n2)。
当棋子较少时,使用代码 2 更节省空间;想要获取某行某列的信息,使用代码 1 时间效率更高。到底是用空间换时间,还是用时间换空间,凭自己取舍。
也可以组合:当用户下棋时,为了提升时间效率,用空间换时间,使用代码 1;退出棋盘时并不需要获取某行某列的信息,只需记录棋盘位置,使用代码 2 更节省空间。
6.3.3 冒泡排序
规定从小到大排序,那么小的要在前面,否则就需要交换。
Bubble Sort 算法思路:比较相邻元素,逆序就交换。
以 5,6,74,2,36,7 为例,每次比较中,我会用灰色标记大数。
第一轮:5,6,74,2,36,7
首先比较第 1 个与第 2 个元素的大小,5 < 6,不需要交换;
比较第 2 个与第 3 个,6 < 74,不需要交换;
比较第 3 个与第 4 个,74 > 2,需要交换,交换后:5,6,2,74,36,7
比较第 4 个与第 5 个,74 > 36,需要交换,交换后:5,6,2,36,74,7
比较第 5 个与第 6 个,74 > 7,需要交换,交换后:5,6,2,36,7,74

可以看到第一轮只是把最大的数归位了,继续找出第二大数吧。
第二轮:5,6,2,36,7,74
比较第 1 个与第 2 个,5 < 6,不需要交换;
比较第 2 个与第 3 个,6 > 2,需要交换,交换后:5,2,6,36,7,74
比较第 3 个与第 4 个,6 < 36,不需要交换;
比较第 4 个与第 5 个,36 > 7,需要交换,交换后:5,2,6,7,36,74

这一轮找出了第二大数 36。
有人这时可能会问,需不需要比较第 5 个与第 6 个?
要知道我们第一轮排序时,已经把最大的数放在了最后面,其它的数肯定不会大于最大数,所以没有必要进行比较了,剩下几轮同理,如下一轮只需比较到第 3 个与第 4 个,找出第三大数。
第三轮:5,2,6,7,36,74
比较第 1 个与第 2 个,5 > 2,需要交换,交换后:2,5,6,7,36,74
比较第 2 个与第 3 个,5 < 6,不需要交换;
比较第 3 个与第 4 个,6 < 7,不需要交换;
第三轮找出了第三大数 7。

第四轮:2,5,6,7,36,74
比较第 1 个与第 2 个,2 < 5,不需要交换;
比较第 2 个与第 3 个,5 < 6,不需要交换;
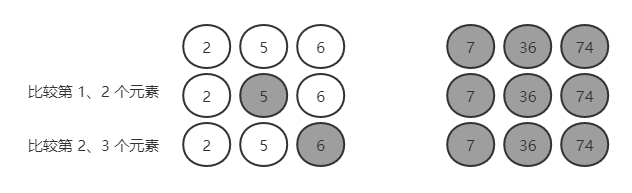
找出了第四大数 6。
第五轮:2,5,6,7,36,74
比较第 1 个与第 2 个,2 < 5,不需要交换;
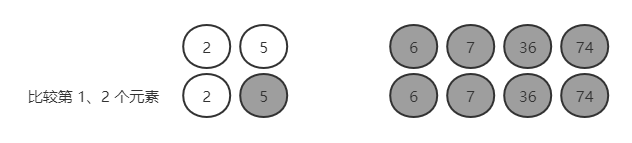
找出了第五大数 5,接下来就只剩 2,没必要比了,到此结束。可以看出一个长度为 6 的数组,需要 5 轮才能排好序,轮数正是数组长度 - 1。
使用代码实现:
之前在整数类型中讲过两数如何交换值,这里借助第三个变量 temp。
注意下标从 0 开始,如第一轮,arr[0] 与 arr[1] 比较、arr[1] 与 arr[2] 比较、...、arr[4] 与 arr[5] 比较,一共 5 次,那么定义一个变量从 0 到 4 即可。
int[] arr = {5, 6, 74, 2, 36, 7};
int temp = 0;
// 第一轮
for (int j = 0; j < 5; j++) {
// 如果逆序就交换
if (arr[j] > arr[j + 1]) {// 比较 5 次
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
// 第二轮
for (int j = 0; j < 4; j++) {
if (arr[j] > arr[j + 1]) {// 比较 4 次
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
// 第三轮
for (int j = 0; j < 3; j++) {
if (arr[j] > arr[j + 1]) {// 比较 3 次
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
// 第四轮
for (int j = 0; j < 2; j++) {
if (arr[j] > arr[j + 1]) {// 比较 2 次
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
// 第五轮
for (int j = 0; j < 1; j++) {
if (arr[j] > arr[j + 1]) {// 比较 1 次,即 arr[0] 与 arr[1]
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
// 遍历arr
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ",");
}
可是你发现了,每轮对应的 for 循环都几乎一模一样,只是判断条件从 j < 5,j < 4 ...到 j < 1,可以考虑使用外层循环将其包裹,定义一个 i 从 5 到 1,让 j < i,而这个 5 正是数组的长度 - 1。
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
改进:
可以发现第三轮时就已经排好序了,再也没有交换元素,剩下几轮都是无用功。可以定义一个 boolean 变量,默认为 true。
每次循环开始赋值 false;如果交换了,说明有逆序,需要继续循环,改为 true;如果没有交换,证明已经排好序了,需要退出循环。
boolean flag = true;
// flag 为 false 时,退出循环
for (int i = arr.length - 1; i > 0 && flag; i--) {
flag = false;
for (int j = 0; j < i; j++) {
// 逆序就交换
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
// 还要继续循环
flag = true;
}
}
}
改进后,设参与排序的数组长度为 n;
分析排序算法时,传统方式是衡量元素之间的比较和交换的次数。
最坏情况:数组为逆序,每次比较都需要交换,比较次数为:\(\sum\limits_{i=1}^{n-1}i\) = 1 + 2 + ... + (n - 1) = n * (n - 1) / 2,时间复杂度为 O(n2);
最好情况:数组为顺序,当 i = n - 1 时,进入外循环,里循环 j 从 0 到 n - 2,一共 n - 1 次比较,没有进入 if 语句内,flag = false,下一次外循环直接退出。时间复杂度为 O(n)。
空间复杂度为 O(1)。(与 n 无关,统统记为 O(1))
输入的数据如数组 arr,只取决于问题本身,与算法无关,不计入空间复杂度,只需计入算法实现所用的辅助空间,如 temp。
包括输出数组的内容(查看数组是否已经排序好了),都不计入。
6.3.4 简单选择排序
Simple Selection Sort 算法思路:找出小数,放在前面;第 i 轮找出第 i 小数,放在第 i 个位置。
小数:两数比较中,更小的数,我说的并不是 1.241 这种小数。
以 {5,2,6,252,1} 为例;小数使用灰色标记。
第一轮:5,2,6,252,1
比较第 1 个与第 2 个元素大小,5 > 2,小数为第 2 个;
比较第 2 个与第 3 个,2 < 6,小数为第 2 个;
比较第 2 个与第 4 个,2 < 252,小数为第 2 个;
比较第 2 个与第 5 个,2 > 1,小数为第 5 个;结束。
最小数在第 5 个位置上,应该放在第 1 个位置上。
交换第 5 个与第 1 个元素位置后:1,2,6,252,5
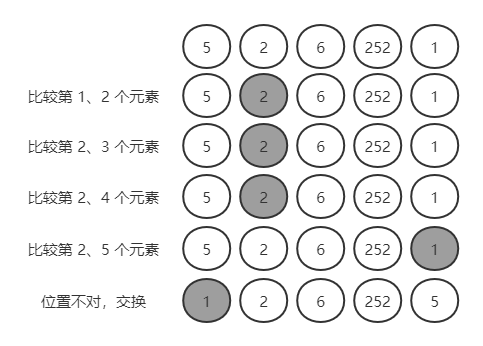
第一轮,找出了最小数并放在了合适的位置,那么接着找第二小数。
第二轮:1,2,6,252,5
比较第 2 个与第 3 个,2 < 6,小数为第 2 个;
比较第 2 个与第 4 个,2 < 252,小数为第 2 个;
比较第 2 个与第 5 个,2 < 5,小数为第 2 个;结束。
第二小数在第 2 个位置上,正好合适,不需要交换:1,2,6,252,5

不需要比较第 1 个与第 2 个,因为第 1 个是最小数,但我们找的是第二小数,下面同理。
第三轮:1,2,6,252,5
比较第 3 个与第 4 个,6 < 252,小数为第 3 个;
比较第 3 个与第 5 个,6 > 5,小数为第 5 个;结束。
第三小数在第 5 个位置上,应该放在第 3 个位置上。
交换第 5 个与第 3 个元素位置:1,2,5,252,6
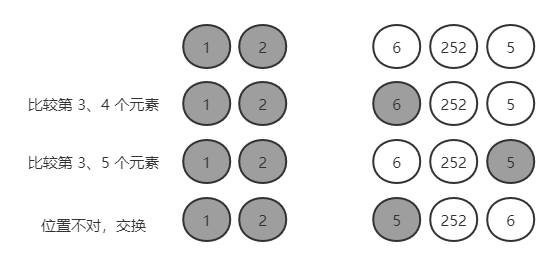
第四轮:1,2,5,252,6
比较第 4 个与第 5 个,252 > 6,小数为第 5 个;结束。
第四小数在第 5 个位置上,应该放在第 4 个位置上。
交换第 5 个与第 4 个元素位置:1,2,5,6,252
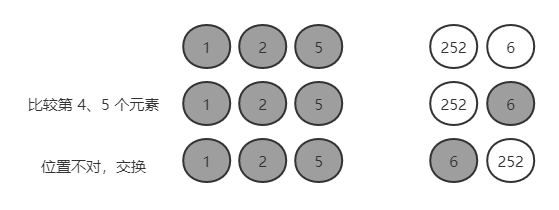
5 个数,已经确定了 4 位,剩下一个数自动归位;轮数为数组长度 - 1。
使用代码实现:
我们可以看到每轮都是拿小数与其它数进行比较,所以需要定义变量如 min,记录小数的下标;设数组长度为 n。
如第 1 轮假设最小数下标也就是 min 为 0,然后让 arr[min] 与剩下的数,即与下标为 1、2、3 ... n - 1 的元素比较;期间,若发现更小数,将 min 替换为此数的下标,然后拿 arr[min] 继续与其它数比较。
第 2 轮设 min 为 1;
第 3 轮设 min 为 2;
...
第 n - 1 轮设 min 为 n - 2。
int[] arr = {5, 2, 6, 252, 1};
int n = arr.length;// n = 5
int temp = 0;
// 第一轮:找最小数,假设最小数下标为 0
int min = 0;
// 下标为 0 的数,与下标为 1、2、3、4 的元素进行比较
for (int j = 1; j < n; j++) {
// 比较过程中,发现有更小的,将 min 替换为此数下标,保证 min 一直记录的是最小数的下标
if (arr[j] < arr[min]) {// 比较 4 次
min = j;
}
}
// 如果 min 不等于 0,证明最小数的下标不是 0,需要将最小数与下标为 0 的元素交换位置
if (min != 0) {
temp = arr[0];
arr[0] = arr[min];
arr[min] = temp;
}
// 第二轮:找出第二小数,假设第二小数下标为 1(因为下标为 0 的元素已经被确定为最小数,无需参与比较)
min = 1;
// 下标为 1 的数,与下标为 2、3、4 的元素进行比较
for (int j = 2; j < n; j++) {
if (arr[j] < arr[min]) {// 比较 3 次
min = j;
}
}
if (min != 1) {
temp = arr[1];
arr[1] = arr[min];
arr[min] = temp;
}
// 第三轮
min = 2;
for (int j = 3; j < n; j++) {
if (arr[j] < arr[min]) {// 比较 2 次
min = j;
}
}
if (min != 2) {
temp = arr[2];
arr[2] = arr[min];
arr[min] = temp;
}
// 第四轮
min = 3;
for (int j = 4; j < n; j++) {
if (arr[j] < arr[min]) {// 比较 1 次
min = j;
}
}
if (min != 3) {
temp = arr[3];
arr[3] = arr[min];
arr[min] = temp;
}
// 利用 Arrays 类的 toString 方法输出 arr 的内容
System.out.println(Arrays.toString(arr));
每轮对应的 for 循环几乎一致,观察每轮的变化之处:min = 0、1、2 ... n - 2,j = 1、2、3 ... n - 1。
考虑外层 for,定义 i 从 0 到 n - 2,让 min = i,j = i + 1。
for (int i = 0; i < n - 1; i++) {
int min = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
if (min != i) {
temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
}
简单选择排序,比较时没有交换元素,分开讨论:
比较次数是固定的,一共为 1 + 2 + ... + (n - 1) = n * (n - 1) / 2。
交换次数,最好情况不用交换,次数为 0;最坏情况,每次位置都不对,需要交换,次数为 n - 1。
综合,时间复杂度为 O(n2),空间复杂度为 O(1)。
6.3.5 直接插入排序
Insert Sort 算法思路:新元素与前面已排序的元素进行比较,并将它插入到正确的位置。
以 {25, 6, 50, 26} 一共四个元素为例,灰色元素的集合代表有序序列,当所有元素都为灰色时代表已经排好序了。
第一轮:25,6,50,26
arr[1] 与 arr[0] 比较,6 < 25,逆序,需要交换,交换后:6,25,50,26
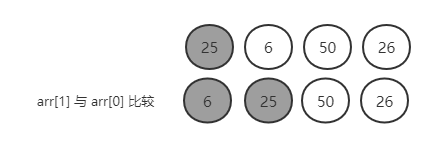
那么前面两个元素已经排好序了。
第二轮:6,25,50,26
arr[2] 与 arr[1] 比较,50 > 25,顺序,不需要交换
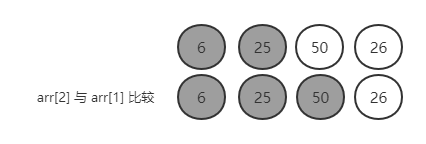
arr[2] 不需要跟 arr[0] 比较,因为通过第一轮排序,确定了 arr[1] > arr[0],如果 arr[2] > arr[1],必然有 arr[2] > arr[0],大小已经确定,无需比较,下面同理。(如果后面的元素大于前面,不需要交换,说明顺序是对的,无需比较,直接终止操作)
前面三个元素排好序了。
第三轮:6,25,50,26
arr[3] 与 arr[2] 比较,26 < 50,交换后:6,25,26,50
arr[2] 与 arr[1] 比较,26 > 25,不需要交换
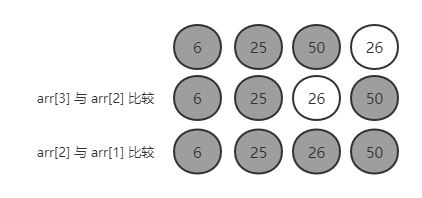
前面四个元素排好序了;到此为止,一共 arr.length - 1 轮。
代码描述:
只有后面元素小于前面元素才需要交换,否则就终止循环;在循环期间,需要保证后面元素下标大于 0(避免下标越界)。
int[] arr = {25, 46, 3, 8};
int temp = 0;
// 第一轮
for (int j = 1; j > 0 && arr[j] < arr[j - 1]; j--) {
temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
}
// 第二轮,最差情况比较 2 次。
for (int j = 2; j > 0 && arr[j] < arr[j - 1]; j--) {
temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
}
// 第三轮
/*
最差情况,比较 3 次;即 arr[3]、arr[2] 比较,arr[2]、arr[1] 比较,
arr[1]、arr[0] 比较。
*/
for (int j = 3; j > 0 && arr[j] < arr[j - 1]; j--) {
temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
}
j 从 1 到 arr.length - 1,考虑定义外层 for 循环,i 从 1 到 arr.length - 1;让 j = i。
结合:
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
}
}
最差情况:参与排序的数组为逆序,每次的新元素都比前面所有的元素小,需要移动到数组最前面,设数组长度为 n,一共 n - 1 轮排序,比较次数为 1 + 2 + ... + (n - 1) = \(\frac{n(n-1)}{2}\);时间复杂度为 O(n2)。
最好情况:参与排序的数组为顺序,每次新元素都大于前面的元素,刚进入 for 循环,比较结果为 false,直接退出循环;一共 n - 1 比较,时间复杂度为 O(n)。
空间复杂度为 O(1)。
变体:
将新元素与前面的元素比较,获取新元素应该插入的位置,并把已有元素往后移,给新元素腾出一个空间。
以 {6,3,5,7,1} 为例:
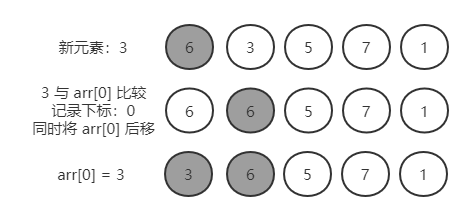
第一轮:6,3,5,7,1
记录新元素的值:insertVal = arr[1] = 3
insertVal 与 arr[0] 比较,3 < 6,记录新元素应该插入的位置:insertIndex = 0
将 arr[0] 后移腾出空间:6,6,5,7,1
结束
根据记录的下标插入新元素:arr[insertIndex] = arr[0] = insertVal = 3
插入后:3,6,5,7,1
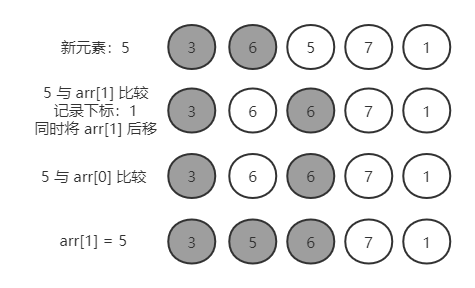
第二轮:3,6,5,7,1
记录 insertVal = arr[2] = 5
insertVal 与 arr[1] 比较,5 < 6,记录下标 1,将 arr[1] 后移:3,6,6,7,1
insertVal 与 arr[0] 比较,5 > 3,结束
插入新元素,arr[1] = insertVal = 5
3,5,6,7,1
第三轮:3,5,6,7,1
记录 insertVal = arr[3] = 7
insertVal 与 arr[2] 比较,7 > 6,结束

第四轮:3,5,6,7,1
记录 insertVal = arr[4] = 1
insertVal 与 arr[3] 比较,1 < 7,记录下标 3,将 arr[3] 往后移:3,5,6,7,7
insertVal 与 arr[2] 比较,1 < 6,记录下标 2,将 arr[2] 往后移:3,5,6,6,7
insertVal 与 arr[1] 比较,1 < 5,记录下标 1,将 arr[1] 往后移:3,5,5,6,7
insertVal 与 arr[0] 比较,1 < 3,记录下标 0,将 arr[0] 往后移:3,3,5,6,7
结束
arr[0] = insertVal = 1
1,3,5,6,7

int[] arr = {6, 3, 5, 7, 1};
for (int i = 1; i < arr.length; i++) {
// 记录下标
int insertIndex = i;
// 新元素的值
int insertVal = arr[i];
// 拿新元素与之前的元素比较
for (int j = i; j > 0 && insertVal < arr[j - 1]; j--) {
// 记录新元素应该插入的下标
insertIndex = j - 1;
// 将 arr[j - 1] 后移,即让 arr[j] 保存 arr[j - 1] 的值
arr[j] = arr[j - 1];
}
if (i != insertIndex) {
arr[insertIndex] = insertVal;
}
}
代码的第 16 行说明:insertIndex 默认为 i(新元素的下标),经过循环后 insertIndex 如果还是 i,说明新元素的位置正合适,不用变动。
这种实现比第一种方式,由于交换次数的减少,稍微快一点点。
标签:arr,1.1,temp,min,int,复杂度,6.3,排序,比较 来源: https://www.cnblogs.com/cqhh/p/16147485.html