[AGC032E] Modulo Pairing

题面

用的都是AT官方题解的图。

观察样例

3 10
0 2 3 4 5 9

样例解释给出的配对方式是 \((0,5)\)，\((2,3)\)，\((4,9)\)，

也存在一种方案是：\((0,4)\)，\((2,3)\)，\((5,9)\)

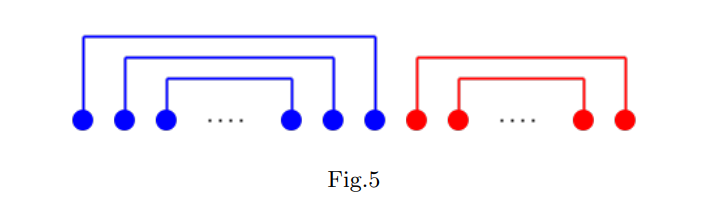
我们猜测：对 \(a\) 进行排序后，存在一种最优解的方案：分成了两个区间，蓝线表示 \(x+y<m\)，红线表示 \(x+y\ge m\)，蓝线区间内首尾配对，红线区间内首尾配对。

Proof
我们考虑证明任意方案，都能转化为一种这种形式的方案，且答案不劣于转化前的方案。

就不逐个证明了，证明一下右上角的。
已知 \(a<b<c<d,a+c<m,b+d\ge m\)，证明 \(a+b<m,c+d\ge m,max\{(a+c)\bmod m,(b+d)\bmod m\}\ge max\{(a+b) \bmod m,(c+d)\bmod m\}\)

\[a+b<m,c+d\ge m \text{ 显然}\\ (a+b)\bmod m=a+b\le a+c=(a+c)\bmod m\\ (c+d)\bmod m=c+d-m\le c+a=(a+c)\bmod m\\ max\{(a+b) \bmod m,(c+d)\bmod m\}\le (a+c)\bmod m \le max\{(a+c)\bmod m,(b+d)\bmod m\} \]

那么我们现在考虑枚举红蓝边界，并判断合法性，更新答案，这是 \(O(n^2)\) 的，会TLE。

实际上是可以二分边界的。因为满足下列三个条件，所以我们只要在合法的情况下尽量把边界左移即可。

• 越往左，左边的越容易满足蓝色条件。因此左移时不用考虑左边。
• 越往左，右边的越不容易满足红色条件，所以到左移到某一点如果右边不满足了，再往左移，就更不可能满足了。
• 最重要的：越往左移，答案越优。比较显然。

标签：方案,左移,Modulo,边界,Pairing,样例,满足,AGC032E,越往
来源： https://www.cnblogs.com/zdsrs060330/p/16063629.html