CSAPP lab1 datalab
作者:互联网
#bitXor
用位运算模拟异或运算,这里用到了摩根定律:
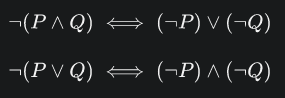
int bitXor(int x, int y) {
// x^y = (~x&y) | (x~&y) = ~(~(~x&y) & ~(x&~y))
return ~(~(~x & y) & ~(x & ~y));
}
#tmin
有符号整型数表示的最小数的位模式中,最高位是1,其余位全为0
int tmin(void) {
return 1 << 31;
}
#isTmax
可以发现最大数的位模式除了最高位是0,其余位全为1。对其加1后再取反,会重新得到最大数(注意-1也满足,需要特判)。由于不能用==,用^运算替代(a^a=0)
int isTmax(int x) {
// 注意特判-1
return !(~(x + 1) ^ x) & !!(x + 1);
}
#allOddBits
本题的要求是判断一个整型数字的奇数位是否全为1。主要是构建一个奇数位全为1,偶数位全为0的掩码(0xAAAAAAAA)。
int allOddBits(int x) {
int a = 0xAA << 8;
int b = a | 0xAA;
int c = (b << 16) | b;
return !((x & c) ^ c);
}
#negate
基本性质:对一个整数位取反,然后加1,就可以得到相反数。
int negate(int x) {
return ~x + 1;
}
#isAsciiDigit
本题的要求是判断x是否在区间0x30~0x39中。先判断x的高32位是否等于3,再判断x的低4位是不是在0x0~0x9中,对于低4位的判断,可以让低4位减掉0xa,判断结果是否<0。
int isAsciiDigit(int x) {
int a = x >> 4;
int b = ~0xA + 1;
int c = (x & 0xF) + b;
return (!(a ^ 0x3)) & (c >> 31 & 0x1);
}
#conditional
本题的关键是构建出一个掩码,实现类似于(mask&y)|(~mask&z)的形式,考虑0的补码为全0,-1的补码为全1。
int conditional(int x, int y, int z) {
// a = x ? 1 : 0
int a = !!x;
int b = ~a + 1;
return (b & y) | (~b & z);
}
#isLessOrEqual
要实现判断y>=x,即判断y-x的符号位。可以分情况讨论:当x与y同号时,应该满足y-x>=0。当x与异号时,应该满足y>=0,x<0
int isLessOrEqual(int x, int y) {
int sign_x = x >> 31 & 0x1, sign_y = y >> 31 & 0x1;
// c = y - x
int c = y + (~x + 1), sign_c = c >> 31 & 0x1;
// 分两种情况讨论,当x,y异号时,需满足y>=0,x<0
// 当x,y同号时,应满足c>=0
int flag = sign_x ^ sign_y;
return (flag & sign_x & ~sign_y) | (!flag & !sign_c);
}
#logicalNeg
实现!运算。受到conditional的启发,-1的补码为全1,0的补码为全0。由于除了0以外所有的整数与它的相反数做|运算后,符号位一定为1,可以将x与其相反数做|运算后,右移31位,这样当x为0时,移位后就可以得到0(全0),当x非0时,移位后就可以得到-1(全1),最后再+1即可。
int logicalNeg(int x) {
return ((x | (~x + 1)) >> 31) + 1;
}
#howManyBits
这题目的意思是给一个数字x,问最少能用多少位的补码数来表示。对于正数,就是找最高位为1的位数,之后再加1(符号位)。对于负数,找最高位为0的位数,再加1。找最高位的1出现在哪一位时,用到了二分查找,代码如下:
int howManyBits(int x) {
//
int b0, b1, b2, b4, b8, b16;
int sign;
sign = x >> 31;
// 若x是负数,则对x取反以便统一处理。否则保持不变
// 找到x中最高位为1的位数,最后加1(符号位)即为答案
x = (~sign & x) | (sign & ~x);
// x的高16位是否有1
b16 = !!(x >> 16) << 4;
x = x >> b16;
b8 = !!(x >> 8) << 3;
x = x >> b8;
b4 = !!(x >> 4) << 2;
x = x >> b4;
b2 = !!(x >> 2) << 1;
x = x >> b2;
b1 = !!(x >> 1);
x = x >> b1;
b0 = !!x;
return b0 + b1 + b2 + b4 + b8 + b16 + 1;
}
接下来这部分是浮点数相关操作,回顾一下浮点数的表示方法,可以参考这个链接:CSAPP浮点数笔记。
下图是单精度浮点数的表示方法:
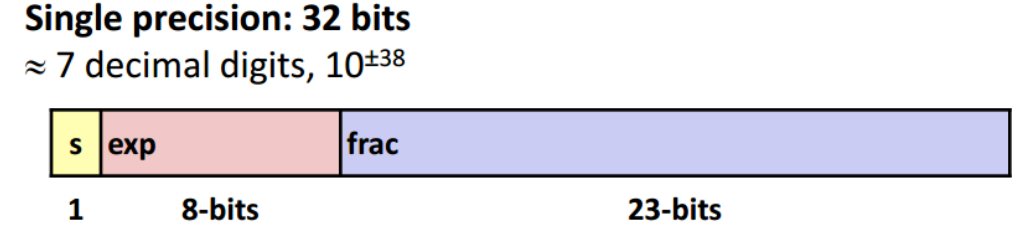
最高位是符号位,中间8位是阶码,末尾32位是尾数。
\(V=(-1)^s\times2^E\times M\),s是符号位,E是阶码,M是尾数。注意区分该公式中的E和图中的exp。
当exp不为全1且不为全0时,表示的值为规格化值。阶码字段代表无符号数e,那么公式中的E=exp-Bias。Bias是偏置值,值为\(2^k-1\),其中k为阶码字段的位数。对于单精度浮点数,Bias=127。
规划化值的frac字段还有隐含的1,即M=1+frac。
当exp为全0时,表示的值为非规格化值。此时E=1-Bias,并且frac字段不含隐含的1,即M=frac
当exp为全1,frac为全0时,表示的值为无穷大,s=1时表示负无穷,s=0时表示正无穷。当exp为全1,但frac不为全0时,表示NaN(Not a Number)。
#floatScale2
本题的要求是返回2*x的浮点位表示。先通过位运算把单精度浮点数的各字段取出。当exp为全1时,uf为NaN或者无穷大,此时直接返回uf。当exp为全0时,uf是非规格化数,此时需要把尾数frac左移1位。一般情况下,让阶码exp左移1位即可。
unsigned floatScale2(unsigned uf) {
int sign, exp, frac;
sign = uf >> 31 & 0x1, exp = (uf & 0x7f800000) >> 23, frac = uf & 0x7fffff;
// 当uf表示NaN或者无穷大时
if (exp == 0xff)
return uf;
// 当uf为非规格划数时
if (exp == 0)
return (sign << 31) | (exp << 23) | (frac << 1);
// 一般情况
return (sign << 31) | ((exp + 1) << 23) | frac;
}
#floatFloat2Int
本题要实现浮点数--》整型数的强制转换。首先让exp减掉偏置值得到真实的阶码值,当e<0时,表示的是小数0.xxxxx,转化为整型数0。当e>=32-1(符号位)时,说明该浮点数已经比最大整型数大,返回0x80000000u,当0<=e<23时,要舍弃frac字段的后23-e位,当23<=e<31时,frac还需要左移e-23位。
int floatFloat2Int(unsigned uf) {
int sign, exp, frac, e;
sign = uf >> 31 & 0x1, exp = (uf & 0x7f800000) >> 23, frac = uf & 0x7fffff;
e = exp - 127;
if (e < 0)
return 0;
if (e >= 31)
return 0x80000000u;
frac = (1 << 23) | frac;
if (e < 23)
frac = frac >> (23 - e);
else
frac = frac << (e - 23);
if (sign)
frac = -frac;
return frac;
}
#floatPower2
该函数是要返回2^x的浮点位模式。当x>127时候,说明2^x已经>=无穷大(无穷大的阶码是全1(255),减掉偏置值(127)也就是128)。当x<-126时,说明2^x已经非常小了(当exp为全0时,此时偏置值为1-127=-126,这是除去无穷小外最小的浮点数),应返回0。对于一般情况(可规格化数), 直接让阶码部分等于x+127。
unsigned floatPower2(int x) {
// 无穷大
if (x > 127)
return 0x7f800000u;
// 比最小值还要小
if (x < -126)
return 0;
// 一般情况
return (x + 127) << 23;
}
标签:datalab,return,int,CSAPP,sign,lab1,exp,frac,uf 来源: https://www.cnblogs.com/Kyo-Kyo/p/16031468.html