Leetcode 277.搜索名人（中等） 图相关-名流问题

277. 搜索名人（中等）

题目：

给你 n 个人的社交关系（你知道任意两个人之间是否认识），然后请你找出这些人中的「名人」。

所谓「名人」有两个条件：

1、所有其他人都认识「名人」。

2、「名人」不认识任何其他人。

在本题中，你可以使用辅助函数 bool knows(a, b) 获取到 A 是否认识 B。请你来实现一个函数 int findCelebrity(n)。

派对最多只会有一个 “名人” 参加。若 “名人” 存在，请返回他/她的编号；若 “名人” 不存在，请返回 -1。

这是一个图相关的算法问题，社交关系嘛，本质上就可以抽象成一幅图。

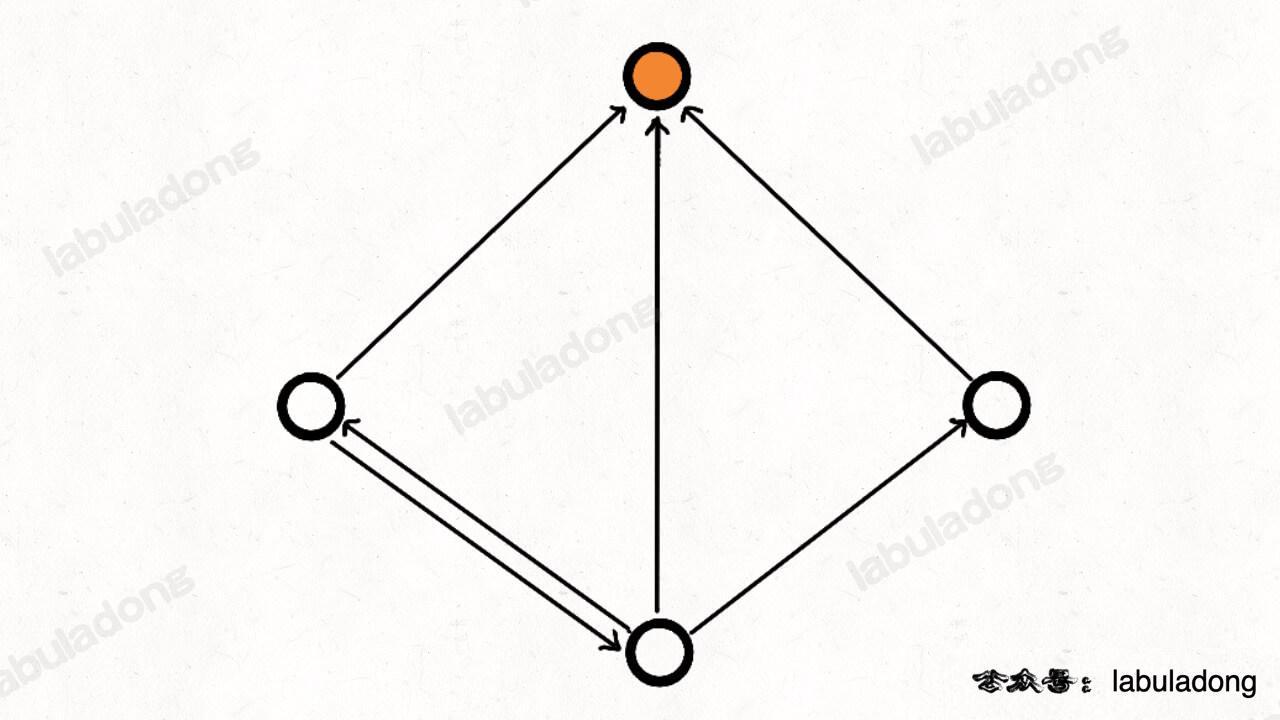
如果把每个人看做图中的节点，「认识」这种关系看做是节点之间的有向边，那么名人就是这幅图中一个特殊的节点：

这个节点没有一条指向其他节点的有向边；且其他所有节点都有一条指向这个节点的有向边。

或者说的专业一点，名人节点的出度为 0，入度为 n - 1。

思路：

labuladong

因为「名人」的定义保证了「名人」的唯一性，所以我们可以利用排除法，先排除那些显然不是「名人」的人，从而避免 for 循环的嵌套，降低时间复杂度。

只要观察任意两个候选人的关系，我一定能确定其中的一个人不是名人，把他排除。

至于另一个候选人是不是名人，只看两个人的关系肯定是不能确定的，但这不重要，重要的是排除掉一个必然不是名人的候选人，缩小了包围圈。

设这两个人的编号分别是 cand 和 other，然后我们逐一分析每种情况，看看怎么排除掉一个人。

对于情况一，cand 认识 other，所以 cand 肯定不是名人，排除。因为名人不可能认识别人。

对于情况二，other 认识 cand，所以 other 肯定不是名人，排除。

对于情况三，他俩互相认识，肯定都不是名人，可以随便排除一个。

对于情况四，他俩互不认识，肯定都不是名人，可以随便排除一个。因为名人应该被所有其他人认识。

综上，只要观察任意两个之间的关系，就至少能确定一个人不是名人，上述情况判断可以用如下代码表示：

题目给出了已实现API knows用来判断a是否认识b

class Solution {
public:
    int findCelebrity(int n) {
        queue<int> q;
        for(int i=0;i<n;++i){
            q.push(i);
        }
        while(q.size()>=2){
            int cand=q.front();
            q.pop();
            int other=q.front();
            q.pop();
            // other认识cand且cand不认识other，other肯定不是名人
            if(knows(other,cand)&&!knows(cand,other)){
                q.push(cand);
            }else{
                //cand肯定不是名人
                q.push(other);
            }
        }
        int cand=q.front();
        for(int i=0;i<n;++i){
            if(i==cand){
                continue;
            }
            if(knows(i,cand)&&!knows(cand,i)){
                continue;
            }
            return -1;
        }
        return cand;
    }

};

标签：cand,名流,int,节点,认识,other,277,Leetcode,名人
来源： https://www.cnblogs.com/zl1991/p/15926332.html