其他分享
首页 > 其他分享> > 数学建模中的层次分析法笔记

数学建模中的层次分析法笔记

作者：互联网

1、层次分析法：用于评价类模型，建立模型要确定评价目标、实现目标的方案、评价准则。

2、层次分析法具体实现步骤（辅以具体例子说明）：

（1）建立层次结构

解决评价类问题想到的问题：

我们评价的目标是什么？

答：为小明同学选择最佳的旅游景点。

我们为了达到这个目标有哪几种可选的方案？

答：三种，分别是去苏杭、去北戴河和去桂林。

评价的准则或者说指标是什么？（我们根据什么东西来评价好坏） 答：景色、花费、居住、饮食、交通

由此得到层次结构如下

（2）构造层次结构图的判断矩阵

判断矩阵是正负反矩阵，数据由专家经验得出，但实际在比赛中是通过查资料得出。对应的元素a_{ij}指相对于j，i的重要程度，a^{ij}=\frac{1}{a^{ji}},a^{ii}=1,a_{ij}>0。用1-9表示重要程度，如下表所示

标度含义
1同样重要性
3稍微重要
5明显重要
7强烈重要
9极端重要
2，4，6，8上述两相邻判断的中值
倒数

A和B相比如果标度为3那么B和A相比就是1/3

  (3)对判断矩阵进行一致性检验

这一步即检验构造的判断矩阵与一致矩阵是否有太大差别

方法一

a_{ij}=i的重要程度/j的重要程度，a_{jk}=j的重要程度/k的重要程度

a_{ik}=i的重要程度/k的重要程度=a_{ij}\times a_{jk}

方法二

判断矩阵各行各列成比例即为一致矩阵

方法三

（1）计算一致性指标CI=\frac{\lambda_{max} -n}{n-1}

  (2)   查找对应的平均随机一致性指标RI

n123456789101112131415
RI000.520.891.121.261.361.411.461.491.521.541.561.581.59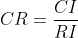
 （3）计算一致性比例 CR=\frac{CI}{RI}

程序实现

clear;clc;
A=[1 2 4;0.5 1 2;0.25 0.5 1];
[V,D]=eig(A);
[n,n]=size(A);
Max_eig=max(max(A));
CI=(Max_eig-n)/(n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  
CR=CI/RI(n);
disp('一致性比例CR=');disp(CR);
if(CR<0.1)
   disp('判断矩阵一致性可以接受');
else
   disp('判断矩阵一致性可以接受')
end

（4）由判断矩阵计算被比较元素对于该准则的相对权重

算术平均法

（1）将判断矩阵按照列归一化即每一个元素除以所在列的和

（2）将归一化各列相加

（3）将相加后得到的每项除n

clear;clc
A=[1 2 4;0.5 1 2;0.25 0.5 1];
Sum_A=sum(A);
[n,n]=size(A);
SUM_A=repmat(Sum_A,n,1);
Stand_A=A./SUM_A;
sum(Stand_A,2);
disp('算术平均法求权重的结果为：');
disp(sum(Stand_A,2)/n)
B=[1 1/3 1/8;3 1 1/3;8 3 1];
Sum_B=sum(B);
[n,n]=size(B);
SUM_B=repmat(Sum_B,n,1);
Stand_B=B./SUM_B;
sum(Stand_B,2);
disp('算术平均法求权重的结果为：');
disp(sum(Stand_B,2)/n)
C=[1 1 3;1 1 3;1/3 1/3 1];
Sum_C=sum(C);
[n,n]=size(C);
SUM_C=repmat(Sum_C,n,1);
Stand_C=C./SUM_C;
sum(Stand_C,2);
disp('算术平均法求权重的结果为：');
disp(sum(Stand_C,2)/n)
D=[1 1 1/4;1 1 1/4;4 4 1];
Sum_D=sum(D);
[n,n]=size(D);
SUM_D=repmat(Sum_D,n,1);
Stand_D=D./SUM_D;
sum(Stand_D,2);
disp('算术平均法求权重的结果为：');
disp(sum(Stand_D,2)/n)
E=[1 1/2 4 3 3;2 1 7 5 5;1/4 1/7 1 1/2 1/3;1/3 1/5 2 1 1 ;1/3 1/5 3 1 1];
Sum_E=sum(E);
[n,n]=size(E);
SUM_E=repmat(Sum_E,n,1);
Stand_E=E./SUM_E;
sum(Stand_E,2);
disp('算术平均法求权重的结果为：');
disp(sum(Stand_E,2)/n)

几何平均法

（1）将判断矩阵按行相乘得到新的列向量

（2）将新的向量每个分量开n次方

（3）对该向量进行均一化得到权重向量

clear;clc;
A=[1 2 4;0.5 1 2;0.25 0.5 1];
Product_A=prod(A,2);
[n,n]=size(A);
Product_n_A=Product_A.^(1/n);
disp('几何平均法求权重的结果为：');
disp(Product_n_A ./ sum(Product_n_A))
B=[1 1/3 1/8;3 1 1/3;8 3 1];
Product_B=prod(B,2);
[n,n]=size(B);
Product_n_B=Product_B.^(1/n);
disp('几何平均法求权重的结果为：');
disp(Product_n_B ./ sum(Product_n_B)) 
C=[1 1 3;1 1 3;1/3 1/3 1];
Product_C=prod(C,2);
[n,n]=size(C);
Product_n_C=Product_C.^(1/n);
disp('几何平均法求权重的结果为：');
disp(Product_n_C./ sum(Product_n_C))
D=[1 1 1/4;1 1 1/4;4 4 1];
Product_D=prod(D,2);
[n,n]=size(D);
Product_n_D=Product_D.^(1/n);
disp('几何平均法求权重的结果为：');
disp(Product_n_D./ sum(Product_n_D))
E=[1 1/2 4 3 3;2 1 7 5 5;1/4 1/7 1 1/2 1/3;1/3 1/5 2 1 1 ;1/3 1/5 3 1 1];
Product_E=prod(E,2);
[n,n]=size(E);
Product_n_E=Product_E.^(1/n);
disp('几何平均法求权重的结果为：');
disp(Product_n_E ./ sum(Product_n_E))

特征值法

（1）求最大特征值以及对应的特征向量，得最大特征值的位置

（2）对得出的特征向量进行归一化处理

clear;clc;
A=[1 2 4;0.5 1 2;0.25 0.5 1];
[V,D]=eig(A);
Max_eig=max(max(A));
D==Max_eig;
find(D,1);
[r,c]=find(D,1);
V(:,c);
disp('特征值法求权重的结果为：')
disp(V(:,c)./sum(V(:,c)))
B=[1 1/3 1/8;3 1 1/3;8 3 1];
[V,D]=eig(B);
Max_eig=max(max(B));
D==Max_eig;
find(D,1);
[r,c]=find(D,1)
V(:,c);
disp('特征值法求权重的结果为：')
disp(V(:,c)./sum(V(:,c)))
C=[1 1 3;1 1 3;1/3 1/3 1];
[V,D]=eig(C);
Max_eig=max(max(C));
D==Max_eig;
find(D,1);
[r,c]=find(D,1);
V(:,c);
disp('特征值法求权重的结果为：')
disp(V(:,c)./sum(V(:,c)))
D=[1 1 1/4;1 1 1/4;4 4 1];
[V,D]=eig(D);
Max_eig=max(max(D));
D==Max_eig;
find(D,1);
[r,c]=find(D,1);
V(:,c);
disp('特征值法求权重的结果为：')
disp(V(:,c)./sum(V(:,c)))
E=[1 1/2 4 3 3;2 1 7 5 5;1/4 1/7 1 1/2 1/3;1/3 1/5 2 1 1 ;1/3 1/5 3 1 1];
[V,D]=eig(E);
Max_eig=max(max(E));
D==Max_eig;

3、层次分析法的局限性

（1）决策层不能过多，n太大时判断矩阵和一致性矩阵差异可能会很大，一般n最大取15

（2）如果决策层中的数据是已知的

本笔记是根据清风老师的数学建模课第一节层次分析法总结出来的，感兴趣的小伙伴可以在B站上看哦~

标签：disp,Product,sum,建模,笔记,分析法,Stand,eig,法求
来源： https://blog.csdn.net/ffkkxx666/article/details/122514097