测评链接

题目大意：

若有序列 \(d_1,d_2...d_m\)，且 \(x_0=y_0=0\)，则对于任意 \(1 \leq i \leq m\) 可随意选择如下操作：

• 'U'：\((x_i,y_i)=(x_{i-1},y_{i-1}+d_i)\)
• 'D'：\((x_i,y_i)=(x_{i-1},y_{i-1}-d_i)\)
• 'L'：\((x_i,y_i)=(x_{i-1}-d_i,y_{i-1})\)
• 'R'：\((x_i,y_i)=(x_{i-1}+d_i,y_{i-1})\)

现给定 \(n\) 个坐标 \((X_1,Y_1),(X_2,Y_2)...(X_n,Y_n)\)，求一个序列使得对于 \(\forall 1 \leq i \leq n\) 均有一种操作方案使得 \((x_m,y_m)=(X_i,Y_i)\)，并求得每一个操作方案

\(1 \leq n \leq 1000,-10^9 \leq X_i,Y_i \leq 10^9\)

要求答案满足：\(1 \leq m \leq 40,1 \leq d_i \leq 10^{12}\)

解题过程：

排除一些常见算法后可以基本确定是一道构造题，由于随意取值首先考虑二进制

简单枚举前几个可以发现对于序列 \(1,2,4...2^k\) 可以经过操作后得到所有满足\(|x|+|y|\leq 2^{k+1}-1,|x|+|y| \equiv 1 \pmod2\) 的点 \((x,y)\)

用数学归纳法法证明：

1. \(k=0\) 时显然成立

2. 当 \(k\) 成立时，图中染色区域满足条件的点均可得到，被围白色区域待证
   

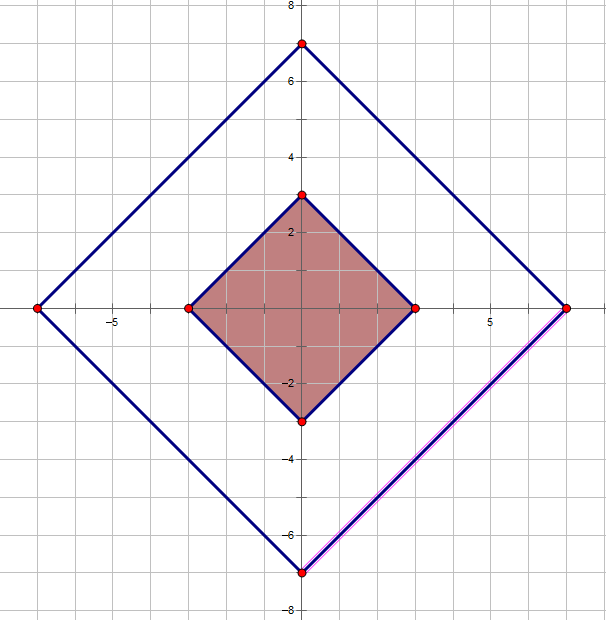
考虑到序列中多了 \(2^{k+1}\)，则任意满足条件的点都可以上下左右移动 \(2^{k+1}\) 格

即染色区域上下左右移动 \(2^{k+1}\) 格，如下图：

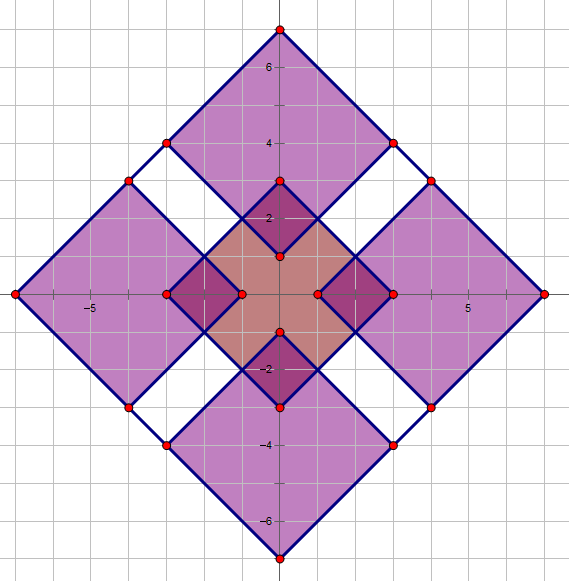
此时所有染色区域内符合条件的点均可得到

又简单计算可知原点与紫色区域相距 \(1\) 格，则白色区域内的点均不满足 \(|x|+|y| \equiv 1 \pmod 2\)

证毕

考虑实现过程：

由于 \(-10^9 \leq X_i,Y_i \leq 10^9\)，所以 \(m\) 最高只到三十几，不会超出范围

首先由于加减奇偶性一致，可根据 \(X_i+Y_i\) 的奇偶性判定无解

上面已证全是奇点对应的序列，如全是偶点，则在序列中加个 \(1\) 改为求奇点所对序列

考虑方案求法，对于任意一个奇点 \((X_i,Y_i)\)，若存在于 \(1\rightarrow 2^{k}\) 的序列所围住的正方形中

则根据以上证明，将 \(X_i,Y_i\) 中绝对值较大的往反方向走 \(2^k\) 格可得 \(1\rightarrow 2^{k-1}\) 的序列所对应的正方形中对应的奇点

以此类推，最终会推至点 \((0,0)\)，此时倒着走一遍就是方案

PS：走的时候注意正负和方向的改变

上代码：

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<iomanip>
#include<cstring>
#include<algorithm>
#include<ctime>
using namespace std;
inline int read()
{
	int kkk=0,x=1;
	char c=getchar();
	while((c<'0' || c>'9') && c!='-')
		c=getchar();
	if(c=='-')
		c=getchar(),x=-1;
	while(c>='0' && c<='9')
		kkk=(kkk<<3)+(kkk<<1)+(c-'0'),c=getchar();
	return kkk*x;
}
int n,zone[1001][2],F,maxn,ans[41],d[41];
inline void solve(int &zone,int &bj,int &ans,int reduce,int type)
{
	if(zone<0)
	{
		zone=-zone;
		bj^=1;
	}
	zone-=reduce;
	ans=type-bj;
}
inline void print(int p)
{
	switch(p)
	{
		case 0:putchar('D');break;
		case 1:putchar('U');break;
		case 2:putchar('L');break;
		case 3:putchar('R');break;
	}
}
int main()
{
	n=read();
	for(register int i=1;i<=n;++i)
	{
		zone[i][0]=read();
		zone[i][1]=read();
		maxn=max(abs(zone[i][0])+abs(zone[i][1]),maxn);
	}
	for(register int i=2;i<=n;++i)
		if((abs(zone[i][0])+abs(zone[i][1]))%2!=(abs(zone[i-1][0])+abs(zone[i-1][1]))%2)
		{
			puts("-1");
			return 0;
		}
	if((zone[1][0]+zone[1][1])%2==0)
	{
		F=1;
		--maxn;
	}
	int LOG=ceil(log2(maxn+1))-1;
	printf("%d\n",LOG+1+F);
	d[0]=1;
	for(register int i=0;i<=LOG;++i,d[i]=d[i-1]*2)
		printf("%d ",d[i]);
	if(F)
		putchar('1');
	putchar('\n');
	for(register int i=1;i<=n;++i)
	{
		int x=zone[i][0],y=zone[i][1],mem=-1,bjx=0,bjy=0;
		if(F)
		{
			if(abs(x)>abs(y))
				solve(x,bjx,mem,1,3);
			else
				solve(y,bjy,mem,1,1);
		}
		for(register int j=LOG;j>=0;--j)
			if(abs(x)>abs(y))
				solve(x,bjx,ans[j],d[j],3);
			else
				solve(y,bjy,ans[j],d[j],1);
		for(register int j=0;j<=LOG;++j)
			print(ans[j]);
		if(F)
			print(mem);
		putchar('\n');
	}
	return 0;
}

标签：10,int,题解,Arms,leq,solve,序列,include,ARC103D
来源： https://www.cnblogs.com/zhy12138/p/15690813.html