首页 > 其他分享> > 【六、树与二叉树】6.1树的基本概念

【六、树与二叉树】6.1树的基本概念

2021-12-05 19:32:24 作者：互联网

一、树的定义

二、基本术语

三、树的性质

性质一：树的总边数=树的所有结点的度数之和

性质二：树的结点数=树的所有结点的度数之和（树的总边数）+1

性质三：度为m的树，第i层上至多有个结点（i>=1）

一、树的定义

在我们生活中，树形思维导图和电脑里的文件夹等都属于树形结构

树是一种非线性的数据结构（一对多）

树由若干结点构成（N个）

N = 0 空树
N != 0 由唯一的根结点和若干个不相交的子树组成（每个子树也是一个树【递归定义】）

注意子树不能相交，有相交的子树整体就不是树结构了，结构就变成了图。

关于树的定义的几点说明：

①树是一种逻辑结构，也是一种分层结构

②树的根结点没有前驱结点

③除根结点外的结点，有且只有一个前驱结点

④树中所有结点可以有零个或多个后继结点

⑤树适合于表示具有层次结构的数据

⑥树中每个结点（除根结点），与上层一个结点有直接关系（边）

⑦n个结点的树，有n-1条边

例子：

A是树的根节点，B、C、D是子树的根结点

二、基本术语

我们以下面这张图来掌握树的基本术语

（1）结点

A、B、C···都是结点

结点内容由数据元素和指向子树的分支组成

例子：结点A包含数据元素A和3个指向子树的分支

（2）结点的度

结点拥有的子树的个数（分支的个数）叫作结点的度

例子：结点A的度为3

（3）树的度

树中各结点度的最大值

例子：上图中树的度为3（结点A、结点D）

（4）叶子结点

又叫作终端结点，叶子结点指度为0的结点

例子：F、G、I、J、K、L、M结点

（5）非终端结点

又叫作分支结点，指度不为0的结点

例子：A、B、C、D、E、H结点

（6）内部结点

除了根结点外的非叶子结点

例子：B、C、D、E、H结点

（7）孩子

某个结点的直接后继（可以有多个）

例子：结点A的孩子有B、C、D结点

（8）双亲

某个结点的直接前驱是它的双亲（只有一个）

例子：B、C、D结点的双亲都是A结点

（9）兄弟

拥有同一个双亲的结点之间互为兄弟

例子：B、C、D结点互为兄弟

（10）祖先

从某结点开始到根结点的路径上的所有结点，叫作该结点的祖先

例子：K的祖先为E、B、A结点

（11）子孙

以某结点为根的子树中的所有结点是该结点的子孙

例子：D的子孙为H、I、J、M结点

（12）层次

根为第一层，每向下一次增加一层

例子：上图中树的层次为4

（13）路径

两个结点的路径是由这两个结点之间所经过的结点序列构成的

例子：A、J结点之间的路径为（A、D）、（D、J）

（14）路径长度

路径上所经过的边的个数

例子：A、J结点之间的路径长度为2

（15）树的路径长度

树的路径长度是从树根到每个结点的路径长度的总和

具体学习与对比在哈夫曼树处

（16）结点的高度（该结点->叶子结点）

从该结点出发到达叶子结点，最长路径上的结点数为该结点在树中的高度

根结点的高度为树的高度

例子：结点J的高度为1

（17）结点的深度（根->该结点）

从根结点到该结点路径上的结点数

例子：结点J的深度为3

（18）树的高度、深度

结点的最大层次

例子：上图中树的高度（深度）为4

（19）堂兄弟

双亲在同一层的结点互为堂兄弟

例子：G、H结点互为堂兄弟

（20）有序树

树的左右子树不可交换的树【交换后不是同一棵树】

（21）无序树

树的左右子树可以交换的树【交换后仍然是同一棵树】

（22）森林

由若干棵互不相交的树组成的集合

例子：

★由于上面的术语记忆很杂乱，为大家准备了一张有趣的彩图，以助大家记忆理解★

三、树的性质

性质一：树的总边数=树的所有结点的度数之和

结点的度：结点拥有的子树的个数（分支的个数），叫作结点的度

原理：每个度都会对应一条边

例子：

性质二：树的结点数=树的所有结点的度数之和（树的总边数）+1

原理：1个结点有0条边、2个结点有1条边、···、n个结点有n-1条边

例子：

性质三：度为m的树，第i层上至多有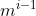 $m^{i-1}$ 个结点（i>=1）

树的度：树中各结点的度的最大值作为这棵树的度，可以有多个结点的度都是这个最大值

至多：当所有结点（除叶子结点）的度都是这个最大值时，叶子结点只出现在最后一层时，树的每一层的结点数达到最多

原理：第1层有1个结点、第2层有m个结点、第3层有 $m^{2}$ 个结点、···、第h层有 $m^{h-1}$ 个结点

例子：

性质四：高为h的m叉树至多有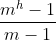 $\frac{m^{h}-1}{m-1}$ 个结点

至多：当所有结点（除叶子结点）的度都是这个最大值时，叶子结点只出现在最后一层时，树的每一层的结点数达到最多

原理：第1层有1个结点、第2层有m个结点、第3层有 $m^{2}$ 个结点、···、第h层有 $m^{h-1}$ 个结点，等比数列求和，结果为 $\frac{m^{h}-1}{m-1}$

例子：

性质五：具有n个结点的m叉树的最小高度为 $\left \lceil \log _{m}\left [ n\left ( m-1 \right )+1 \right ] \right \rceil$

证明：

四、树的存储结构

在大量的应用中，人们曾使用多种形式的存储结构来表示树。这里，我将介绍3种常用的链表结构

1.双亲表示法

前言：虽然后继的数量不确定，但是直接前驱只有一个呀！注意根没有直接前驱

实现：一维数组+结构体

结构体属性
data 数据域，存储该结点的内容
parent 指针域，存储该结点的双亲在数组中的下标（根节点的双亲下标为-1）

存储结构描述：
//结点
typedef struct {
	ElemType data;
	int parent;
}PTNode;

#define MAX_TREE_SIZE 100
//树
typedef struct {
	PTNode nodes[MAX_TREE_SIZE]; //存储结点的数组
	int n;      //真实结点数
}PTree;
例子：

特点：容易找到双亲结点，所用的时间复杂度为O(1)；找孩子要遍历整个结构才行，比如找A结点的孩子需要遍历整个数组，找到所有parent值为0的结点

2.孩子表示法

方案一：孩子存储结构存储

前言：双亲表示法存储的是双亲，向上查找；孩子存储结构存储的是孩子，向下查找

结点内容：

结点内容
data 数据域
child 指向所有孩子的指针域，按照树的度设计结点的孩子结点指针域个数

例子：

特点：存储空间不能充分利用，会造成一些浪费（指针域）

方案二：孩子链表表示法

实现：孩子链表表示法是将每个结点的孩子结点都用单链表链接起来形成一个线性结构；n个结点就有n个孩子链表（叶子结点的孩子链表为空表）

例子：

特点：寻找孩子的操作非常直接；寻找双亲需要遍历n个孩子链表，比如找H结点的双亲，需要遍历所有孩子链表，找到H结点出现的那个链表，对应数组的值就是它的双亲

和孩子链表表示法相似的存储方式：图的邻接表表示法，稀疏矩阵的邻接表表示法

3.孩子兄弟表示法

每个结点设计三个域：①数据域②第一个孩子结点指针域③下一个兄弟结点指针域

存储结构描述：
typedef struct CSNode {
	ElemType data;  //数据域
	struct CSNode* firstchild,     //指向第一个孩子的指针
		         * nextsibling;    //指向下一个兄弟的指针
}CSNode, * CStree;
例子：

特点：可以方便地实现树转二叉树，抑郁查找结点的孩子，查找双亲麻烦

标签：结点,孩子,存储,表示法,例子,双亲,二叉树,6.1,基本概念
来源： https://blog.csdn.net/m0_62516234/article/details/121731213

N = 0	空树
N != 0	由唯一的根结点和若干个不相交的子树组成（每个子树也是一个树【递归定义】）

结构体属性
data	数据域，存储该结点的内容
parent	指针域，存储该结点的双亲在数组中的下标（根节点的双亲下标为-1）

结点内容
data	数据域
child	指向所有孩子的指针域，按照树的度设计结点的孩子结点指针域个数