首页 > 其他分享> > 广义线性模型GLM

广义线性模型GLM

2021-11-16 21:03:44 作者：互联网

广义线性模型GLM

广义线性模型GLM
感谢

判断标准非常简单，响应变量y独立则GLM，否则GLMM。这就是最本质的判断标准，其它的标准都是基于这个标准来的

指数分布族

概率密度为

\[f_X(x;\theta) = h(x) e^{ (\ \eta(\theta)\cdot T(x)+A(\theta)\ )} \]

其中

$\eta(\theta)$被称为这个分布的自然参数(natural parameter )

$T(x)$为充分统计量(sufficient statistic) ，通常 $T(x)=x$

$A(\theta)$为累计函数(cumulant function) ，作用是确保概率和$\sum f(x;\theta)$为1

$h(x)$为 underlying measure

当 $T,A,h(y)$固定之后就确定了指数分布族中的一种分布模型，就得到了以$\eta$为参数的模型

还有两个等价的形式

\[f_X(x|\theta) = h(x) g(\theta) e^{(\ \eta(\theta)\cdot T(x) \ )} \\ f_X(x|\theta) = e^{(\ \eta(\theta)\cdot T(x)+ A(\theta) \ )} \]

其实，大多数概率分布都属于指数分布族：

伯努利分布（Bernouli）：对0,1问题进行建模
二项分布(Multinomial): 对K个离散结果的事件建模
泊松分布(Poisson)
指数分布(exponential)和伽马分布(gamma)：
高斯分布(Gaussian)
$\cdots$

指数分布族中常用的分布

求解的方法就是将概率分布符合指数分布族的转换成它对应的指数分布族的形式，求出指数分布族对应位置上的参数即可求出原模型的参数。

伯努利分布 Bernoulli

伯努利分布是假设一个事件只有发生或者不发生两种可能，并且这两种可能是固定不变的。那么，如果假设它发生的概率是 p，那么它不发生的概率就是 1-p。这就是伯努利分布。
伯努利实验就是做一次服从伯努利概率分布的事件，它发生的可能性是 p，不发生的可能性是 1-p。

$X$ $1$ $0$

$P$ $p$ $1-p$

\[f(x|p)=p^xq^{1-x} \]

\(X\)	\(1\)	\(0\)
\(P\)	\(p\)	\(1-p\)

我们来通过对伯努利的分布函数进行变形来展示伯努利分布是指数分布族中的一员

\[\begin{aligned} P(x; p) &= p^x(1-p)^{(1-x)} \\ &= e^{log p^x} \cdot e^{log(1-p)^{1-x}} \\ &=e^{xlog p+(1-x)log(1-p)} \\ &=e^{xlog\frac{p}{1-p}+log(1-p)} \end{aligned} \]

这就和$f_X(x;\theta) = h(x) e^{ (\ \eta(\theta)\cdot T(x)+A(\theta)\ )}$的形式归为一致了

也就是说，我们选择

$\eta (\theta)=log\frac{p}{1-p}$作为自然参数

$T(x)=x$

$A(\theta)=log(1-p)=log(1+e^\eta(p))$

$h(x)=1$

时，指数分布族就是伯努利分布

泊松分布 Poisson

泊松分布的概率函数为

\[P(X=k) = \frac{\lambda^k}{k!}e^{-\lambda},k=0,1\cdots \]
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算。

\[\begin{aligned} p(x|\lambda) &= \frac{\lambda^xe^{-\lambda}}{x!} \\ &=\frac{1}{x!}e^{log \lambda^x} \cdot e^{-\lambda} \\ &= \frac{1}{x!}e^{xlog\lambda-\lambda} \end{aligned} \]

因此，泊松分布也属于指数分布族，其相关参数为

$\eta({\theta} )= log \lambda $

$T(x)=x$

$A(\theta) = \lambda = e^\eta$

$h(x)=\frac{1}{x!}$

高斯分布(正态分布) Gaussian

单高斯分布的公式

\[p(x;\mu,\delta) = \frac{1}{\sqrt{2\pi \delta^2}} exp(-\frac{(x-\mu)^2}{2\delta^2}) \]
参数$\mu$代表样本均值， $\delta$表示样本的标准差

\[\begin{aligned} p(x) &= \frac{1}{\sqrt{2\pi \delta^2}} e^{-\frac{(x-\mu)^2}{2\delta^2}} \\ &= \frac{1}{\sqrt{2\pi \delta^2}} exp(-\frac{(x-\mu)^2}{2\delta^2}) \\ &= \frac{1}{\sqrt{2\pi }} exp(-log\delta-\frac{(x^2-2\mu x+\mu^2)}{2\delta^2}) \\ &= \frac{1}{\sqrt{2\pi }} exp(-log\delta-\frac{x^2}{2\delta^2}+\frac{\mu x}{\delta^2}-\frac{\mu^2}{2\delta^2}) \\ \end{aligned} \]

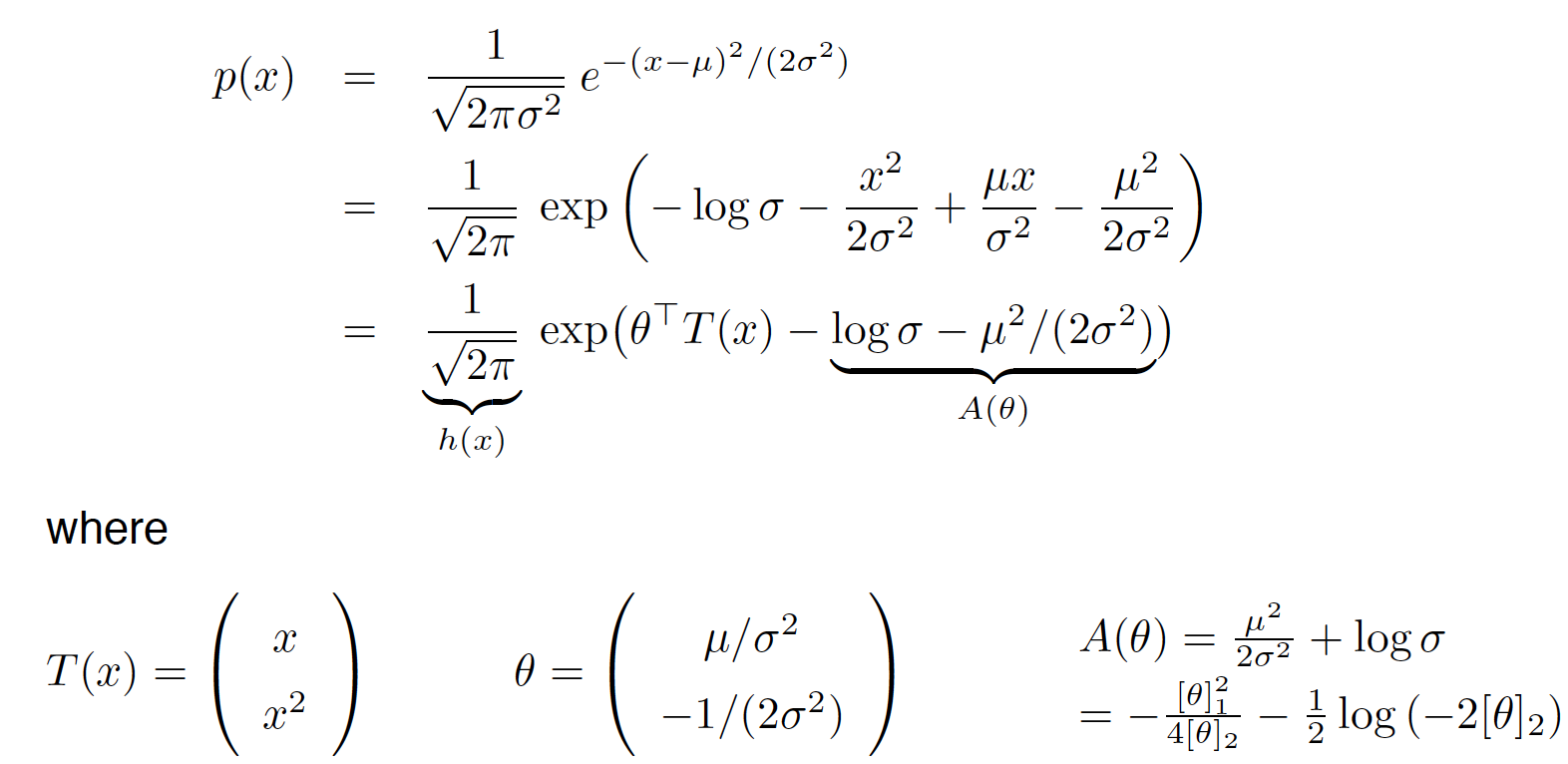
所以单变量高斯分布也属于指数分布族

多变量高斯分布

标准形式为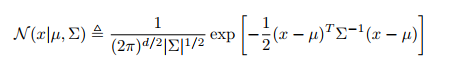多元高斯1 ：
写成指数族形式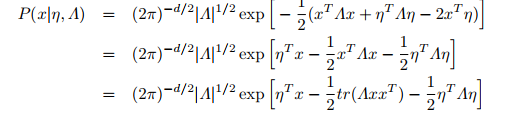：多元高斯2

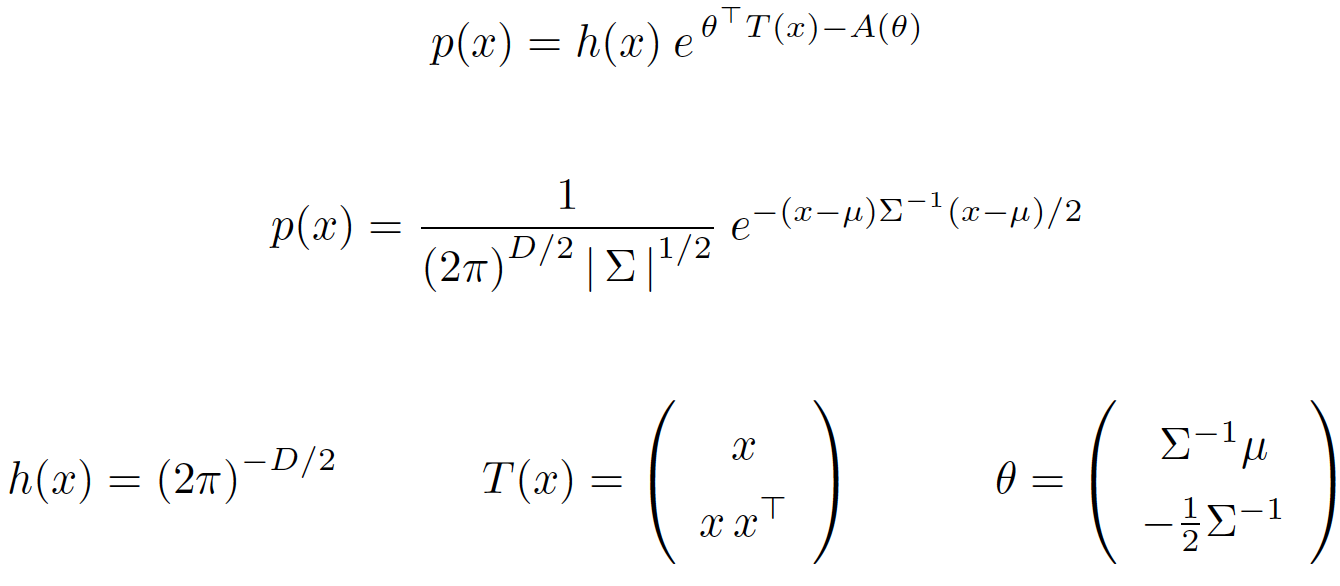
多变量高斯分布

多项式分布 Multinomial

多项式分布（Multinomial Distribution）是二项式分布的推广。

二项分布的典型例子是扔硬币，硬币正面朝上概率为p, 重复扔n次硬币，k次为正面的概率即为一个二项分布概率。把二项分布公式推广至多种状态，就得到了多项分布。

某随机实验如果有$k$个可能结局$A_1、A_2、…、A_k$，分别将他们的出现次数记为随机变量$X_1、X_2、…、X_k$，它们的概率分布分别是$p_1，p_2，…，p_k$，那么在$N$次采样的总结果中，$A_1$出现$m_1$次、$A_2$出现$m_2$次、…、$A_k$出现$m_k$次的这种事件的出现概率$P$有下面公式

\[P(X_1=m_1,X_2=m_2,\cdots,X_n=m_n)=\frac{N!}{m_1!m_2!\cdots m_n!}p_1^{m_1}p_2^{m_2}\cdots p_n^{m_n} \\ 其中，p_i\geq 0(1\leq i \leq n), p_1+p_2+\cdots+p_n=1,m_1+m_2+\cdots+m_n=N \]

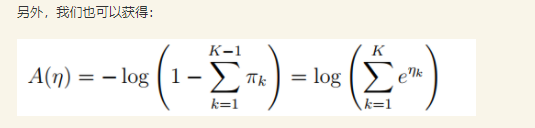
假设

为了给问题构造GLM模型，必须首先知道GLM模型的三个假设

$y|x;\eta \thicksim ExponentialFamily(\eta)$ .

比如给定样本$x$与参数$\eta$，样本的分类$y$服从以$\eta$为参数的指数分布族中的某个分布

给定$x$，广义线性模型的目标是求解$T(y)|x$ ( 即给定样本$x$的一个分类 )

不过由于很多情况下$T(y)=y$，所以我们的目标就变成了$h(x)=E[y|x;\theta]$

$\eta=\theta^T x$ .

即自然参数$\eta(\theta)$和输入$x$满足线性关系

GLM 与逻辑回归

对于二分类问题，假设$y$服从伯努利分布，满足第一个假设，即$y|x;\theta \thicksim Bernoulli(\phi)$

对于伯努利分布，我们得知 $P(y; \phi) = \phi^y(1-\phi)^{(1-y)} =e^{ylog\frac{\phi}{1-\phi}+log(1-\phi)}$

$\eta (\theta)=log\frac{\phi}{1-\phi}$作为自然参数 ,进而得到$\phi = \frac{1}{1+e^{-\eta}}$

$T(y)=y$

$A(\theta)=log(1-\phi)=log(1+e^{\eta (\theta)})$

$h(y)=1$

根据第三个假设 $\eta=\theta^T x$

我们就有

\[\phi = \frac{1}{1+e^{-\eta}} = \frac{1}{1+e^{-\theta^T x}}\\ 即 p(y=1|x;\theta) = \frac{1}{1+e^{-\theta^T x}} \]

这里的$\phi$就是伯努利分布中的概率$p$，即事件发生的概率$p(y=1)$

GLM与线性回归

在线性回归中，我们对概率分布做出的假设是服从正态分布 $y|x;\theta \thicksim N(\mu,\delta^2) $

我们可以将$\delta$设为1 ，那么则服从$y|x;\theta \thicksim N(\mu,1) $

由上面推导，我们可以得知

\[ p(y;\mu) = \frac{1}{\sqrt{(2 \pi)}} exp(-\frac{1}{2}(y-\mu)^2) \\ =\frac{1}{\sqrt{(2 \pi)}} exp(-\frac{1}{2}y^2)exp(\mu y-\frac{1}{2}\mu^2 ) \]

根据第三个假设 $\eta=\theta^T x$

于是我们就有

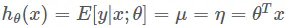
线性回归下最大似然估计与最小二乘的统一

我们发现对高斯分布做最大似然估计

感谢

https://www.jianshu.com/p/9c61629a1e7d

(10条消息) 指数分布族(Exponential Family)相关公式推导及在变分推断中的应用_qy20115549的博客-CSDN博客

https://fighterhit.oschina.io/2017/12/24/machine_learning_notes/从广义线性模型理解逻辑回归/

https://blog.csdn.net/xierhacker/article/details/53364408

标签：frac,GLM,eta,广义,delta,线性,theta,指数分布,log
来源： https://www.cnblogs.com/zuti666/p/15563535.html