0-1背包问题
作者:互联网
0-1背包问题
给定n个物品和一个背包,物品\(i\)\((1\le i \le n )\) 的重量为\(w_i\) ,其价值为\(v_i\) ,背包容量为c ,对每种物品只有两种选择:装入背包或者不装。如何选择装入背包的物品,使得装入背包的物品的总价值最大?
问题理解
刚开始是我不是很理解这个容量是什么意思,我以为是能装多少个物品的意思,事实上这个容量的意思是,这个背包所能过装的最大重量。
所以,这个题目的意思是,我这个背包只能装这么重的东西,我要怎么装,才能让我带走的东西价值最高。
思想
暴力
我们可以这么想,我们这些物品的子集全部找出来,然后再找出这些子集中重量和不超过c 的,然后从中找到价值最大的子集,然后这个子集上的东西就是我要带走的东西了。
但是,我们分析一下就会知道,对于n个物品,它的子集个数为\(2^n\) ,也就是说,它是呈指数趋势增长的,如果我们的物品很多,那这样产生的子集巨多,我们还按照上面的想法去干显然很呆。
动态规划
然后,老师教我们用动态规划去做,名词听起来就高级,然而我并不能理解动态规划是个什么思想,但这并不影响我去做这道题。也许学多一点以后就会知道了吧。那下面说一下我理解的思路:
我们把这些物品的重量用一个数组存起来,记为\(w[i]\)
把它们对应的价值也用一个数组存起来,记为\(v[i]\)
先找出最大价值是多少
那下面我们先不考虑选哪些物品的问题,先找出这个最大的价值。
我们这样子定义val(i,j) ,它表示将i 个物品装入容量为j 的背包所获得的最大价值,至于装哪些东西进背包才能获得最大价值,这就需要我们进行决策了。很明显,这是我们01背包问题的一个子问题。我们假设前i-1个物品已经决策好了,现在来决策第i个物品,那我们现在是不是就只要考虑要不要把i 装入背包就行了?如果把它装入背包后的价值变大,那我自然是把它装进来呀,是吧。好,那么我们写一下在第i 个位置的决策情况,我们来分析装和不装的情况下的价值:
- 如果当前剩余的容量\(<w[i]\),不能装入,当前价值等于前
i-1个物品决策出来的价值,即\(val(i-1,j)\) - 如果剩余容量\(>w[i]\),我可以有装入
i和不装这两种选择,我选哪种呢?那肯定做出价值大的那个选择。如果不装的话,当前价值就是:\(val(i,j)=val(i-1,j)\) ,也就是当前价值等于前i-1个物品决策出来的价值。如果选的话,那\(val(i,j)=val(i-1,j-w[i])+v[i]\) ,那当前价值相当于把前i-1个物品装入j-w[i]容量的价值加上这个物品的价值。然后我们取上面两种情况中价值大的作为决策依据。
也就是说,对第i 个物品决策时,我的价值的情况如下:
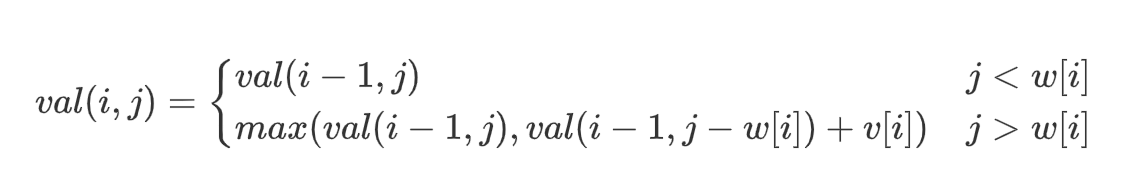
好,那我现在得到一条递推式了,我自然而然的就可以推出第i+1 个物品在背包剩余容量已知的情况下的最佳决策,第i+2个物品的在背包剩余容量已知的情况下的最佳决策········一直可以推出,有n 个物品,已知背包剩余容量为c 的情况下的最佳决策,也就是最大价值,这是不是也就解决了我的问题?
其实还有一个问题没有解决,那就是我上面这条公式的起始情况是什么?
不难发现,当我们决策第1 个物品时,我们要依赖前0个物品的决策结果,那我们来看第0个物品怎么决策的,现在有0个物品,要把它们装进容量为j 的背包,怎样装才能价值最大?显然无论怎么装,价值都是0。
还有类似的,我有i 个物品,把它们装入到容量为0的背包,价值当然也是0。那么,起始情况如下:
val(0,j)=0;
val(i,0)=0;
那由上面的递推关系,我们就可以求得\(val(n,c)\)的值了。
判断那些物品被装入了背包
上面我们的到了决策的最大价值,那下面我们来看看到底那些物品被我们装入了背包:
我们回顾上面的内容,我们会发现,对于每一个val(i,j)的值,我是不是都可以通过前一个物品的决策结果得到,也就是说,对于每一个val(i,j) ,我是不是都要存着,方便下一个物品决策时参考?那我们用一个二维数组来存它们就刚刚好。
那经过上面那些决策,我们的二维数组val[n+1][c+1]是不是就已经填好了?注意了,我这里数组大小为什么是n+1和c+1 ,因为我们上面把第0个物品和背包容量为0,都算作正常情况,那0个物品也算作一种情况。当然,你也可以把它看作是一种初始化,我这么讲是为了方便理解。
好,那我的二维表已经填好了。那我们来判断第i 个物品有没有装入到背包中,那我们是不是可以比较一下前i-1个物品在背包容量为j时决策所得的价值和前i 个物品在同种情况下的价值大小?如果val(i,j)=val(i-1,j)是不是说明,第i个物体没有被装入背包啊,因为如果装入的话,它的价值应该是比前一个大的。那么,我从后往前推是不是就可以判断出哪些物品被装入了背包,哪些没有?那到此为止,问题就解决了。
代码
#include <cstring>
#include <iostream>
using namespace std;
int main() {
int n, c;
cin >> n >> c;
int w[n], v[n];
int val[n + 1][c + 1];
memset(val, 0, sizeof(val)); //val(0,j)=val(i,0)=0,这里全初始化为0了
for (int i = 1; i <= n; i++) {
cin >> w[i];
}
for (int i = 1; i <= n; i++) {
cin >> v[i];
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= c; j++) {
if (j < w[i])
val[i][j] = val[i - 1][j];
else
val[i][j] = max(val[i - 1][j], val[i - 1][j - w[i]] + v[i]);
}
}
int x[n];
for (int j = c, i = n; i > 0; i--) {
if (val[i][j] > val[i - 1][j]) {
x[i] = 1;
j = j - w[i]; //判断被装入了,减掉它的容量,用于判断前面的物体是否被装入
} else
x[i] = 0;
}
cout << val[n][c] << endl;
for (int i = 1; i <= n; i++) {
cout << x[i] << " ";
}
return 0;
}
时间复杂度
主要算那个二重循环那里,时间复杂度就是: \(O(n*c)\)
相关题目
在acwing 上,我刚好看到一道01背包的简单题,和上面的题目一样。感觉懂了的话可以去当作练习试一下,题目链接:https://www.acwing.com/problem/content/2/
参考内容
链接:https://space.bilibili.com/501486236?spm_id_from=333.788.b_765f7570696e666f.1
特别感谢这个老师的讲解,让我理解了背包问题的解决过程,如果看不懂这篇博客的话,可以去看看这个视频
总结
- 经过这篇博客的写作,我好像有一点理解动态规划是个什么概念了,大概就是当前的决策问题要依靠前面的决策结果才能作出决策,然后通过递推关系式能够得到最终的结果,这个好像又有点像递归,有点分不清。我想大概思想就是尽可能地利用中间过程的结果为下一步决策。具体的还没有搞懂。
- 虽然有点理解背包问题了,但是用文字描述出来总感觉怪怪的,好像就是有点表达不清楚的样子,尤其是推最大价值那部分。希望以后能进一步改进一下,有大佬理解的话还希望能够点拨一下,万分感谢。
- 在编码过程中要注意对数据进行初始化,不然会有你意想不到的结果,还有就是数组不要越界,这同样会发生不可预估的错误。在定义和使用
w[n]和v[n]以及val[n+1][c+1]时尤其要注意,从+1这个操作应该就会想到了。
标签:背包,val,装入,决策,问题,物品,价值 来源: https://www.cnblogs.com/yongcheng137blogs/p/15527166.html