浅谈支配树(Lengauer - Tarjan Algorithm)
作者:互联网
他们迂回误会,我却只由你支配
问世间,哪有更完美
---《牵丝戏》
【前言】
-
本文内容主要参考 cz_xuyixuan 的博客【学习笔记】支配树。
-
笔者在原文的基础上,修改了格式,修正了一些表述不清晰的语句,在不改变原意的情况下对推导部分进行了化简,并增加了图例与自己的部分理解。
-
笔者水平有限,如有纰漏请各位指教,若有疑问,请私信。
【问题引入】
给定单源有向图 \(G\),假定起点为 \(r\) ,对于每个点 \(w\),若存在点 \(d\) 满足删去 \(d\) 后 \(r\) 与 \(w\) 不连通,即所有 \(r\) 到 \(w\) 的路径都经过 \(d\) ,则称 \(d\) 支配 \(w\) , \(d\) 是 \(w\) 的一个支配点,求出每个点能支配多少个点。
【支配树简介】
如果点 \(w\) 的一个支配点 \(i\) 满足 \(i\) 被 \(w\) 的所有其他支配点支配,则称 \(i\) 为 \(w\) 的最近支配点 ( \(immediate\) \(dominator\) ),记作 \(idom(w)\),容易发现,支配关系定义了支配点集合上的一个全序(反对称性与传递性),因此一个点的 \(idom\) 是唯一的。
对于所有非起点的点 \(w\) , \(idom(w) \to w\) 构成的图 \(G'\) 是一棵树,每个点支配其子树中的所有点,我们称 \(G'\) 为 \(G\) 的支配树。
下面介绍的 Lengauer - Tarjan 算法可以 以 \(O(n\log n + m)\) 的时间,\(O(n + m)\) 的空间求解支配树。
【前置知识】
Dfs 序相关知识,如果学习过 Tarjan 求强连通分量是更好的。
【记号与约定】
-
点的比较基于 Dfs 序大小。
\(V\) 表示点集, \(E\) 表示边集。
\(a \to b\) :\(a\) 通过一条边直接到达 \(b\) 。
\(a ⇝ b\) : \(a\) 通过某条路径达到 \(b\)。
-
完全祖先:一个点在 Dfs 树上所有不含它自身的祖先。
半支配点(\(semi\) \(dominator\)):点 \(w\) 的半支配点定义为所有 \(v\) 中满足 \(v ⇝ w\) ,且路径上的点均大于 \(w\) 中最小的一个,记作 \(sdom(w)\) ,这也是 Lengauer - Tarjan 算法的核心。
-
\(p(x)\):标号为 \(x\) 的点。
\(b(x)\):有边直接连到 \(x\) 的点集。
\(c(x)\):\(sdom\) 为 \(x\) 的点集。
-
数组的下标默认使用点在原图中的标号。
\(idom\) 和 \(sdom\) 数组使用点的 Dfs 序标号。
【定理推导】
-
引理 \(1\) :若两个点 \(u,v\) 满足 \(u \leq v\) 那么任意 \(u\) 到 \(v\) 的路径经过两者在 Dfs 树上的公共祖先。
证明 : 考虑删去所有 \(u,v\) 的公共祖先,那么两者分列两颗子树。 前向边与有向边均无法跨越子树,而横叉边需要满足 \(v \leq u\),这说明了原来的可达路径依赖于 \(u,v\) 的公共祖先。
-
引理 \(2\) :\(idom(u)\) 为 \(u\),\(u \neq r\) 的完全祖先。
证明 : 依照定义即得。
-
引理 \(3\) :\(sdom(u)\) 为 \(u\) , \(u \neq r\) 的完全祖先。
证明: 根据定义, \(fa_u\) 是 \(sdom(u)\) 的一个候选,于是有 \(sdom(u) \leq fa_u\),利用引理 \(1\) 可知,若 \(sdom(u)\) 与 \(u\) 不在某个相对的同一子树中,那么它们之间的路径必然经过一个公共祖先,而公共祖先的 Dfs 序小于 \(u\) ,这显然是不合法的。
-
引理 \(4\) :\(idom(u)\) 为 \(sdom(u)\) 的祖先。
证明: 反之存在路径 \(r\) (为 \(sdom(u)\) 的祖先)\(⇝ u\) 而不经过 \(idom(u)\) ,这与定义矛盾。
-
引理 \(5\) :所有 \(idom(u)\) 到 \(u\) 的路径两两之间不交或完全包含。
证明: 我们先明确一个事实,一个点的支配点集构成 Dfs 树上的一条祖先链,这也对应了前文所叙述的最近支配点。若引理不成立,说明有一对 \((u,v)\) 使得 \(idom(u)\) 在 \(idom(v)\) 到 \(v\) 的链上,但注意到 \(idom(u)\) 是 \(idom(v)\) 的真后代,其一定不支配 \(v\),这意味着存在 \(r ⇝ v ⇝ u\) 不经过 \(idom(u)\) ,这与定义相悖。
接下来我们将通过这 \(5\) 条引理来推到一些更有效的结论,解释 \(idom\) 与 \(sdom\) 之间的关系,进而导出求解的算法,请读者再次明确前文的定义,部分证明可能较为复杂,这里给出支配树的一个示例,其中括号内数字为 Dfs 序,字母为半支配点(图源网络,侵删):
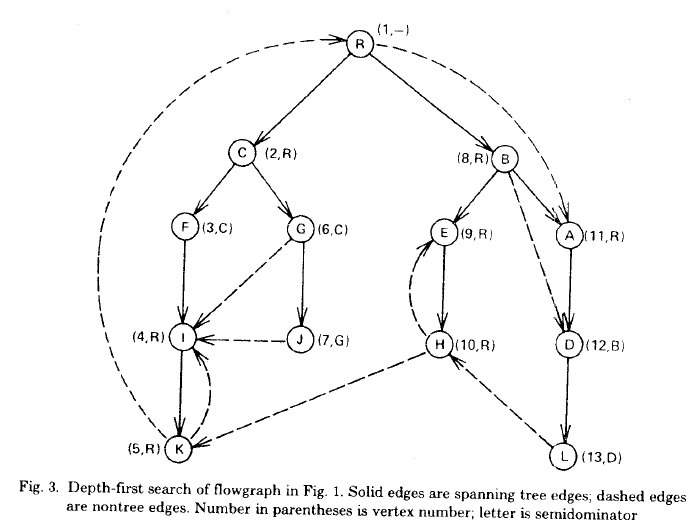
-
定理 \(1\): 对于 Dfs 树上的一条链 \(sdom(w)\) 到 \(w\) ,若链上所有点 \(u\) 均满足 \(sdom(w) \leq sdom(u)\),那么 \(idom(w) = sdom(w)\)。
证明: 条件改写为 \(sdom(w) ⇝ w\) 完全包含 \(sdom(u) ⇝ u\) ,由引理 \(4\) 可知,\(idom(w)\) 为 \(sdom(w)\) 的祖先,只需证明 \(sdom(w)\) 支配 \(w\) , 对于任意 \(r ⇝ w\) 的路径,设路径上最后一个编号小于 \(sdom(w)\) 的点为 \(x\) ,它显然能到达 Dfs 树上 \(sdom(w)\) 到 \(w\) 这条祖先链上的一个点集,取其中最小的点 \(y\) ,依条件得 \(sdom(w) \leq sdom(y)\) ,所以 \(x \neq sdom(y)\) ,这又导出了 \(x\) 到 \(y\) 的路径上存在点 \(v\) 使得 \(x\) 是 \(v\) , \(v\) 是 \(y\) 的完全祖先,因 \(x\) 的最小性,\((sdom(w),v,w)\) 又是一条祖先链,考虑它们的编号,这与 \(y\) 的最小性矛盾, \(y\) 只能是 \(sdom(w)\),这就证明了所有 \(r\) 到 \(w\) 的路径都经过 \(sdom(w)\),命题得证。
类似地,我们可以推导出另一个结论,证明留给读者思考。
- 定理 \(2\): 对于 Dfs 树上的一条链 \(sdom(w)\) 到 \(w\) ,设 \(u\) 为链上 \(sdom(u)\) 最小的一个,若 \(sdom(u) \leq sdom(w)\) ,则 \(idom(w) = idom(u)\) 。
经过以上两个定理的推导,我们就可以利用 \(sdom\) 求解 \(idom\) 了,给出一个简单的推论:
-
推论 \(1\):设 \(u\) 为祖先链 \(sdom(w)\) 到 \(w\) 上 \(sdom(u)\) 最小的一个,则 \(idom(w) = sdom(w) \times [sdom(u) = sdom(w)] + idom(u) \times [sdom(u) < sdom(w)]\)
由于 \(w\) 是 \(u\) 的一个候选,这里必有 \(sdom(u) \leq sdom(w)\) 。
目前的主要问题是如何快速计算 \(sdom\) ,直接根据定义计算的效率不能满足我们的要求,于是引入另一个定理:
-
定理 \(3\): \(sdom(w) = min(v|(v, w) ∈ E, v < w ∪ sdom(u) | u > w,∃(v,w) ∈ E,u∈(r ⇝ v))\)
证明: 设 \(RHS = x\),易得 \(x\) 是 \(sdow(w)\) 的候选项,有 \(sdow(w) \leq x\) ,考虑任意一条 \(sdow(w)\) 到 \(w\) 且所有中转点大于 \(w\) 的路径,只有一条边的情况是平凡的,设路径上 \(w\) 的前驱为 \(last\) ,取中转点中为 \(last\) 祖先的最小的 \(p\) , \(p\) 的最小性限制了 \(sdom(w)\) 到 \(p\) 的路径中转点均大于 \(p\) ,于是 \(sdom(w)\) 是 \(sdom(p)\) 的候选,而 \(RHS\) 右侧的限制表明了 \(sdom(p)\) 是 \(x\) 的候选,于是 \(x \leq sdom(w)\) ,结合 \(sdom(w) \leq x\) ,就得到了 \(sdom(w)\) 的另一个描述。
总结一下,通过一系列偏序关系,我们得到了 \(idom\) 与 \(sdom\) 另一个完备且更为简单的定义,问题就转化为我们熟悉的树上操作了。
【算法流程】
- 算法的简要流程
\(1.\) 求 Dfs 树
\(2.\) 求解半支配点
\(3.\) 利用半支配点求解支配点
- 具体描述以及实现细节
其中 \(1\) 是平凡的,先考虑求半支配点,自然地按 Dfs 序倒序枚举,设枚举到的点为 \(u\) ,建出反图,遍历 \(u\) 的前驱,根据定理 \(3\) ,第一种情况可以直接求出,对于第二种情况,我们维护 Dfs 树上的一个带权并查集,每次处理一个点后把他合并到 Dfs 树上的父亲,同时维护一个到祖先的 \(sdom\) 最小值,记为 \(ran\)。
我们来审视一下这部分流程,由于先枚举的先标号更大,所以最新枚举到的点可以视为一个临时的根,那么定理 \(3\) 的情况 \(2\) 可以直接维护,同时,自底向上构建半支配树,对 \(idom\) 的求解也转化为了到根的 \(sdom\) 最值查询,注意到我们可以先处理一部分 \(c(x)\) 中点对 \(x\) 的影响,每次对 \(x\) 当前半支配树的儿子求一遍 \(idom\) 并删去这些儿子,最后由于定理 \(3\) 的情况 \(2\) 会出现不知道某个点的 \(sdom\) 的情况,可以直接令 \(idom\) 指向\(ran\) ,最后正序扫描一遍即可。
【代码实现】
给出一份较为简洁的代码以供参考:
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
const int N = 3e5 + 5;
int n, m, rt;
int dfn[N], p[N], fa[N], idx;
int idom[N], sdom[N], f[N], ran[N], ans[N];
std :: vector <int> e[N], g[N], tr[N];
void Dfs(int u) {
p[dfn[u] = ++idx] = u;
for (int v : e[u])
if (!dfn[v])
fa[v] = u, Dfs(v);
}
int Merge(int x) {
if (f[x] == x)
return x;
int res = Merge(f[x]);
if (dfn[sdom[ran[f[x]]]] < dfn[sdom[ran[x]]])
ran[x] = ran[f[x]];
return f[x] = res;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int u, v;
scanf("%d%d", &u, &v);
e[u].push_back(v);
g[v].push_back(u);
}
Dfs(1);
for (int i = 1; i <= n; i++)
sdom[i] = f[i] = ran[i] = i;
for (int i = idx; i > 1; i--) {
int tmp = p[i];
for (int v : g[tmp]) {
if (!dfn[v])
continue;
Merge(v);
if (dfn[sdom[ran[v]]] < dfn[sdom[tmp]])
sdom[tmp] = sdom[ran[v]];
}
f[tmp] = fa[tmp];
tr[sdom[tmp]].push_back(tmp);
tmp = fa[tmp];
for (int v : tr[tmp]) {
Merge(v);
if (tmp == sdom[ran[v]])
idom[v] = tmp;
else
idom[v] = ran[v];
}
tr[tmp].clear();
}
for (int i = 2; i <= idx; i++) {
int tmp = p[i];
if (idom[tmp] ^ sdom[tmp])
idom[tmp] = idom[idom[tmp]];
}
for (int i = idx; i > 1; i--)
ans[idom[p[i]]] += ++ans[p[i]];
ans[1]++;
for (int i = 1; i <= n; i++)
printf("%d ", ans[i]);
return 0;
}
【一些思考】
-
很大一部分支配树的应用属于“建出支配树就是另一道题了”,对其本身的结构并没有什么应用。
-
上文提到 \(sdom_x\) 到 \(x\) 的路径具有分裂的关系,这一点类似于 \(\text{SAM}\) 的 \(endpos\) 集合,如果笔者在这方面有所发现会来更新。
-
半支配树也是一个很精妙的结构。
标签:tmp,sdom,支配,浅谈,Algorithm,int,Tarjan,Dfs,idom 来源: https://www.cnblogs.com/treap/p/15412380.html