感知器

1.定义

输入多个信号输出一个信号。
例：x1，x2为输入信号。y是输出信号。w1，w2是权重，y是输出信号，Θ是阈值。高于阈值感知器被激活输出y。（权重越大说明越被看重，阈值是激活得难易度）

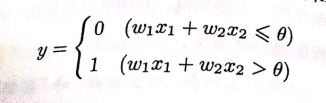
2.实例

2.1 与门

逻辑电路中的与门，就是感知器得一种，输入x1,x2得到y，真值表:

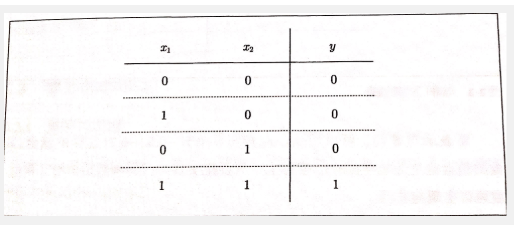
同时还有与非门(与门加非)，或门。
代码实现

def AND(x1, x2):
    w1,w2,theta = 0.5,0.5,0.7
    tmp = x1 * w1 + x2 * w2
    if tmp > theta:
        return 1
    elif tmp <= theta:
        return 0

将公式编写把Θ变为-b

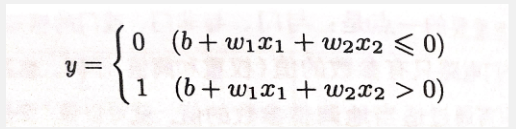
代码修改

import numpy as np
def ANDD(x1,x2):
    x = np.array([x1,x2])
    w = np.array([0.5,0.5])
    b = 0.7
    y = np.sum(x * w) - b
    if y > 0:
        return 1
    elif y <= 0:
        return 0

同样的与非们和或门也可以使用类似代码表示。
或门得图像表达：

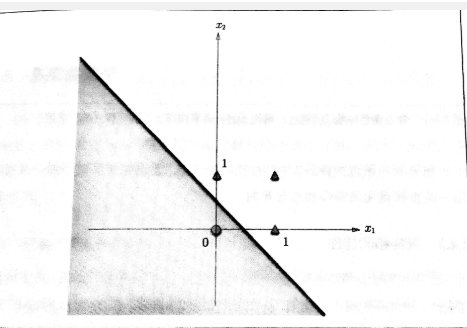
可以看到感知机是被直线分割

2.2异或门

异或门是输入得x1,x2相同为1不同为零。但是用之前的方法拟合不出来，因为他并不是线性分割。
异或门图像：

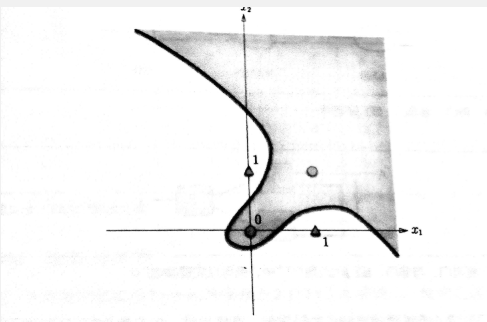
但是我们还有方法拟合，我们可以通过，利用数字电路的方式来拟合。

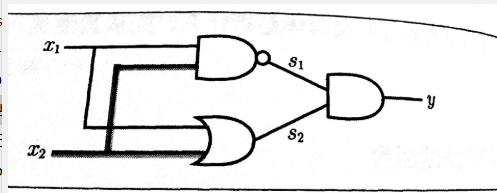
从上图可以看出，我们使用与门，与非门，或门就可以组成异或门。
真值表:

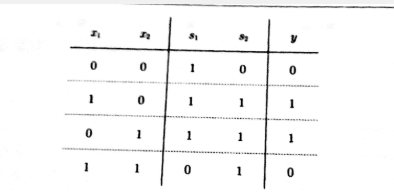
代码:

import numpy as np
def AND(x1,x2):
    x = np.array([x1,x2])
    w = np.array([0.5,0.5])
    theta = 0.7
    y = np.sum(x * w) - theta
    if y>0:
        return 1
    elif y<=0:
        return 0
def NAND(x1,x2):
    x = np.array([x1,x2])
    w = np.array([-0.5,-0.5])
    theta = -0.7
    y = np.sum(x * w) - theta
    if y > 0:
        return 1
    elif y <= 0:
        return 0
def OR(x1,x2):
    x = np.array([x1,x2])
    w = np.array([0.5,0.5])
    theta = 0.2
    y = np.sum(x * w) - theta
    if y > 0:
        return 1
    elif y <= 0:
        return 0
def XOR(x1,x2):
    y1 = NAND(x1,x2)
    print(f"NAND is {y1}")
    y2 = OR(x1,x2)
    print(f"OR is {y2}")
    y = AND(y1,y2)
    return y
print(XOR(1,1))

3.从与非门到计算机

计算机是处理信息的机器，像计算机中输入一些信息之后，会按照一定处理，输出结果。这和感知器的思路是一致的。所以理论上只要通过与非门的组合，就可以实现计算机了。推荐书籍《计算机系统要素：从零开始构建现代计算机》，通过NAND构建俄罗斯方块的计算机的过程。理论上两次感知器可以拟合任何东西，也可以用来拟合计算机，但是只有两层的话，感知器的权重很难确定。还是应该先实现各个构件在组合，如全加器，ALU等等。

标签：elif,感知器,0.5,学习,np,第二章,x2,x1
来源： https://www.cnblogs.com/wenwenjiejie/p/15367410.html