【3D数学基础:图形与游戏开发】笔记 第9章 矩阵的更多知识
作者:互联网
【3D数学基础:图形与游戏开发】笔记 第9章 矩阵的更多知识
矩阵的行列式
在任意方阵中都存在一个标量,称作该方阵的行列式。方阵M的行列式记作|M|或“detM”。非方阵矩阵的行列式是末定义的。

注意,在书写行列式时,两边用竖线将数字块围起来,省略方括号下面的示意图能帮助起记忆。将主对角线和反对角线上的元素各自相乘,然后用主对角线元素的积减去反对角线元素的积。

行列式的重要性质
- 矩阵积的行列式等于矩阵行列式的积:|AB|=|A||B|
- 这可以扩展到多个矩阵的情况:|M1M2····Mn-1Mn| = |M1||M2|···|Mn-1||Mn|
- 矩阵转置的行列式等于原矩阵的行列式:|M|T = |M|。
- 如果矩阵的任意行或列全为零,那么它的行列式等于零。
- 交换矩阵的任意两行或两列,行列式变负。
- 任意行或列的非零积加到另一行或列上不会改变行列式的值。
行列式的几何意义
2D行列式的几何意义
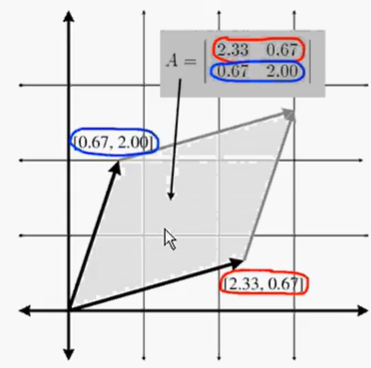
矩阵的行列式有着非常有趣的几何解释。2D中,行列式等于以基向量为两边的平行四边形的有符号面积(如图9.1所示)。我们曾介绍过如何利用平行四边形形象化显示坐标空间的变换。
有符号面积是指如果平行四边形相对于原来的方位“翻转”那么面积变负。
3D行列式的几何意义
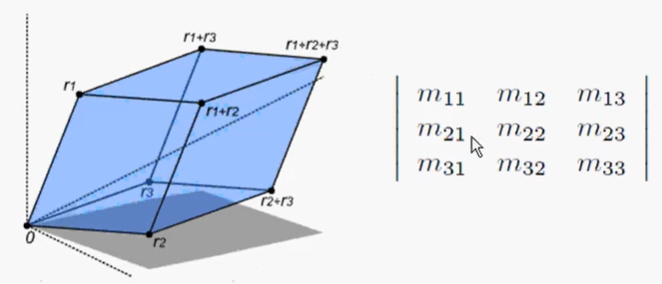
3D中,行列式等于以变换后的基向量为三边的平行六面体的有符号体积。3D中,如果变换使得平行六面体“由里向外”翻转,则行列式变负。
行列式和矩阵变换导致的尺寸改变相关。其中行列式的绝对值和面积(2D)、体积3D)的改变相关。行列式的符号说明了变换矩阵是否包含镜象或投影。
矩阵的行列式还能对矩阵所代表的变换进行分类:
- 如果矩阵行列式为零,那么该矩阵包含投影。
- 如果阵行列式为负,那么该矩阵包含镜象。
代数余子式
假设矩阵M有r行,c列。记法M|ij|表示从M中除去第i行和第j列后剩下的矩阵。显然,该矩阵有r-1行,c-1列。矩阵M|ij|称作M的余子式。考虑3×3阶矩阵M:
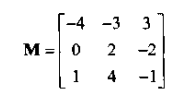
余子式M|12|是一个2×2阶矩阵,是从M中除去第1行和第2列的结果:
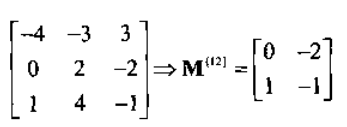
对方阵M,给定行、列元素的代数余子式等于相应余子式的有符号行列式,见公式9.3。

这个公式可能看不清楚,它是:Cij = (-1)i+j |M|ij||。
代数余子式矩阵
如上,用记法Cij表示M的第i行,第j列元素的代数余子式。注意余子式是一个矩阵,而代数余子式是一个标量。代数余子式计算式中的项(-1)(i+j)有以棋盘形式使矩阵的代数余子式每隔一个为负的效果:
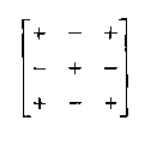
首先,从矩阵中任意选择一行或一列,对该行或列中的每个元素,都乘以对应的代数余子式。这些乘积的和就是矩阵的行列式。例如,任意选择一行,如行i行列式的计算过程如公式9.4所示。
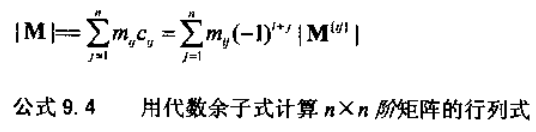
矩阵的逆
注意,只有方阵才能够求逆。
方阵M的逆,记作M-1,也是个矩阵,当M与M-1乘时,结果是单位矩阵。用公式表示为公式9.6的形式。
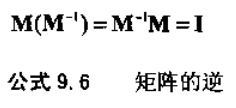
并非所有矩阵都有逆。一个明显的例子是若矩阵的某一行或列上的元素都为零,用任何矩阵乘以该矩阵,结果都是一个零矩阵。如果一个矩阵有逆矩阵,那么称它为可逆的或非奇异的。如果一个矩阵没有逆矩阵,则称它为不可逆的或奇异矩阵。奇异矩阵的行列式为零,非奇矩阵的行列式不为零,所以检测行列式的值是判断矩阵是否可逆的有效方法。此外,对于任意可逆矩阵M,当且仅当v=0时,vM0。
M的“标准伴随矩阵”记作“adM”,定义为M的代数余子式矩阵的转置矩阵。下面是一个例子:

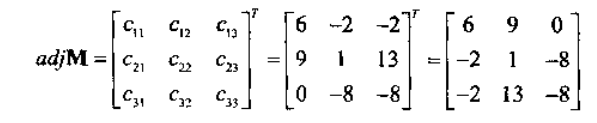

当然还有其他方法可以用来计算矩阵的逆,比如高斯消元法。很多线性代数书都断定该方法更适合在计算机上实现,因为它所使用的代数运算较少,这种说法其实是不正确的。对于大矩阵或某特殊矩阵来说,这也许是对的。然而,对于低阶矩阵,比如几何应用中常见的那些低阶矩阵,标准伴随矩阵可能更快些。因为可以为标准伴随矩阵提供无分支( branchless)实现,这种实现方法在当今的超标量体系结构和专用向量处理器上会更快一些。
矩阵的逆的重要性质
- 如果M是非奇异矩阵,则该矩阵的逆的逆等于原矩阵:(M-1)-1=M。
- 单位矩阵的逆是它本身:I-1 = I。
- 矩阵转置的逆等于它的逆的转置:(MT)-1=(M-1)T。
- 矩阵乘积的逆等于矩阵的逆的相反顺序的乘积:(AB)-1=B-1A-1。这可扩展到多个矩阵的情况:
(M1M2…Mn-1Mn)-1=Mn-1Mn-1-1M2-1M1-1。
矩阵的逆的几何意义
矩阵的逆在几何上非常有用,因为它使得我们可以计算变换的“反向”或“相反”变换。——能“撤销”原变换的变换。所以,如果向量v用矩阵M来进行变换,接着用M的逆M进行变换,将会得到原向量,除了“投影”以外。这很容易通过代数方法验证:
(vM)M-1=v(MM-1) = vI=v
正交矩阵
运算法则
若方阵M是正交的,则当且仅当M与它转置MT的乘积等于单位矩阵。检测矩阵的正交性:M正交 <=> MMT = I
回忆9.2节中的定义,矩阵乘以它的逆等于单位矩阵:MM-1 = I。
所以,如果一个矩阵是正交的,那么它的转置等于它的逆。即:
M正交 <=> MT=M-1
这是一条非常有用的性质,因为在实际应用中经常需要计算矩阵的逆,而3D图形计算中正交矩阵出现得又是如此频繁。如果知道矩阵是正交的,就可以全避免计算逆矩阵了,这也将大大减少计算量。
正交矩阵的几何意义
换句话说,对于任意矩阵M,怎样检测它是否正交?当MM=I时M是正交的。它的确切含义如下:
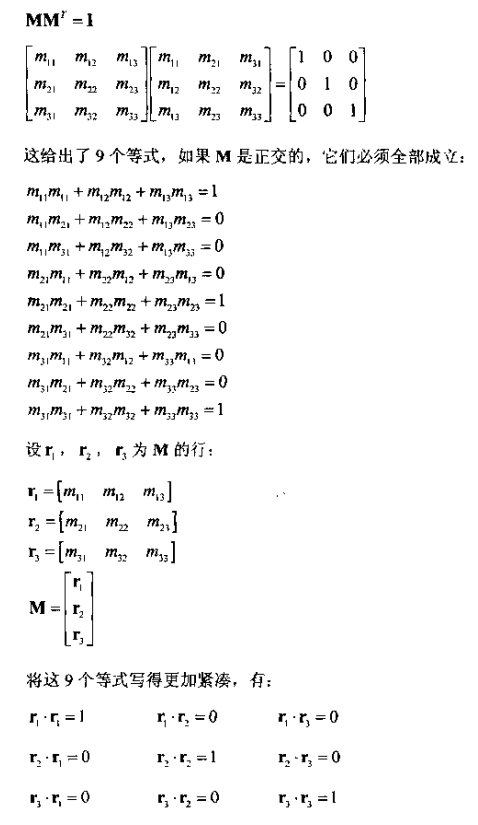
现在做一些解释:
- 当且仅当一个向量是单位向量时,它与它自身的点积结果是1。因此,仅当r1、r2、r3是单位向量时,第1、4、9式才能成立。
- 当且仅当两个向量互相垂直时,它们的点积为零。因此,仅当r1、r2、r3互柑垂直时其他等式才成立。
所以一个矩阵是正交的,必须满足以下条件:
- 矩阵的每一行都是单位向量。
- 矩阵的所有行相垂直。
- 对矩阵的列也能得到类似的条件。这使得以下结论非常清楚:如果M是正交的,则M也是止交的。
计算逆矩阵时,仅在先知道矩阵是正交的情况下才能利用正交性的优点。如果预先不知道,那么检查正交性经常是浪费时间。即使在最好的情况下,先检查正交性以确定矩阵是否正交再进行转置,和开始就进行求逆运算也将耗费同样多的时间。而如果矩阵不是正交的,那么这种检查完全是浪费时间。
注意,有个术语上的差别可能会导致轻微的混淆。线性代数中,如果一组向量互相垂直,这组向量就被认为是正交基,它只要求所有向量互相垂直,并不要求所有向量都是单位向量。如它们都是单位向量,则称它们为标准正交基。本书所讲的正交矩阵的行或列向量都是指标准正交基向量所以,本书中由组正交基向量构造的矩阵并不一定是正交矩阵(除非基向量是标准正交的)。
矩阵正交化
有时可能会遇到略微违反了正交性的矩阵。例如,可能从外部得到了坏数据,或者是浮点数运算的累积错误(称作“矩阵爬行”)。这些情况下,需要做矩阵正交化,得到一个正交矩阵,这个矩阵要尽可能地和原矩阵相同(至少希望是这样)。
构造一组正交基向量(矩阵的行)的标准算法是施密特正交化。它的基本思想是,对每一行,从中减去平行于已处理过的行的部分,最后得到垂直向量。


齐次矩阵
为什么要引入齐次矩阵
在线性变换中,所有的变换都可以用一个矩阵乘以xy的形式来表示,例如在切变中:
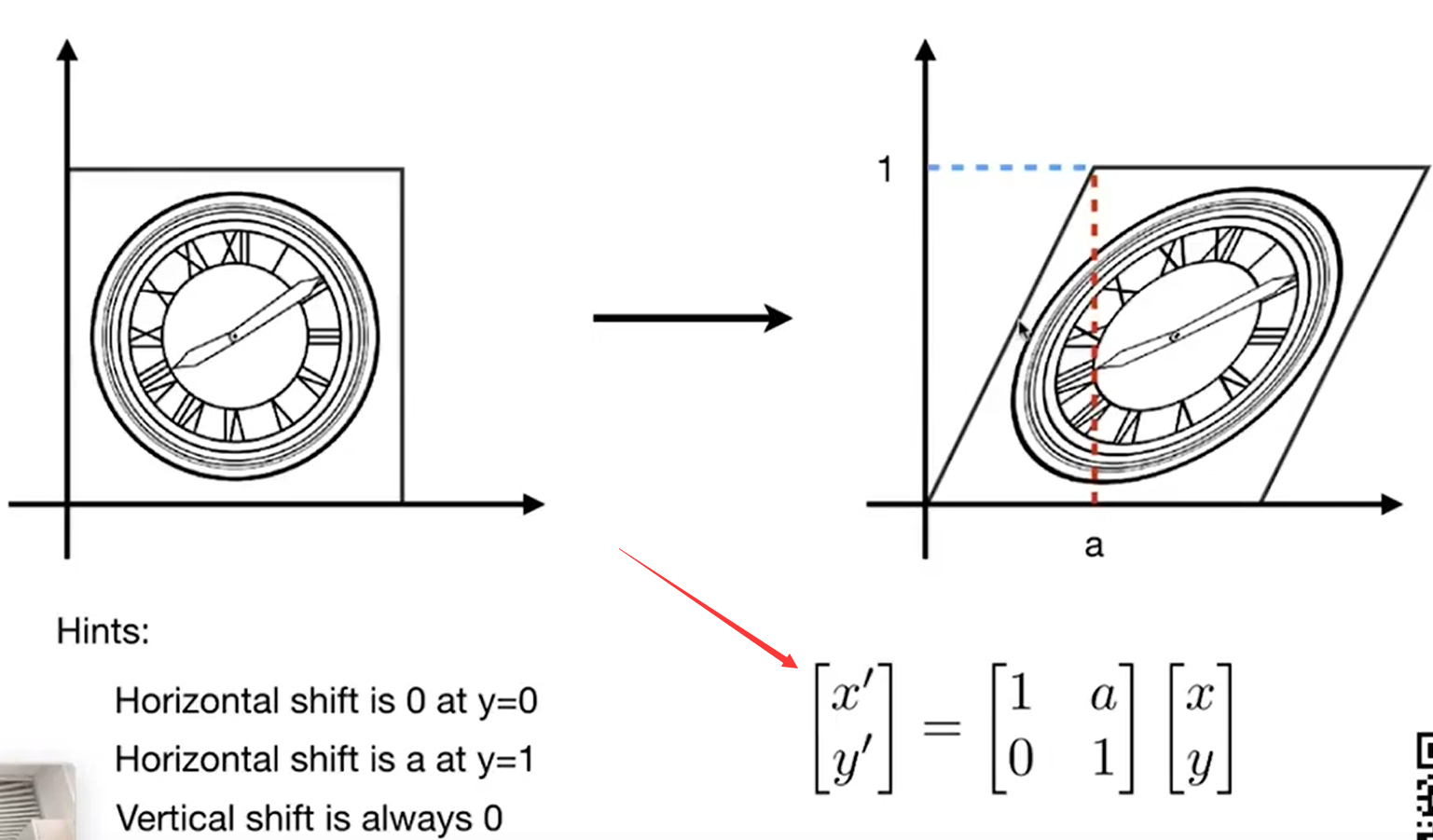
但是平移无论如何都不能写成这种形式。
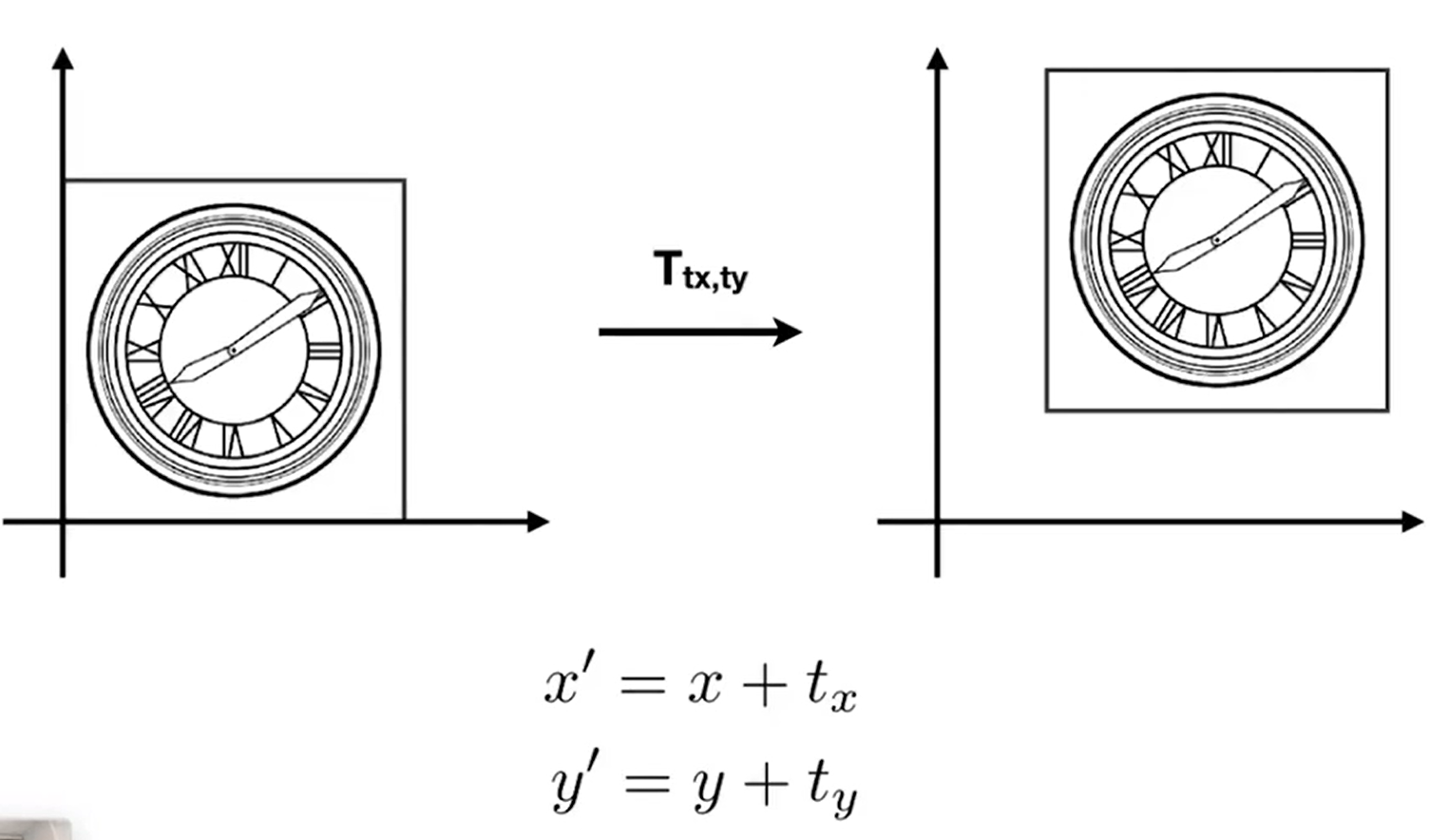
顶多写成矩阵再加上位移:

人们不希望将平移变换当作一种特殊变换来处理(相当于现在线性变换需要一个矩阵,平移又需要一个矩阵),希望它能与线性变换统一起来用一种表示方法来表示(统一以后线性变换和平移就能够写到一起了,只需要一个矩阵)。
所以就引入了齐次坐标来解决这个问题。
在计算机图形学中,坐标转换通常不是单一的,一个几何体在每一帧可能都设计了多个平移,旋转,缩放等变化,这些变化我们通常使用串接各个子变化矩阵的方式得到一个最终变化矩阵,从而减少计算量。
齐次坐标
在2D中使用齐次坐标
我们为2D中的点和向量都增加一个维度:

当W为1或者0时,操作有效。
原矩阵乘以[x,y,1]T以后就变成了x+tx和y+ty的形式,这就将平移与其他线性变换统一起来了,平移也就可以写成跟其他线性变换一样的矩阵形式了。
注意:
- 原矩阵|1 0 0 1|还是用来表示原先的线性变换,例如旋转、缩放等。
- 原矩阵中的最后一列用来表示平移,其中的tx和ty表示的就是平移。
- 在原矩阵的最后一行加上的是[0,0,1],就是为了保证变换结果与加上之前相同。
为什么新增的维度点是加上1而向量是加上0?
向量我们只关心方向,从一个地方将向量平移到另一个地方,它们还是同一个向量,我们已经在向量的几何意义中讨论过。给向量加上0是为了将向量“保护”起来,在平移之后不让它发生改变。同理,给点加上1也是一样的道理。
向量和点操作的相关解释
- 向量 + 向量 = 向量(即平移向量,这在向量的加法和减法的几何意义中已经讨论过)
- 点 - 点 = 向量(即向量)
- 点 + 向量 = 点(即点在向量上移动)
- 点 + 点 = ?(无意义)
在齐次坐标中扩展了点 + 点的意义:
在2D中,将所有的坐标都看成是x/w,y/w的形式(w!=0):
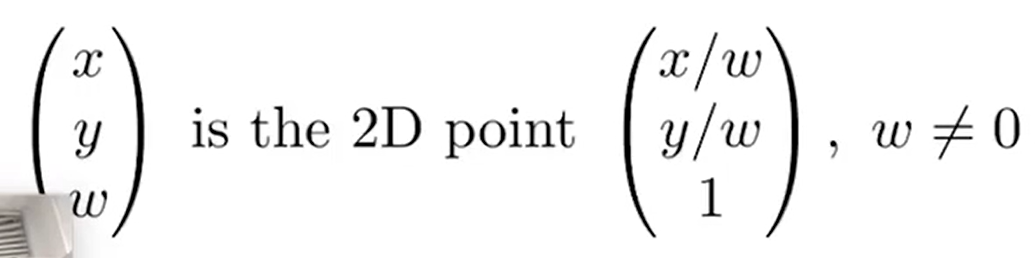
所以两个点相加时,w变为2,而怎么变回1呢?(变回1是为了保证与加w之前的表示相同)
即将w/2即可。即点 + 点 = 两点连线上的中点。
用齐次坐标统一2D变换

仿射变换用齐次坐标来表示
回顾一下:仿射变换 = 线性变换 + 平移,即:

引入了齐次坐标以后我们能将平移和其他线性变换统一起来,即:

其中|abcd|是原矩阵,用来表示原先的线性变换。
在3D中使用齐次坐标
与2D一样,在3D中也有平移,我们也希望将平移与其他线性变换统一起来。
所以用与2D类似的方法,给3D增加一个维度:
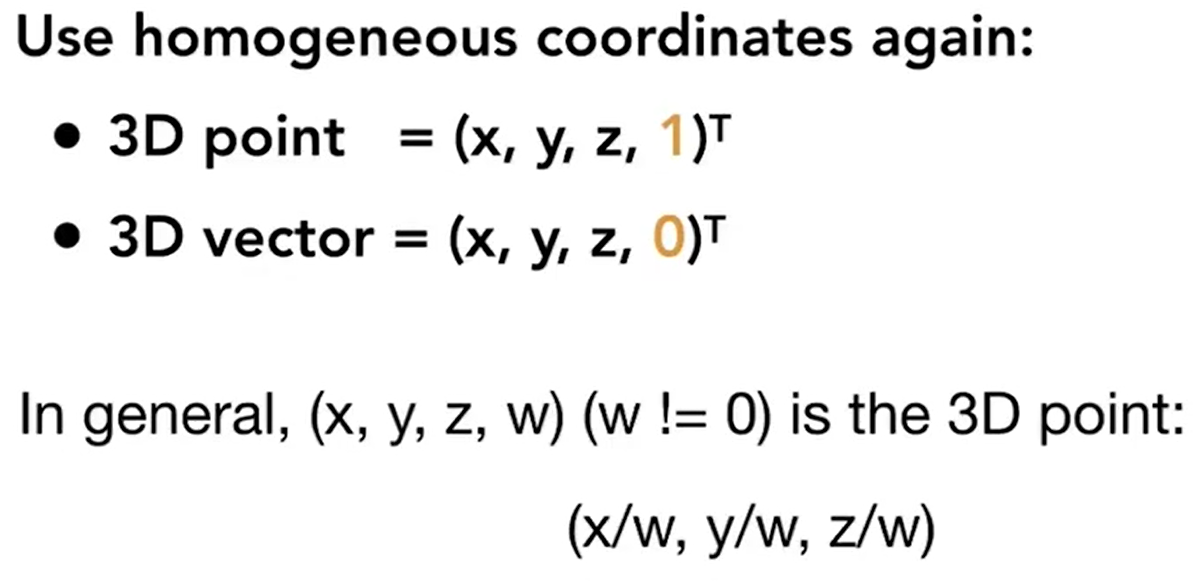
同样的,我们也在原矩阵的基础上面加上[0,0,0,1](保证结果不变),最后一列同样同来表示平移,其中tx,ty,tz为平移。

用齐次坐标统一3D变换
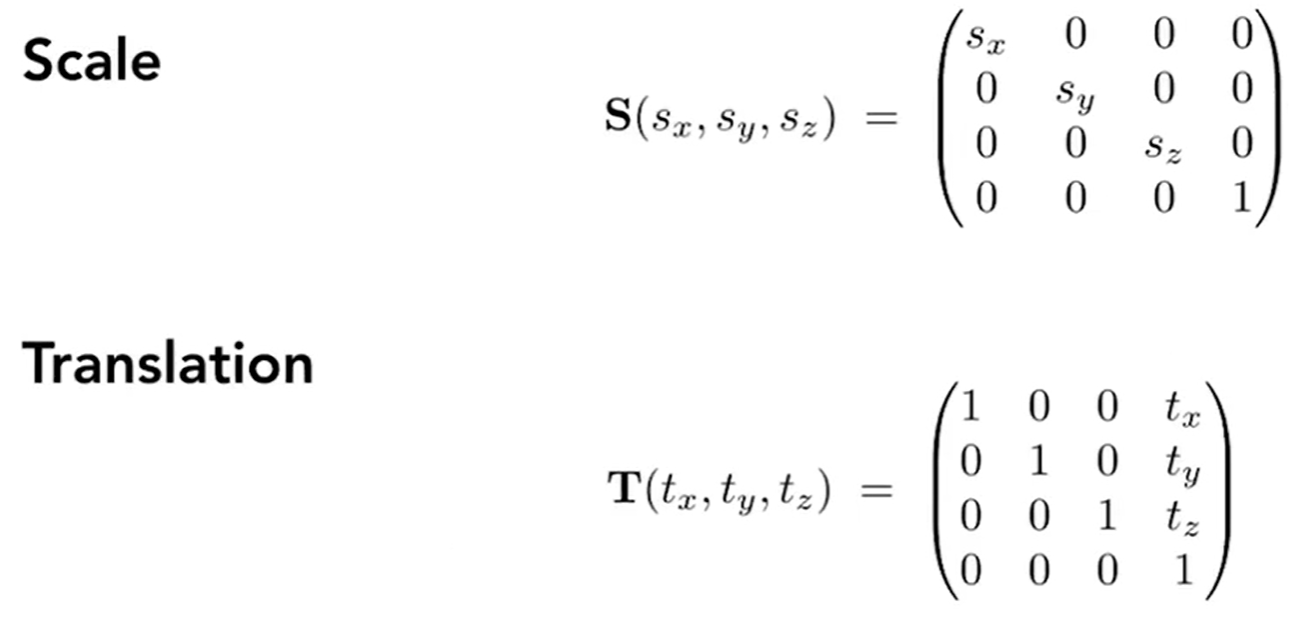
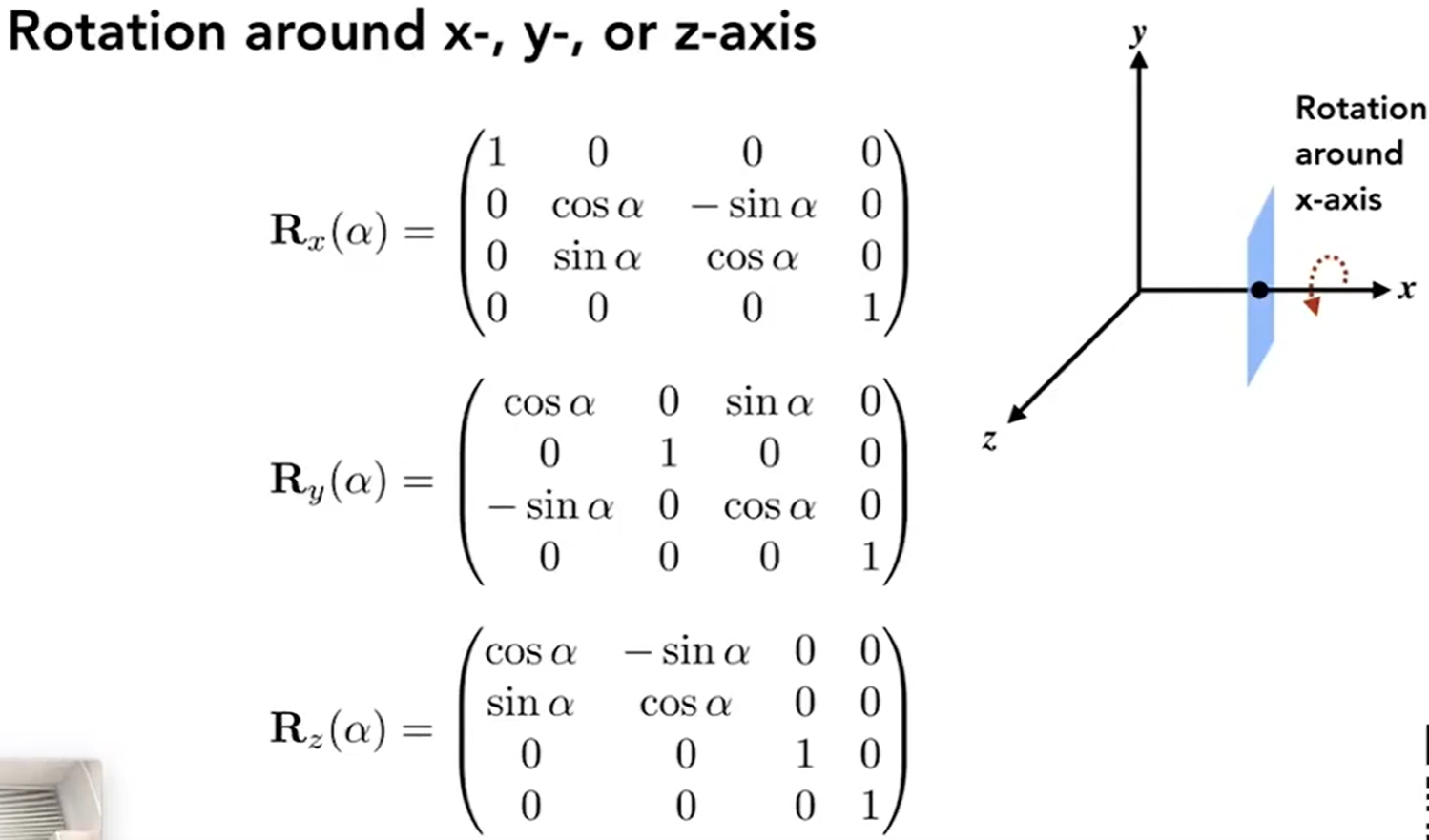
4×4平移矩阵
齐次矩阵:
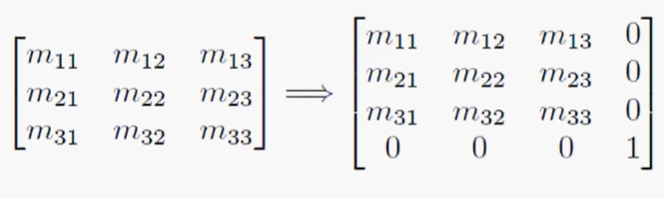
平移矩阵:
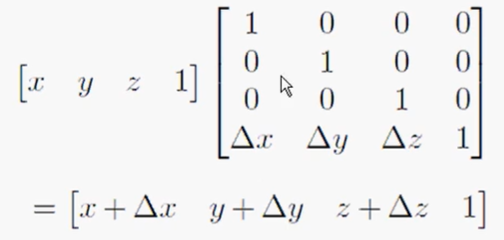
将线性变换和平移统一起来:

即得到一个新的矩阵M:

最后一行即为平移量。
没有平移的矩阵,即平移量为0:

参考资料&原文链接
Bilibili GAMES101-现代计算机图形学入门-闫令琪
本文标签
游戏开发、3D数学基础:图形与游戏开发、Unreal Engine、游戏开发基础、数学、游戏开发数学基础、书籍笔记。
标签:平移,矩阵,笔记,正交,行列式,余子式,向量,3D 来源: https://www.cnblogs.com/sin998/p/15229522.html