323. Number of Connected Components in an Undirected Graph 连通图的数量

You have a graph of n nodes. You are given an integer n and an array edges where edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.

Return the number of connected components in the graph.

Example 1:

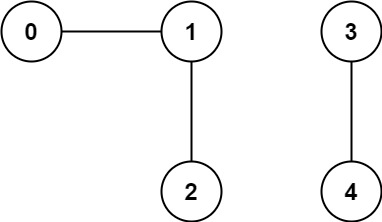
Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2

Example 2:

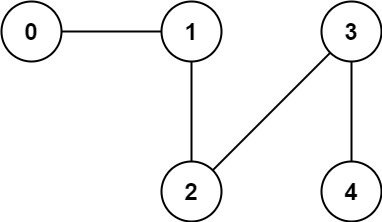
Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
Output: 1

dfs的思路是：无论递归栈多深，都只计算为1

class Solution {
    public int countComponents(int n, int[][] edges) {
        List<Integer>[] graph = new List[n];
        for (int i = 0; i < n; i++) graph[i] = new ArrayList<>();
        for (int[] e : edges) {
            graph[e[0]].add(e[1]);
            graph[e[1]].add(e[0]);
        }
        int components = 0;
        boolean[] visited = new boolean[n];
        for (int v = 0; v < n; v++) components += dfs(v, graph, visited);
        return components;
    }
    int dfs(int u, List<Integer>[] graph, boolean[] visited) {
        if (visited[u]) return 0;
        visited[u] = true;
        for (int v : graph[u]) dfs(v, graph, visited);
        return 1;
    }
}

标签：int,Graph,Number,boolean,323,edges,components,graph,visited
来源： https://www.cnblogs.com/immiao0319/p/15195894.html