PAT (Advanced Level) Practice 1146 Topological Order (25 分) 凌宸1642
作者:互联网
PAT (Advanced Level) Practice 1146 Topological Order (25 分) 凌宸1642
题目描述:
This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.
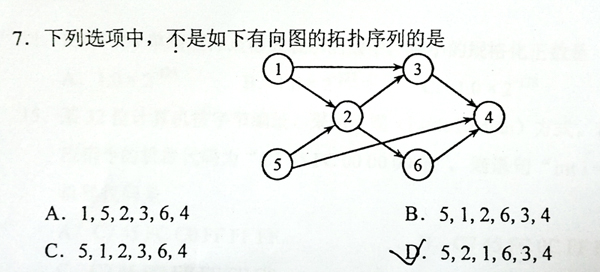
译:这是在2018年研究生入学考试中的一个考题:下列序列中哪一个不是给定有向图的拓扑序列?现在你应该编写一个程序来测试每一个选项。
Input Specification (输入说明):
Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.
译:每个输入文件包含一个测试用例。 对于每种情况,第一行给出 2 个正整数:图中顶点个数 N (≤ 1,000) 和 图中有向边的条数 M(≤ 10,000)。接下来 M 行,每行给出一条有向边的起点和终点。顶点编号从 1 到 N 。图的数据输入完后,接下来是另外一个正整数 K (≤ 100)。接下来 K 行查询,每行给出一个所有顶点的排列。所有在一行中的数字用一个空格隔开
output Specification (输出说明):
Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.
译:在一行中打印所有不是一个拓扑序列的查询的索引值。索引值从 0 开始。所有的数字必须用空格隔开,并且行首行末没有多余的空格。题目保证至少存在一个解。
Sample Input (样例输入):
6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
6
5 2 3 6 4 1
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6
Sample Output (样例输出):
0 4 5
The Idea:
-
首先得了解什么是拓扑排序
-
然后其实只要根据序列来判断,如果当前点入度为 0 ,则至少到目前是正确的,然后按照拓扑序列的规则,将其为起点的边划去(直接到达的终点的入度减一) 相反,如果此顶点的入度不为 0,却出现在序列中,则一定不是拓扑序列。
-
然后由于对于每次查询,图的数据是不会变的,但是存储顶点的入度数组的数据是会发生变化的,所以每次参与判断序列是不是拓扑序列的只能是图的入度数组的副本,这里使用了
transform()函数,也可以用vector存储,然后利用其assign函数也是可以做到的。
The Codes:
#include<bits/stdc++.h>
using namespace std ;
const int maxn = 1010 ;
vector<int> g[maxn] , ans;
int n , m , k , a , b ;
int indegree[maxn] = {0} , temp[maxn] , in2[maxn] ;
bool isTopologicalOrder(int in[] , int order[]){
int t ;
for(int i = 1 ; i <= n ; i ++){
t = order[i] ;
if(in[t] != 0) return false ; // 如果此时序列中的顶点的入度不为 0 则一定不是拓扑序列,直接返回 false
for(int j = 0 ; j < g[t].size() ; j ++)in[g[t][j]] -- ; // 如果此时顶点入度为 0 ,则该点所有能直接到达的顶点的入度 减一
}
return true ;
}
int op(int a){ return a ; }
int main(){
scanf("%d%d" , &n , &m) ;
for(int i = 0 ; i < m ; i ++){
scanf("%d%d" , &a , &b) ;
g[a].push_back(b) ;
indegree[b] ++ ;
}
scanf("%d" , &k) ;
for(int i = 0 ; i < k ; i ++){
for(int j = 1 ; j <= n ; j ++) scanf("%d" , &temp[j]) ;
transform(indegree + 1 , indegree + n + 1 , in2 + 1 , op) ; // 将 indegree 数组内 [1 , n] 的内容复制到 in2 的 [1 , n] 中
if(!isTopologicalOrder(in2 , temp)) ans.push_back(i) ;
}
for(int i = 0 ; i < ans.size() ; i ++) printf("%d%c", ans[i] , ((i == ans.size() -1)?'\n':' ')) ;
return 0 ;
}
标签:25,1146,Level,int,拓扑,000,maxn,each,序列 来源: https://www.cnblogs.com/lingchen1642/p/15164743.html