《量子计算与量子信息》2.1线性代数Linear algebra概述

量子力学对已知世界的描述是最精确和完整的，也是理解量子计算与量子信息的基础。

线性代数研究向量空间及其上的线性算子，牢固掌握初等线性代数是理解 好量子力学的基础。量子力学其实很容易学习，难学的印象来自某些应用中的困难。预备知识是初等线性代数，如果具备这方面的背景，读者就可以花一些时间做出那些简单的练习。

认同量子力学假设的主要障碍不在假设本身，而是为理解这些假设所需要 的大量线性代数概念，再加上物理学家在量子力学中所采用的不常见的Dirac 符号，这看起来（其实不然）相当可怕。

如表2 - 1所示是一些线性代数概念在量子力学中的标准记号，这种风格的记号称为Dirac记号。

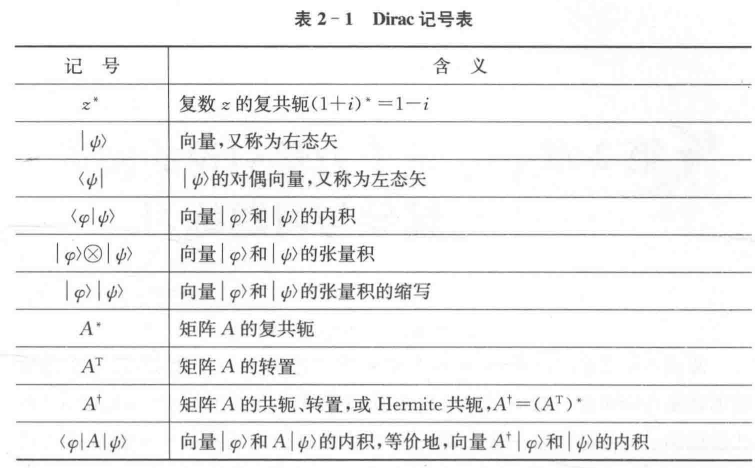
线性代数研究的基本对象是向量空间（vector space）,我们最感兴趣的向量空间是所有n元复数构成的向量空间，向量空间的元素称为向量， 有时也用列矩阵记号表示：

向量空间中列向量的标准量子力学符号为：

向量空间包含一个特殊的零向量，记作0。它满足性质：对任意向量，等式都成立。注意我们不用右态矢的记号表示零向量，这是唯一的 例外，原因是已有其他的含义

上向量的加运算的定义为

标量乘运算定义为

向量空间V的一个向量子空间是V的一个子集W,满足:W也构成一个向 量空间，即W必须对标量乘法和加法运算封闭。

标签：记号,Linear,量子力学,algebra,线性代数,空间,向量,量子
来源： https://www.cnblogs.com/yuxiaohan1236/p/15127727.html