长脖子鹿放置

题目背景

众周所知，在西洋棋中，我们有城堡、骑士、皇后、主教和长脖子鹿。

题目描述

如图所示，西洋棋的“长脖子鹿”，类似于中国象棋的马，但按照“目”字攻击，且没有中国象棋“别马腿”的规则。（因为长脖子鹿没有马腿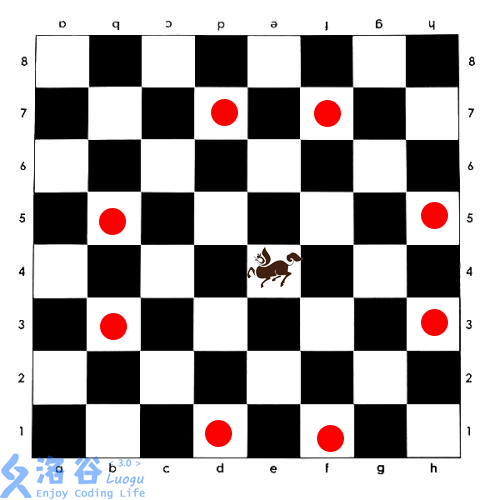）  给定一个$N * M$,的棋盘，有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。

输入输出格式

输入格式

 

输入的第一行为两个正整数$N$，$M$，$K$。其中$K$表示禁止放置长脖子鹿的格子数。 第$2$~第$K+1$行每一行为两个整数$X_i, Y_i$,表示禁止放置的格子。 不保证禁止放置的格子互不相同。

输出格式

 

一行一个正整数，表示最多能放置的长脖子鹿个数。

输入输出样例

输入样例 #1

2 2 1
1 1

输出样例 #1

3

输入样例 #2

/*额外提供一组数据*/
8 7 5
1 1
5 4
2 3
4 7
8 3

输出样例 #2

28

说明

**重要提示：请务必思考对图的遍历顺序对运行速度的影响** 对于$10$%的数据， $1 ≤ N,M ≤ 5$ 对于$30$%的数据， $1 ≤ N,M ≤ 10$ 对于$60$%的数据， $1 ≤ N,M ≤ 50$ 对于$80$%的数据， $1 ≤ N,M ≤ 100$ 对于$100$%的数据，$1 ≤ N,M ≤ 200$ 数据已修正，有一些错误的算法（包括部分题解）将不能通过本题。 感谢@Alpha 指出问题  

 1 #include <cstdio>
 2 #include <algorithm>
 3 #include <cstring>
 4 
 5 using namespace std;
 6 const int N = 500;
 7 int n, m , k;
 8 int g[N][N];
 9 #define PII pair <int, int>
10 PII match[N][N];
11 int vis[N][N], now;
12 
13 int dx[8] = {-1, -3, -3 ,-1 ,1 ,3, 3, 1};
14 int dy[8] = {3 ,  1, -1, -3, -3, -1 ,1, 3};
15 
16 bool find(int x,int y)
17 {
18     for(int i = 0 ; i < 8 ;i++)
19     {
20         int a = x + dx[i], b =y + dy[i];
21         if(a < 1 || a > n || b < 1 || b > m) continue;
22         if(g[a][b]) continue;
23         if(vis[a][b] != now)
24         {
25             vis[a][b] = now;
26             PII t = match[a][b];
27             if(t.first == 0 || find(t.first , t.second))
28             {
29                 match[a][b] = make_pair(x , y);
30                 return 1;
31             }
32         }
33     }
34     return 0;
35 }
36 
37 int main()
38 {
39     scanf("%d %d %d",&n,&m,&k);
40     int cnt = 0;
41     for(int i = 1; i <= k; i++)
42     {
43         int a, b;
44         scanf("%d %d",&a,&b);
45         if(g[a][b]) continue;
46         g[a][b] = 1;
47         cnt++;
48     }
49     int res = 0;
50     for(int i = 1; i <= n; i++)
51     {
52         for(int j = 1; j <= m; j++)
53         {
54             ++now;
55             if(i % 2 == 1 || g[i][j]) continue;
56             if(find(i, j)) res++;
57         }
58     }
59 
60     printf("%d", n * m - cnt - res);
61     return 0;
62 
63 }

 

   

标签：格子,int,样例,脖子,放置,include,P5030
来源： https://www.cnblogs.com/lyc-lb-blogs/p/14992593.html