P6855「EZEC-4.5」走方格 TJ
作者:互联网
这是一篇还布吉岛通没通过的题解~
前言
正解:动态规划
挺 duliu 一道题,难度较大 qwq。
PS:因为此篇题解前后改动较多,如果有什么错误请各位奆佬提出,本蒟蒻感激不尽 awa。
题意简述
给你一个 \(n\times m\) 大小的方格阵,可以把方格中的任意一个数改为 \(0\),每次从 \((1,1)\) 到 \((n,m)\) 的得分为路上所有数字的和。求每次改动数字后能得到的最大值的最小值。
法一:时间复杂度 \(Θ(m^2n^2)\) (TLE)
这但凡是个正常人都会想到吧……前两层循环枚举变为 \(0\) 的方格坐标,后两层按照正常的方格取数做法求最大值。
结果,被校 OJ 卡了没骗到分。
\(Code\)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int m,n,t,a[2005][2005];
ll ans=LONG_LONG_MAX,dp[2005][2005];
int main(){
scanf("%d %d",&m,&n);
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
scanf("%d",&a[i][j]);
}
}
for(int x=1;x<=m;x++){
for(int y=1;y<=n;y++){
memset(dp,0,sizeof(dp));
t=a[x][y];
a[x][y]=0;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
dp[i][j]=max(dp[i][j-1],dp[i-1][j])+a[i][j];
}
}
ans=min(ans,dp[m][n]);
a[x][y]=t;
}
}
printf("%lld",ans);
return 0;
}
法二:正解,时间复杂度 \(Θ(mn)\)
PS * 2:因为 me 习惯用 \(m\) 表示行 \(n\) 表示列,所以下列题解就会这么写。
有点麻烦。
如果每个点只能遍历一次,那么必须不变值和变为 \(0\) 这两种情况需要同时考虑。
首先我们可以考虑先求出从 \((1,1)\) 点出发走到 \((i,j)\) 点和从 \((m,n)\)出发走到 \((i,j)\) 点能拿到的最大分数,分别存在 \(dp1\) 数组和 \(dp2\) 数组里。
这两个数组很好求,按照每个初学 DP 者都要打的取数板子就珂以了。至于为什么要求这两个数组,我先卖个关子,待会儿就知道了(逃。
我们知道,如果你从 \((1,1)\) 出发,在走的时候不经过某个坐标为 \((i,j)\) 的点(也就是绕过这个点),你有两种情况可以绕开它:
-
从左边绕。
-
从上边绕。
给这两种方法更严谨的定义 \((i>0)\) :
-
从左边绕:经过点 \((x,y-i)\)。
-
从上边绕:经过点 \((x-i,y)\)。
对于这两种情况,我们可以分别用两个二维数组 \(l\) (左边绕)和 \(d\) (上边绕)来存:
-
\(l_{i,j}\) 表示从左边绕过 \((i,j)\) 点能获得的最大值。
-
\(d_{i,j}\) 表示从上边绕过 \((i,j)\) 点能获得的最大值。
但是如何求这两个数组呢?
直接切入可能比较麻烦。这个时候我们可以先分析这种情况:
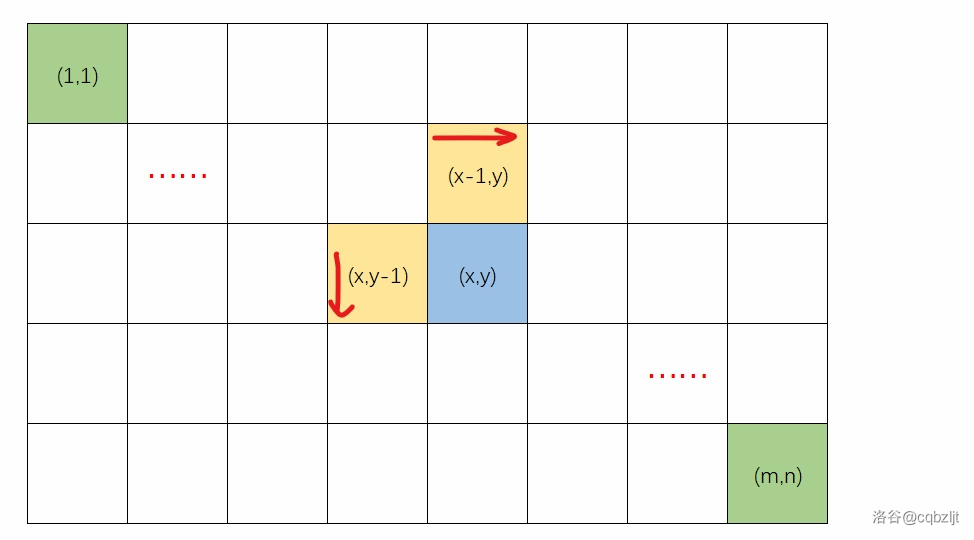
不管是往哪边绕,也不管前面怎么走,都紧贴着点 \((i,j)\) 过路方便分析,即,从左绕一定经过点 \((i,j-1)\),从上绕一定经过点 \((i-1,j)\)。
首先分析从左边绕的情况。
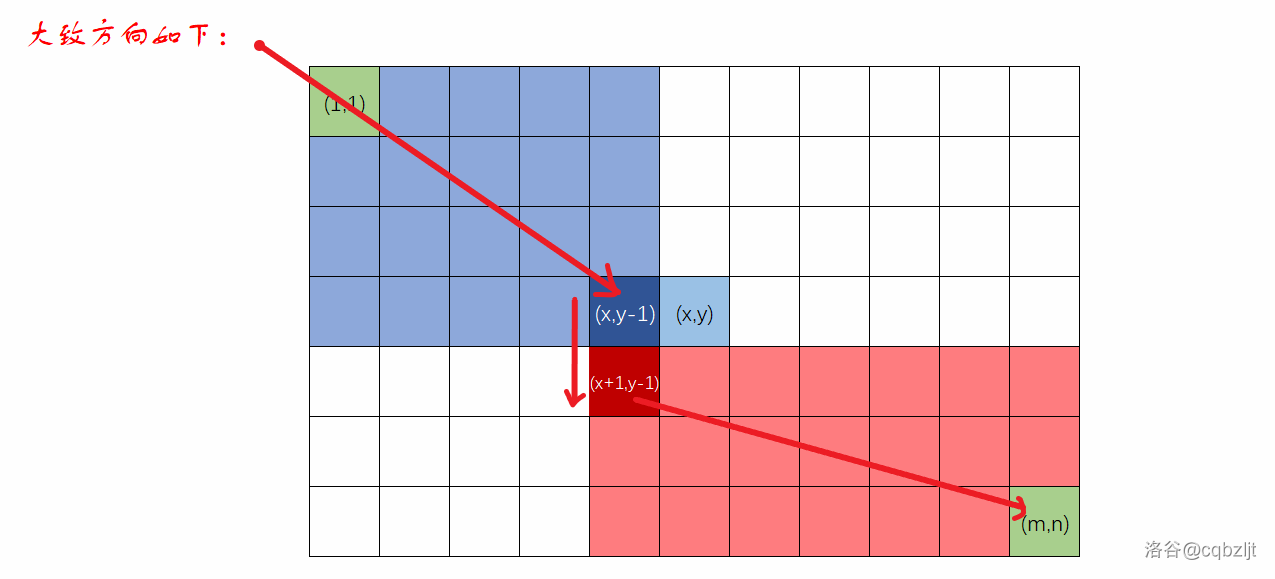
看图,蓝色区域表示从 \((1,1)\) 出发到点 \((i,j-1)\) 有可能会经过的区域,红色区域表示从点 \((i+1,j-1)\) 到 \((m,n)\) 有可能会经过的区域。至于为什么选这两个点呢,相信大家看图也能明白,因为选择这两个点可以做到经过的格子不重不漏,考虑到每种情况。
如果这么算,那么从点 \((i,j-1)\) 绕过去能拿到的最大分数就是:
\[score=dp1_{i,j-1}+dp2_{i+1,j-1} \]现在大家知道两个 \(dp\) 数组的意义了吧,就是用来求某个区域的最大分数的。因为如果每次循环到一个点就计算此点到终点的分数还需要两层循环会超时,基于走方格的方向是可逆的,我们只需要计算终点到每个点的最大分数就可以啦 OvO。
那我们现在只求了最贴近点 \((i,j)\) 的绕法,那我们如何求出往左绕的所有情况的最大值呢?
我们之前不是用了一个数组来存往左边绕的值吗?因为循环的顺序是从上到下,从左到右的,所以在求点 \((i,j)\) 的值时,我们已经把它左上方的所有值都求出来了。现在我们可以利用这些值,每一次,我们求当前 \(score\) 与之前最大分数的较大值,那每次都求最大值就是所有情况中的最大值。
那么最后的结果就是:
\[l_{i,j}=\max(dp1_{i,j-1}+dp2_{i+1,j-1},i_{i,j-1}) \]至于为什么我们利用的是 \(l_{i,j-1}\),大家可以自己画图感知,这个格子就位于我们前面求的必须经过的那个格子 \((i,j-1)\),那么绕过它我们就会求必须经过点 \((i,j-2)\),这样我们就又需要考虑绕过这个格子的情况,就又必须经过点 \((i,j-3)\)……这么一层一层往左推,最后可以推到点 \((i,1)\),从而把每种情况都考虑到。
从上面绕分析方法也差不多,这里不多说画张图让读者感知一下。
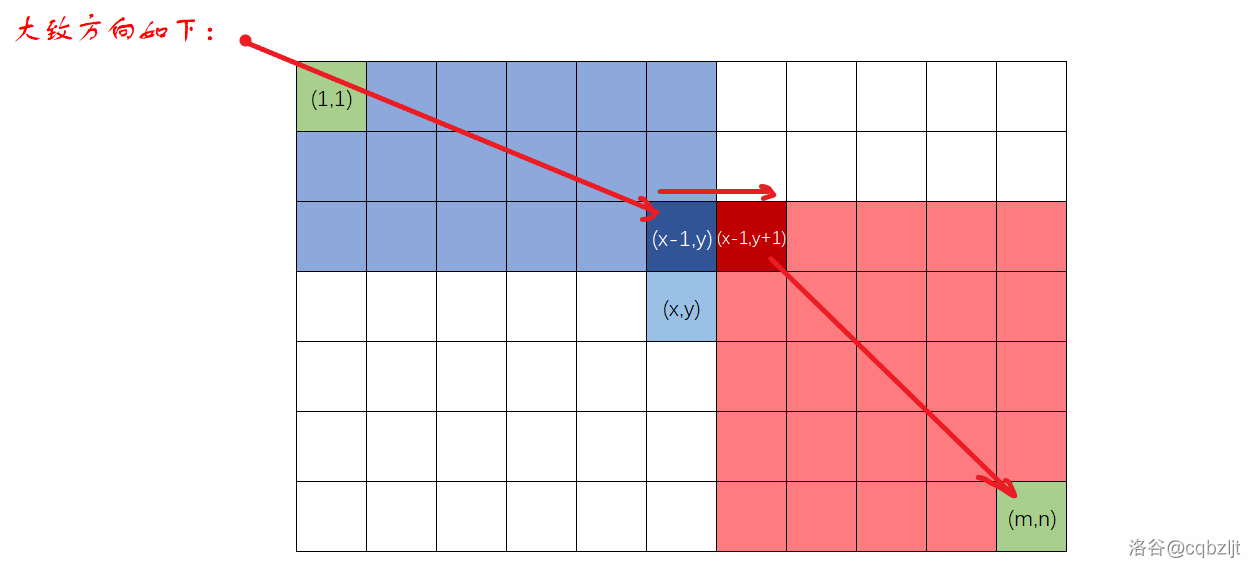
(您看看这两张图多像,连大小都差不多26 KB)
最后求出 \(d_{i,j}\) 的式子为:
\[d_{i,j}=\max(dp1_{i-1,j}+dp2_{i-1,j+1},d_{i-1,j}) \]最后求答案有些麻烦,因为题目要求的是变化后最能获得的最大分数的最小值,所以 \(\max\) 和 \(\min\) 是真的挺容易用混的,这里需要特别注意。
首先每对一个格子进行操作,最后得到的答案会是下列三种情况中的一种:
-
从左边绕过去得到的最大分数。
-
从上边绕过去得到的最大分数。
-
经过这个格子得到的最大分数。
前两个我们已经求解了,但其实第三种情况是灰常简单的!因为要保证经过点 \((i,j)\),所以我们只需要求 \(dp1_{i,j}+dp2{i,j}\) 就可以了。但是上面那个式子算了两次 \((i,j)\) 的值,而我们因为把它变成 \(0\) 了,就一次都不能算。所以还需要减去两个 \(a_{i,j}\)。
所以最后的答案终于可能被更新了 owo:
\[ans=\min\big(ans,\max(l_{i,j},d_{i,j},dp1_{i,j}+dp2_{i,j}-2\times a_{i,j})\big) \]最后再强调一遍要注意最大值和最小值别用反了啊! 别问我为什么知道(悲)。
\(Code\)
#include<bits/stdc++.h>
#define ll long long //记得要开long long哦!
using namespace std;
//温馨提示细节:因为最后答案还是求的最小值,所以 ans 需要定义极大值
ll m,n,ans=LONG_LONG_MAX,a[2005][2005],dp1[2005][2005],dp2[2005][2005],l[2005][2005],d[2005][2005];
int main(){
//输入
scanf("%lld %lld",&m,&n);
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
scanf("%lld",&a[i][j]);
}
}
//求两个 dp 数组的值
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
dp1[i][j]=max(dp1[i-1][j],dp1[i][j-1])+a[i][j];
}
}
for(int i=m;i;i--){
for(int j=n;j;j--){
dp2[i][j]=max(dp2[i+1][j],dp2[i][j+1])+a[i][j];
}
}
//核心代码开始
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
l[i][j]=max(l[i][j-1],dp1[i][j-1]+dp2[i+1][j-1]);
d[i][j]=max(d[i-1][j],dp1[i-1][j]+dp2[i-1][j+1]);
ans=min(ans,max(max(l[i][j],d[i][j]),dp1[i][j]+dp2[i][j]-2*a[i][j]));
}
}
//核心代码结束,输出答案
printf("%lld",ans);
return 0;
}
写在最后
这真的是一道很好的动态规划题,很考验思维,也有很多需要注意的细节。最后,看在本人写了那么久的份上,就请您随手点一下左下角那个小小的赞吧 qwq。
标签:4.5,分数,dp2,dp1,最大值,long,P6855,TJ,2005 来源: https://www.cnblogs.com/cqbzljt0152/p/14872294.html