OO第三单元总结

架构分析

---

该单元中由于给出了jml规格，除相关自定义数据结构外基本为实现要求的每一个异常类与相关接口，没有特殊架构。

bug分析

第九次作业

本次作业由于实现并查集时，错误使用了hashmap，在连接两个节点时可能会导致与第二个节点连接的节点同第一个节点不连通，产生错误，强测炸了一半的点。

修复bug时重新实现了标准并查集。

第十次作业

由于在实现qgvs时，采用了两层遍历的方式，导致$O(V^2)$时间复杂度过大，互测中被hack

修复bug采用了改为遍历每一个人的acquaintance数组，降低复杂度为$O(E)$。

第十一次作业

此次作业没有被查出bug

度量分析

第九次作业

UML类图：

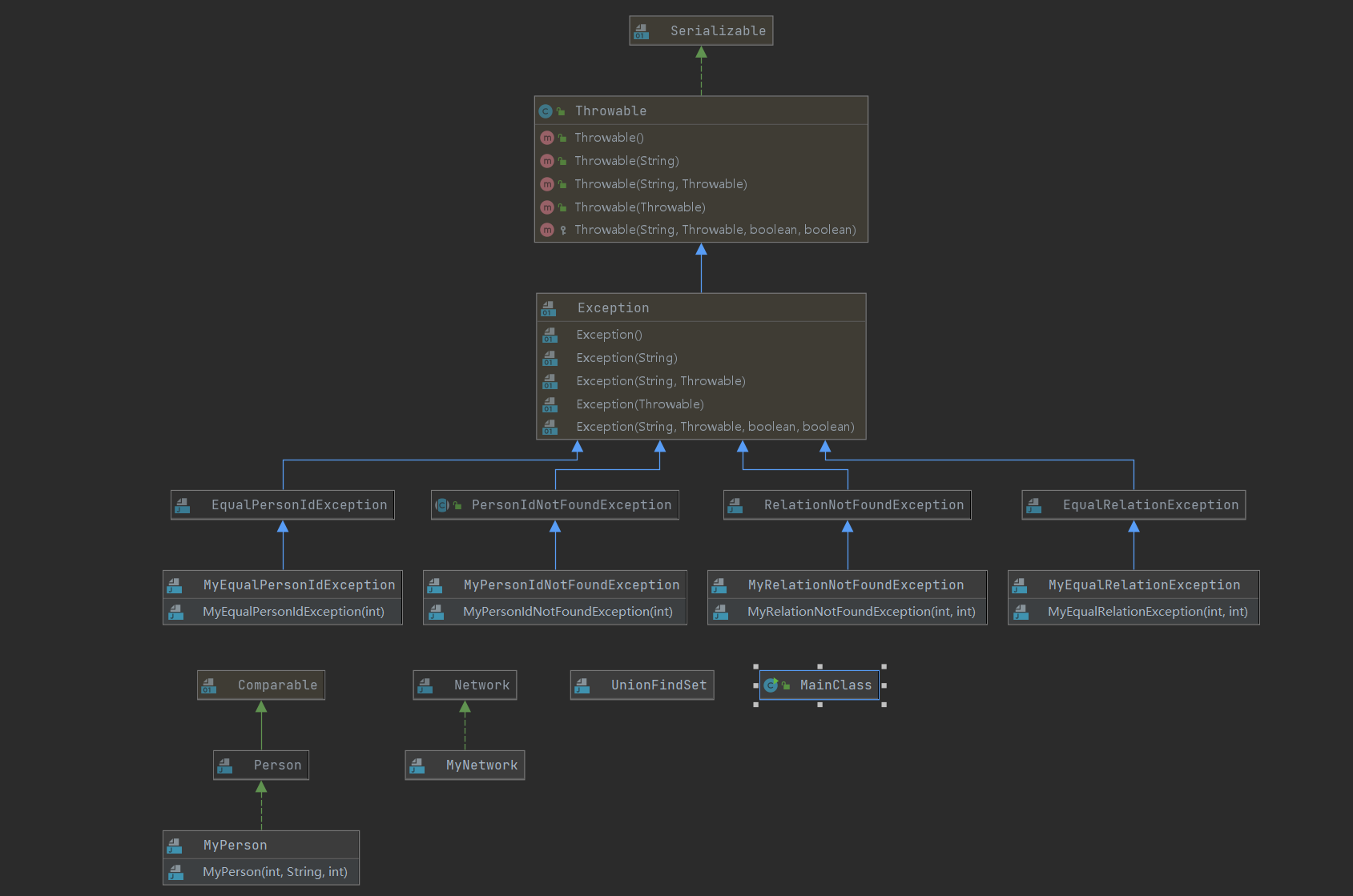
除并查集类之外，其余类均为直接继承给定异常类或实现相关接口。

度量分析：

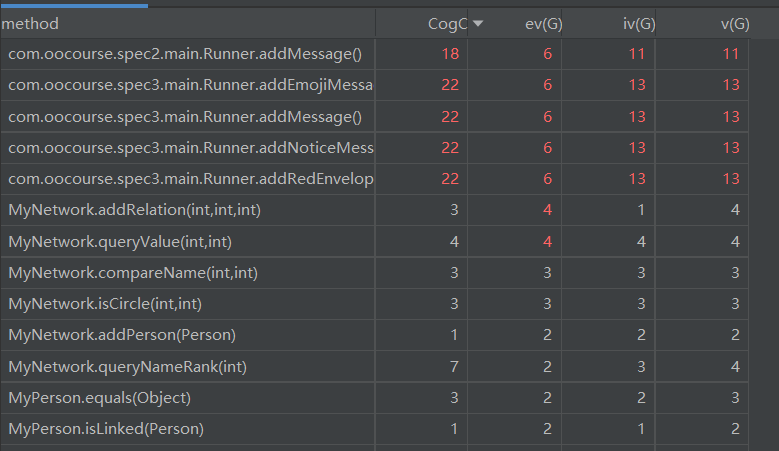
可以看出，复杂度较高的方法仅有MyNetwork.addRelation和MyNetwork.queryValue，这两者复杂度较高的原因为需要处理的异常较多。

第十次作业

UML类图：

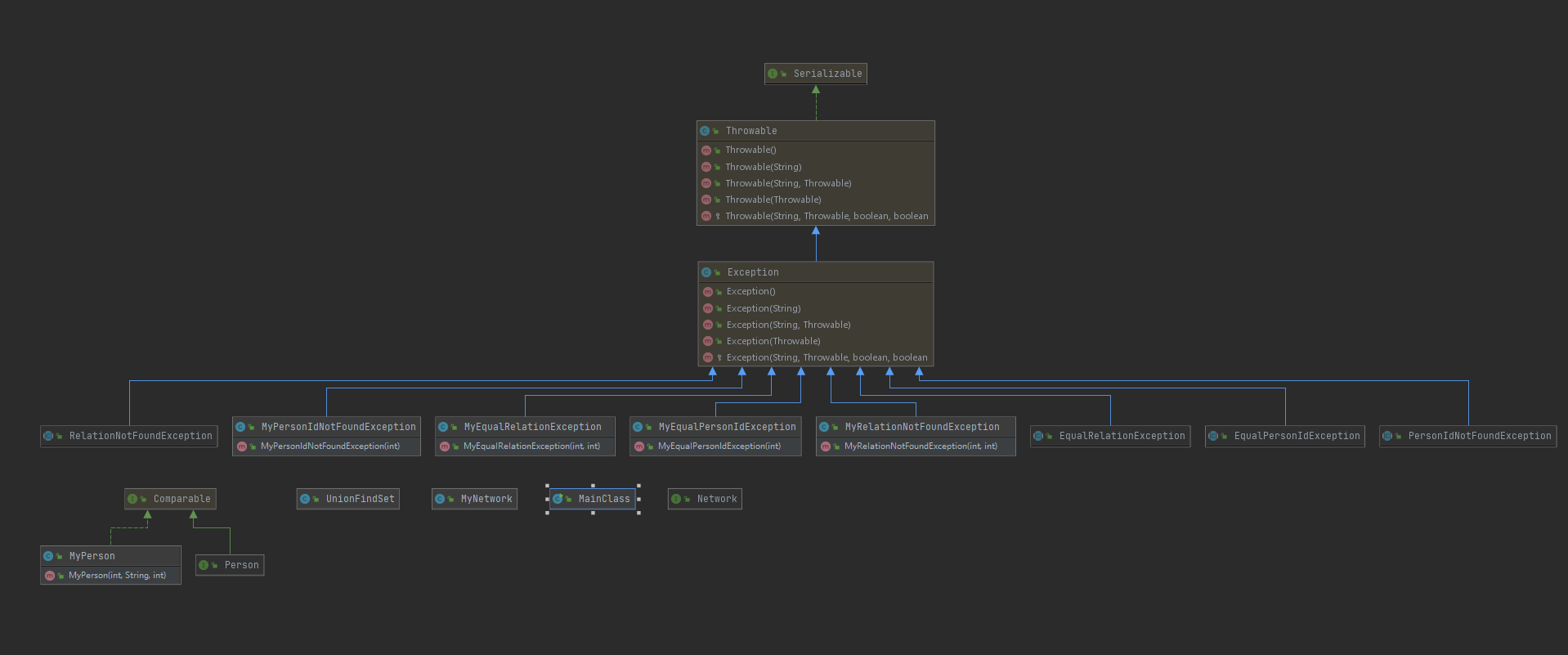
相比上一次增加的类均为实现相关异常类以及相关接口。

度量分析：

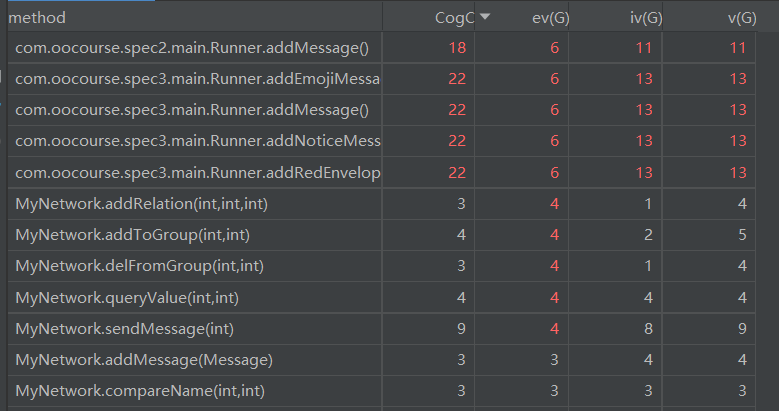
除了沿用上一次作业的MyNetwork.addRelation和MyNetwork.queryValue，此次作业中MyNetwork.delFromGroup，MyNetwork.addToGroup, MyNetwork.sendMessage的圈复杂度也较高，均由于处理异常导致分支增加。

第十一次作业

UML类图：

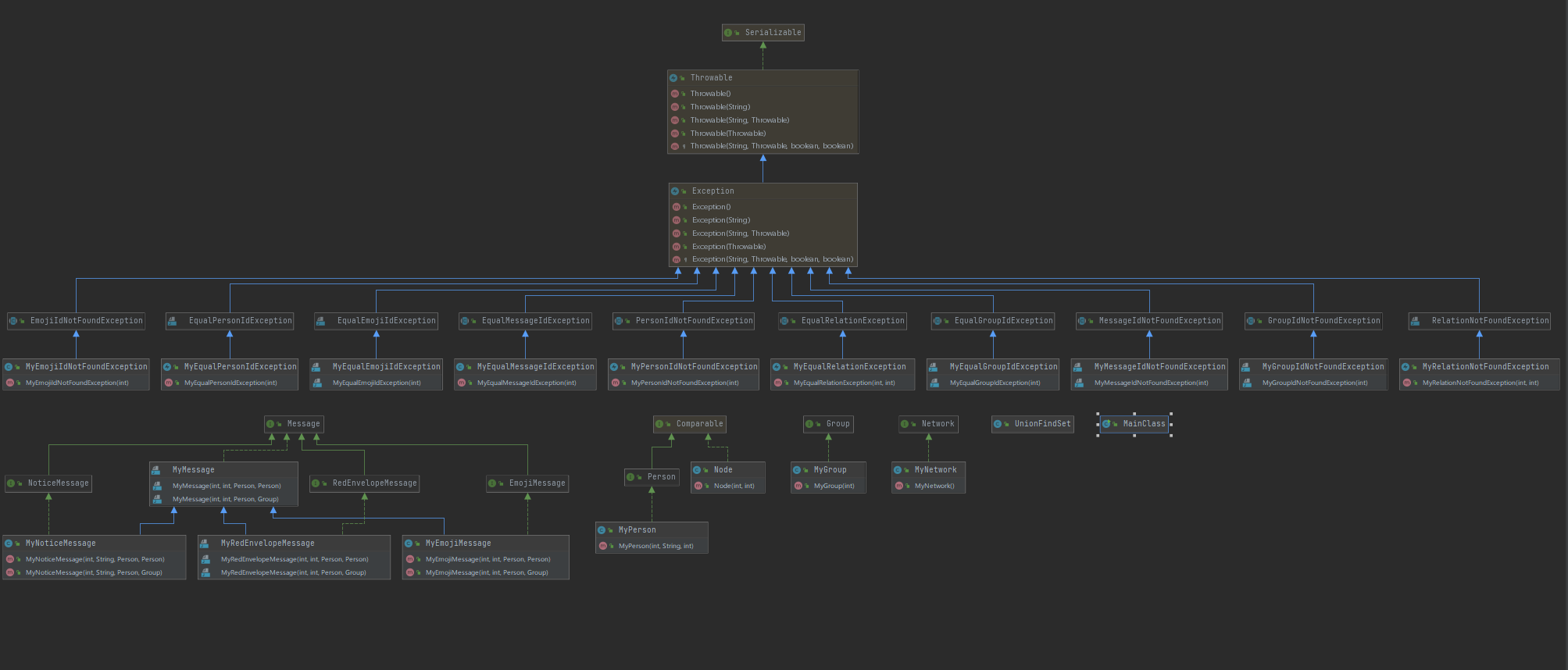
除相关的异常类与接口实现外，添加了Node作为迪杰斯特拉算法的辅助类

度量分析：

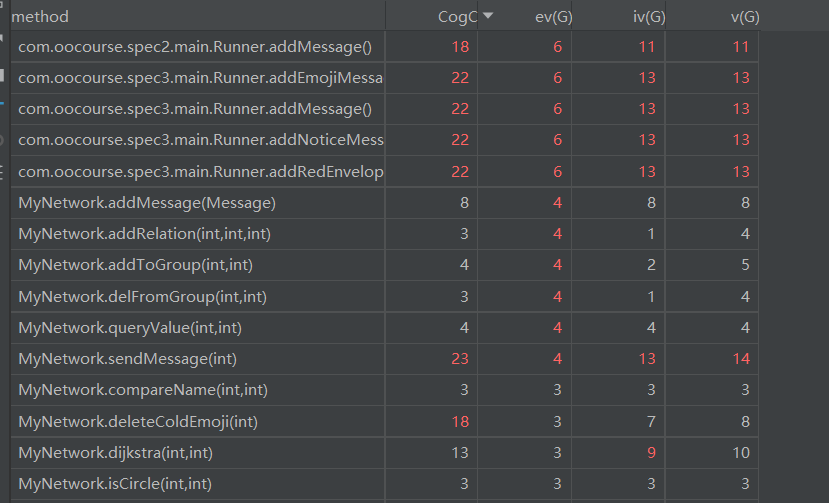
此次作业中复杂度较高的方法增加了不少。

因为在实现MyNetwork.sendMessage时，直接进行了RedEnvlopeMessage,EmojiMessage的分别处理与筛选，而且在type1与type0中分别实现了一遍，导致复杂度较高。可以考虑将处理特殊类型消息部分的代码抽象成一个方法，降低复杂度。

MyNetwork.deleteCodeEmoji方法中，为了降低时间复杂度，引入了新的数据结构用于加速查找，导致复杂度较高。详细见时间复杂度分析部分。

时间复杂度分析与容器类的选择

第九次作业

为加速根据id查找people，采用了Map容器建立id到people的映射。为了加速qnr考虑采用有序数据结构TreeMap，但由于TreeMap并未提供原生的由元素获得序号，并未进行相关加速部分的实现。

为了加速qci，采用了并查集加速查找。作业中实现的并查集有误，在bug修复中修改成标准并查集，递归实现路径压缩。

ap的复杂度均取决于TreeMap，为$O(log(n))$。由于并查集的特征，qci的复杂度优于$O(log(n))$。

为了加速qbs，在并查集中记录连通分量的个数，每插入一个元素将连通分量个数加一，每合并两个连通分量将连通分量个数减一，实现$O(1)$的查询。

为加速qv，在people中采用了HashMap将id映射到value，复杂度为$O(1)$，因此ar的复杂度也为$O(1)$

第十次作业

为加速依照id查找group与message，在network中采用HashMap实现从id到group、message的映射，插入、查找、删除复杂度均为$O(1)$。同理，group中也采用HashMap存储id与people。

本次作业中并未针对qgvs, qgam, qgav进行优化，qgam与qgav的复杂度为$O(V)$，qgvs的复杂度为$O(V^2)$。也因此在互测中qgvs超时。

通过更改遍历策略，仅遍历有联系的人而非遍历所有人再判断有无联系，将qgvs复杂度降为O(E)。

第十一次作业

本次作业中复杂度最高的操作为sim，用到了迪杰斯特拉算法。基础的算法的复杂度为$O(V^{2)$，在此次作业插入节点与查询均为1条指令很容易出现接近$5000}3$级别的运算，复杂度较高。而采用堆优化后，复杂度变为$O(Elog(E))$。插入节点与增加边均为1条指令，总运算级别一定低于$10000log(10000)$，因此采用了堆优化的迪杰斯特拉算法。

初次之外，对dci进行了优化。对于message，维护三个容器类，分别为由emojiId到对应message集合的HashMap，emojiId到其time的HashMap映射以及time到所有heat为time的emojiId集合的HasmMap。通过这样，在删除时直接可以$O(1)$查找到需要删除的消息。

测试策略

jml规格为单元测试提供了一定程度的便利，大多数行为都已经规定好，可以直接获得测试指标。

但到了层次较高的部分，类中的各个部分相互耦合，难以进行单元测试，可以通过黑盒测试来验证其正确性。

给定相同的指令序列，有且仅由一种正确输出，因此对拍机的实现较为容易。

标签：OO,总结,MyNetwork,实现,qgvs,复杂度,作业,id,单元
来源： https://www.cnblogs.com/kirimiko/p/14838640.html