机器学习中的数值查找算法(3)——哈希查找算法

原文链接：机器学习中的数值查找算法(3)——哈希查找算法 – 每天进步一点点 (longkui.site)

0.前言

前面介绍的查找算法均是基于有序序列的查找方式，哈希查找是通过计算元素的存储地址进行快速查找方式，它并不要求序列一定有序，可以通过如下四个步骤完成元素进行查找。

• 用哈希函数构造哈希表。
• 将元素进行哈希函数过滤，选择其存储的地址。
• 将需要查找的元素经过哈希函数映射到存储地址。
• 在存储地址中，查找函数是否存在。

1.详细说明

哈希函数和哈希表的结构是哈希查找中最重要的两个因素，直接影响了哈希的查找速度。哈希表（Hash Table， 亦称散列表），是依据Key-Value构建的数据结构，Key由哈希函数产生，用以加快查找速度。

哈希函数的构造方法有很多，比如直接地址法、平方取中法、除数留余法、随机数法、数字分析法及折叠法等。

• 直接地址法。直接地址法是一种线性的函数方法，可以利用公式f(key) =a*key+b 表示。其中，a、b为常变量，将key的值传递到函数中，直接生成在哈希表中的映射地址。
• 平方取中法。平方取中法是一种数值截取方法，将一个数值进行平方计算后取中间的若干值。例如，数值886的平方为784996，可以取中间四位数8499作为886的哈希值。
• 除数留余法。除数留余法是通过将数值对某值进行求余，可以用f(key)=key%p（p<=N）表示，其中，N为散列表的长度。例如数值为45687，对10000求余数5687，则5687可视为数值45687的哈希值。
• 随机数法。随机数法将数值作为随机种子传入随机函数，通过随机的方法得到相应的哈希值，用公式表示即f(key)=random(key)。
• 数字分析法。数字分析法是根据数组的特征进行分析。例如，某公司拥有众多员工，采用8位数字对员工进行编号，（如51-58-1396），前面两位是部门编号，中间两位是员工岗位类型，最后四位是员工编号，因此当在某个部门内时，只需最后四位代码替代员工编号即可。
• 折叠法。折叠法是将关键词按照一定的位数进行切分，将切分的若干部分进行数值相加，并根据散列表的长度，取末尾的几个数值作为哈希值。例如，将数值123456789切分成三部分，然后叠加相加，即123+456+789=1368，并将末尾的三位数作为哈希值。

虽然可以通过上述6种方法产生相应的哈希值，但是随着数据量的增加，当超越哈希表的长度时，就可能产生数值冲突。例如，在除数留余法中，45687对10000 求得的余数是5687，但是用同样的方法55687 对10000 求得的余数依然是5687，则45687与55687的哈希值冲突，当两者同时出现的时候会导致误判或者误查找。

通过良好的哈希函数，可以减少一些冲突，但是冲突是哈希函数中不可避免的问题。哈希冲突的解决方法有很多，如开放定址法，再哈希法，链地址法等，它们的共同特征是在发生冲突之后，通过其他的数据结构或者其他方式解决冲突。

以链地址法为例，它的核心思想是将所有哈希值冲突的元素组成一个单链表，并将单链表的头指针存入哈希表元素中。例如，一组数值{19，23，3，56，10，17，12，29}，哈希表的长度为5，哈希函数方法为除数留余法，则用链地址法处理冲突如下图所示：

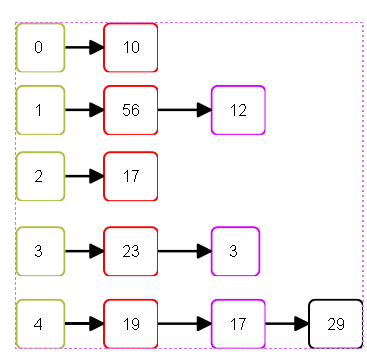
通过链地址法虽然解决了冲突，但是平均查找长度也有所增加。例如，在上图的例子中平均查找长度为（1+1+2+1+1+2+1+2+3）/ 8 =1.75

标签：key,函数,算法,数值,地址,查找,哈希
来源： https://www.cnblogs.com/longkui-site/p/16650057.html