elasticsearch算法之推荐系统的相似度算法(一)
作者:互联网
一、推荐系统简介
推荐系统主要基于对用户历史的行为数据分析处理,寻找得到用户可能感兴趣的内容,从而实现主动向用户推荐其可能感兴趣的内容;
从物品的长尾理论来看,推荐系统通过发掘用户的行为,找到用户的个性化需求,从而将长尾商品准确地推荐给需要它的用户,帮助用户发现那些他们感兴趣但很难发现的商品。
推荐系统使用的是基于邻域的算法,一类是基于用户的协同过滤算法,另一类是基于物品的协同过滤算法;
二、数据集准备
我们采用GroupLens提供的MovieLens数据集
These files contain 1,000,209 anonymous ratings of approximately 3,900 movies
made by 6,040 MovieLens users who joined MovieLens in 2000.
使用一下code加载评分文件ml-1m/ratings.dat
def get_ratings():
ratings = pd.read_csv('ml-1m/ratings.dat',
sep='::',
names=['UserID', 'MovieID', 'Rating', 'Timestamp'],
nrows=100000
)
return ratings
我们可以查看前五行的数据情况
rating = get_ratings()
print(rating.head())
UserID MovieID Rating Timestamp
0 1 1193 5 978300760
1 1 661 3 978302109
2 1 914 3 978301968
3 1 3408 4 978300275
4 1 2355 5 978824291
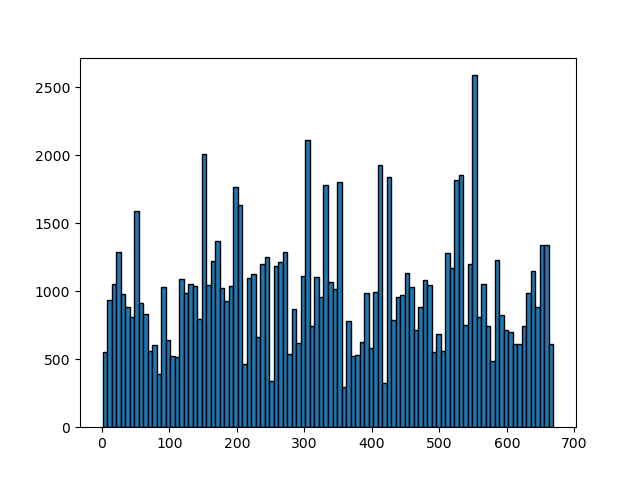
了解一下用户感兴趣的电影数量
rating = get_ratings()
plt.hist(rating['UserID'], bins=100, edgecolor='black')
plt.show()
三、基于用户的协同过滤算法
基于用户的协同过滤算法是推荐系统中最古老的算法,该算法首先需要找到跟当前用户兴趣相似的用户,然后将找到的用户感兴趣却不在当前用户兴趣列表的物品推荐给当前用户;
基于用户的协同过滤算法主要分为两步
- 找到和当前用户兴趣相似的用户集合;
该算法基于用户对物品的历史的正反馈行为计算用户兴趣相似度;我们给定用户u、v,令N(u)表示用户u曾经有过正反馈的物品集合,N(v)表示用户v曾经有过正反馈的物品集合;我们可以通过余弦相似度来计算用户u和v的相似度:
w_{uv} = \frac{N(u) \cap N(v)}{\sqrt {N(u) \cup N(v)}}
例如用户U对a、b、c有过正反馈记录,用户V对a、c有过正反馈记录;
U a b c
V a c
我们利用余弦相似度可以计算U和V的兴趣相似度
\[w_{UV}=\frac{|\{a,b,c\} \cap \{a,c\}|}{\sqrt {|\{a,b,c\}| |\{a,c\}|}} = \frac{2}{\sqrt{6}} \]我们使用如下的user_similarity来计算用户相似性
def user_similarity(ratings):
matrix = []
rating_groups = ratings.groupby('UserID')
for u_id, u_ratings in rating_groups:
row = []
matrix.append(row)
u_movieIds = u_ratings['MovieID'].values
for v_id, v_ratings in rating_groups:
v_movieIds = v_ratings['MovieID'].values
u_v_movieIds = np.intersect1d(u_movieIds, v_movieIds)
similarity = len(u_v_movieIds)/math.sqrt(len(u_movieIds) * len(v_movieIds))
row.append(similarity)
result = pd.DataFrame(matrix, columns= rating_groups.groups.keys(), index=rating_groups.groups.keys())
return result
rating = get_ratings()
similarity_matrix = user_similarity(rating)
print(similarity_matrix.head(10))
1 2 3 ... 667 668 669
1 1.000000 0.084657 0.115406 ... 0.010504 0.068680 0.076194
2 0.084657 1.000000 0.147945 ... 0.087529 0.161416 0.048839
3 0.115406 0.147945 1.000000 ... 0.085666 0.070014 0.077674
4 0.119898 0.153704 0.152783 ... 0.083438 0.036370 0.000000
5 0.097618 0.125142 0.059708 ... 0.119562 0.142134 0.059131
6 0.163017 0.114939 0.099710 ... 0.063529 0.000000 0.032915
7 0.049341 0.284641 0.150899 ... 0.164817 0.179605 0.099627
8 0.116508 0.201633 0.083139 ... 0.090808 0.113092 0.023525
9 0.200125 0.162482 0.122407 ... 0.118842 0.178069 0.053877
10 0.240081 0.215441 0.216773 ... 0.126021 0.083229 0.096951
[10 rows x 669 columns]
在以上代码中直接遍历所有的用户进行计算相似性,很多时候由于物品的数量比较多或者每个用户的兴趣关注点比较少,这会导致大量用户并不存在所谓的并集;我们可以先将数据结构反转为产品用户,然后计算不同用户感兴趣的产品总数和相关用户之间感兴趣的产品交集,最后再进行余弦相似性计算;
import math
import numpy as np
import pandas as pd
def change_user_ratings(rating):
grouped = rating.groupby('MovieID')
result = {}
for movieId,m_rating in grouped:
result[movieId] = m_rating['UserID'].values
df = pd.DataFrame({
'MovieID': result.keys(),
'UserIDs': result.values()
})
return df.set_index(df.columns.values[0])
def cal_count(product_users):
user_counts = {}
rel_user_counts = {}
for movieId, row in product_users.iterrows():
userIds = row['UserIDs']
for uid in userIds:
if uid not in user_counts:
user_counts[uid] = 0
user_counts[uid] += 1
for vid in userIds:
if (uid, vid) not in rel_user_counts:
rel_user_counts[(uid, vid)] = 0
rel_user_counts[(uid, vid)] += 1
user_counts = pd.DataFrame({'UserID': user_counts.keys(), 'Movie_Count': user_counts.values()})
rel_user_counts = pd.DataFrame({'Rel_UserID':rel_user_counts.keys(), 'Movie_Count':rel_user_counts.values()})
return user_counts.set_index(user_counts.columns.values[0]), rel_user_counts.set_index(rel_user_counts.columns.values[0])
def cosin_similarity(user_counts, rel_user_counts):
result = []
for u, u_row in user_counts.iterrows():
row = []
result.append(row)
u_count = u_row['Movie_Count']
for v, v_row in user_counts.iterrows():
v_count = v_row['Movie_Count']
if rel_user_counts.index.isin([(u,v)]).any():
count = rel_user_counts.at[(u,v), 'Movie_Count']
row.append(count/math.sqrt(u_count * v_count))
else:
row.append(0)
return pd.DataFrame(result, index=user_counts.index.values, columns=user_counts.index.values)
def user_similarity(ratings):
rating_users = change_user_ratings(ratings)
user_counts, rel_user_counts = cal_count(rating_users)
s = cosin_similarity(user_counts, rel_user_counts)
return s
ratings = get_ratings()
similarity_matrix = user_similarity(ratings)
print(similarity_matrix.head(10))
1 2 3 ... 667 668 669
1 1.000000 0.084657 0.115406 ... 0.010504 0.068680 0.076194
2 0.084657 1.000000 0.147945 ... 0.087529 0.161416 0.048839
3 0.115406 0.147945 1.000000 ... 0.085666 0.070014 0.077674
4 0.119898 0.153704 0.152783 ... 0.083438 0.036370 0.000000
5 0.097618 0.125142 0.059708 ... 0.119562 0.142134 0.059131
6 0.163017 0.114939 0.099710 ... 0.063529 0.000000 0.032915
7 0.049341 0.284641 0.150899 ... 0.164817 0.179605 0.099627
8 0.116508 0.201633 0.083139 ... 0.090808 0.113092 0.023525
9 0.200125 0.162482 0.122407 ... 0.118842 0.178069 0.053877
10 0.240081 0.215441 0.216773 ... 0.126021 0.083229 0.096951
[10 rows x 669 columns]
- 找到这个用户集合感兴趣的且当前用户没有听说过的物品推推荐给他;
通过以上计算我们得到了用户相似性的矩阵,接下来我们需要找到跟目标用户兴趣最相似的K个用户,然后将只有这K个用户喜欢的物品推荐给目标用户;这里我们需要进一步度量目标用户对特定产品的感兴趣程度
在这个公式中,S(u,K)包含和用户u兴趣最接近的K个用户,N(i)是对物品i有过行为的用户集合,Wuv 是用户u和用户v的兴趣相似度,rvi 代表用户v对物品i的兴趣,这里使用评分除以5来计算。
\[p(u,i) = \sum_{v \in s(u,K) \cap N(i)} w_{uv} r_{vi} \]我们使用以下的recommend方法实现这个推荐
def recommend(ratings,u, matrix, k):
result = pd.Series(dtype='float64');
grouped = dict(list(ratings.groupby('UserID')))
u_ratings = grouped[u][['MovieID','Rating']]
row = matrix.loc[u].sort_values(ascending=False)
for v in row.index:
if u != v:
similarity = row.loc[v]
v_ratings = grouped[v][['MovieID','Rating']]
diff = pd.concat([v_ratings, u_ratings, u_ratings]).drop_duplicates(subset=pd.Index(['MovieID']), keep=False)
for movieId, s_rating in diff.set_index('MovieID').iterrows():
like = similarity * (s_rating['Rating']/5)
s_movieId = str(movieId)
if movieId in result:
result[s_movieId] += like
else:
result[s_movieId] = like
return result.sort_values(ascending=False).head(k)
我们计算推荐给用户A且其最感兴趣的前三件商品;从计算结果可以看到是商品c和e;
ratings = get_ratings()
similarity_matrix = user_similarity(ratings)
recommend_movies = recommend(ratings, 1, similarity_matrix, 10)
print(recommend_movies.head(10))
2049 0.240081
3292 0.212965
1067 0.204131
2559 0.193922
3620 0.168068
963 0.168068
2179 0.165928
2211 0.165928
1817 0.165928
2227 0.165928
dtype: float64
注:由于rating.data的数据实际情况,每个用户以及每个电影都会有对应的评分,所以第二种算法并不具有什么性能优势,需要根据自己数据的实际情况进行选择;
标签:ratings,rating,...,用户,算法,elasticsearch,user,相似,counts 来源: https://www.cnblogs.com/wufengtinghai/p/15848684.html