神秘构造题
作者:互联网
Coloring Torus AGC030C:https://www.luogu.com.cn/problem/AT4512
考虑如果 \(k\le n\),那么直接一行一种颜色就行了
如果 \(k>n\),考虑可以转化为在对角线上染色,由于这个相邻的定义是循环的,所以合法:
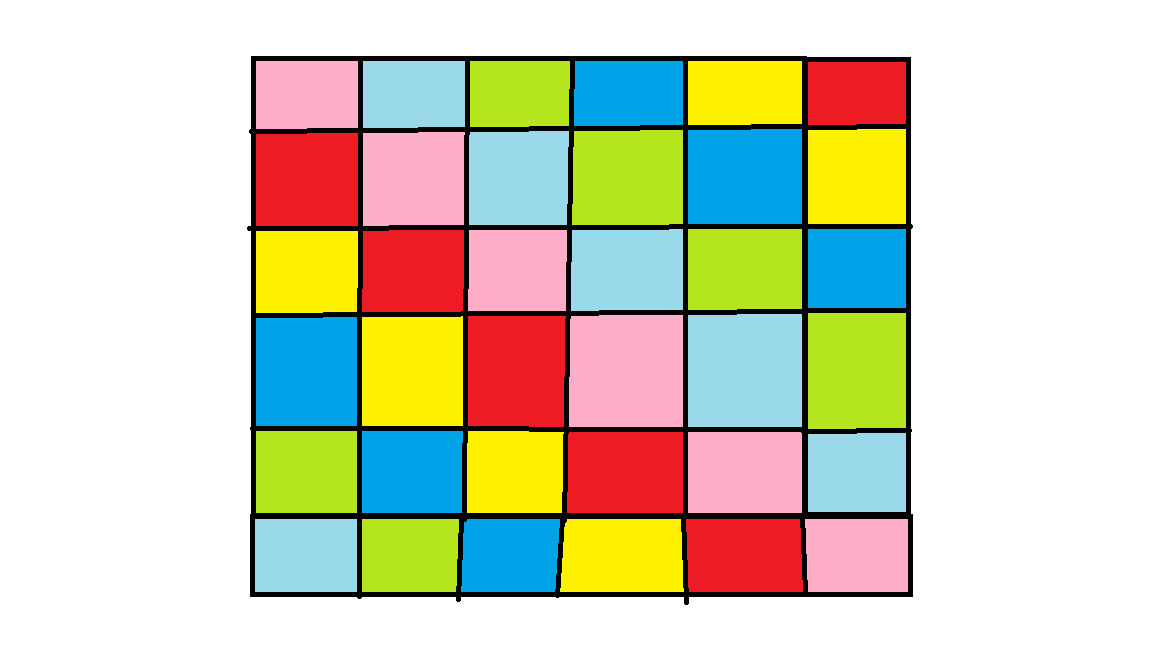
但这样仍然只能构造最多 \(n\) 中颜色,但发现可以把一部分对角线交替染色:

于是就可以了
Modulo Matrix AGC027D:https://www.luogu.com.cn/problem/AT4378
一个想法是先把格子黑板染色来分类,然后白点取它相邻的四个黑点的 \(\operatorname{lcm}+1\)
但这样如果在黑点上乱填的话值域仍然会炸
所以考虑对每一条穿过黑点的对角线(两个方向都算)确定一个质数,一个黑点的值就填两条穿过它的对角线的质数的乘积
然后就是如何确定这些质数的位置
先考虑所有从左上到右下的对角线,质数从小到大隔一条放一个,然后考虑从左上到右下的对角线,仍然是从小到大隔一条放一个
然后在重新考虑左上到右下的对角线,把那些没放的条再从小到大放上,左上到右下的也是同理
这样搞出来的有什么特点?就是由于质数是一个大一个小来放置的,所以同一个白点四周的四个黑点不会同时太大,也就不会乘炸了
Choosing Points AGC025D:https://www.luogu.com.cn/problem/AT3967
一个结论是平面上距离为 \(\sqrt{r}\) 的整点构成二分图
按照 \(r \bmod 4\) 分类,考虑 \(a^2+b^2=r\)(分别是横纵坐标的差值)
- \(r\equiv 3\pmod 4\),没有符号要求的 \(a,b\)
- \(r\equiv 1\pmod 4\),\(a,b\) 奇偶性不同,那么按棋盘的方式黑白染色
- \(r\equiv 2\pmod 4\),\(a,b\) 都是奇数,隔行染色
- \(r\equiv 0\pmod 4\),把 \(a,b\) 都缩小一半转化为上面的情况
于是在 \(\sqrt{D1}\) 的分类关系下能取出大小大于等于全集一半点
然后在这一些点中再按照 \(\sqrt{D2}\) 的分类关系取出大小大于等于全集四分之一的点
CF1270E Divide Points
标签:神秘,黑点,质数,构造,pmod,对角线,左上,equiv 来源: https://www.cnblogs.com/suxxsfe/p/14748799.html