机器人运动逆解算IK

文章目录

• • Inverse kinematics
  • • 基本概念
    • 范例
  • 数学推导
  • • DH模型
    • • 坐标系定义
      • 参数定义
      • 坐标变换
    • Jacobian矩阵
  • CoppeliaSim
  • • 内置模块
    • • 范例
      • 构建IK组
    • 外部编程

Inverse kinematics

基本概念

从任务(task)空间坐标到关节(joints)空间坐标的转换。

IK element元素：由基点base、连杆links、关节joints、顶点tip、靶target组成，如上图所示

IK group组：整体，包含至少一个IK元素，在IK组基础上定义properties；复杂情况下多个IK元素有共同关节，需要同时进行求解，必须放在相同IK组中并确定次序（如下图所示）

IK element的目标：使得Tip与Target重合并有一定约束

注意：需要确定运动学链的properties的正确性

当IK元素过度约束时，采用damped resolution method(e.g.DLS)，迭代最小化tip和target的距离，并约束使tip朝向target

范例

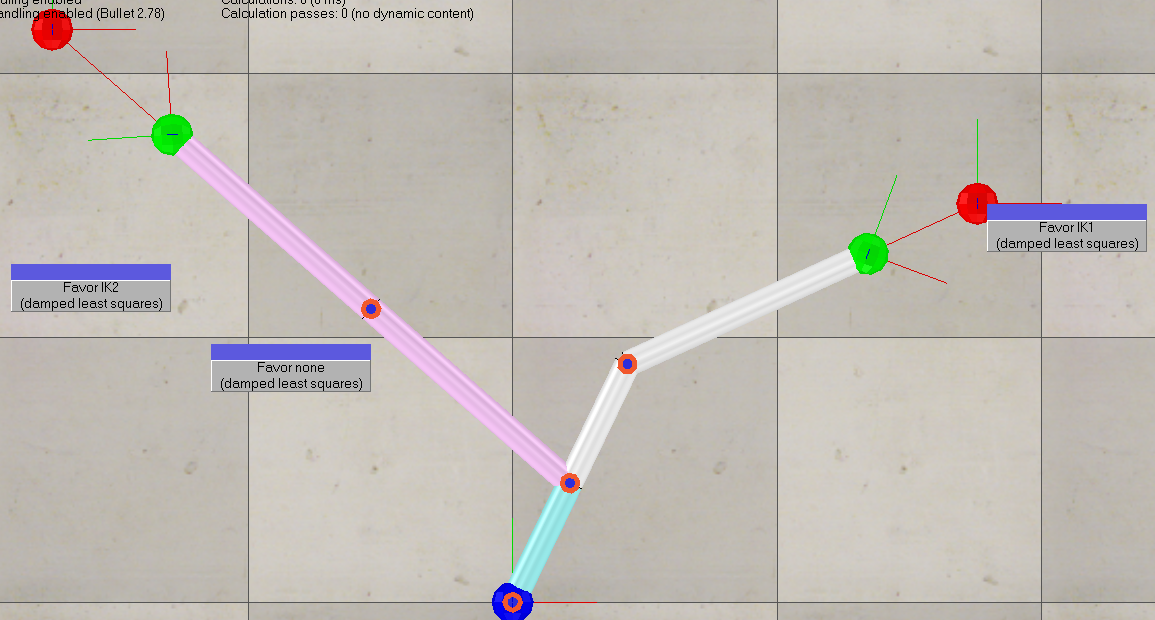
两个IK组的机制不共享关节，但是必须按照先解算IK1后解算IK2的顺序，否则就会造成下图的情况：

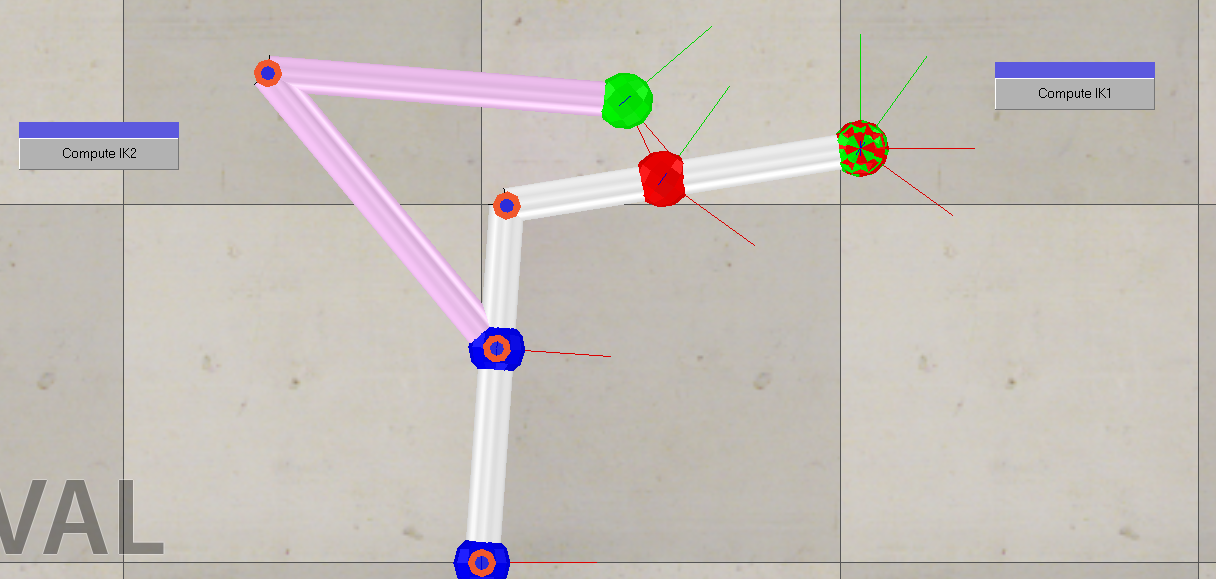
有共享关节的情况下，如果两个target可同时达到，则分两个IK组迭代反解算的效果 与在同一IK组内反解效果相同，否则需要在同一IK组内计算权重 并使tip分别指向target

数学推导

DH模型

坐标系定义

x i x_i xi​轴与 z i − 1 z_{i-1} zi−1​轴垂直并指向 z i + 1 z_{i+1} zi+1​轴

z i z_i zi​轴方向与第 i + 1 i+1 i+1个关节轴线重合

O i O_i Oi​为 z i z_i zi​轴与 z i − 1 z_{i-1} zi−1​轴交点或与两者公垂线交点

参数定义

关节角 θ \theta θ：关节旋转角度（关节旋转变量）， θ i \theta_i θi​为 x i x_i xi​轴与 x i − 1 x_{i-1} xi−1​轴夹角

连杆长度 a a a：两相邻关节轴的公垂线长度（固定参数）， a i − 1 a_{i-1} ai−1​为 z i z_i zi​轴与 z i − 1 z_{i-1} zi−1​轴公垂线长度

连杆偏置 d d d：两相邻x轴的距离（关节平移变量）， d i d_i di​为 x i x_i xi​轴与 x i − 1 x_{i-1} xi−1​轴距离

连杆扭转角 α \alpha α：连杆两端关节扭转角度（固定参数）， α i − 1 \alpha_{i-1} αi−1​为 z i z_i zi​轴与 z i − 1 z_{i-1} zi−1​轴夹角

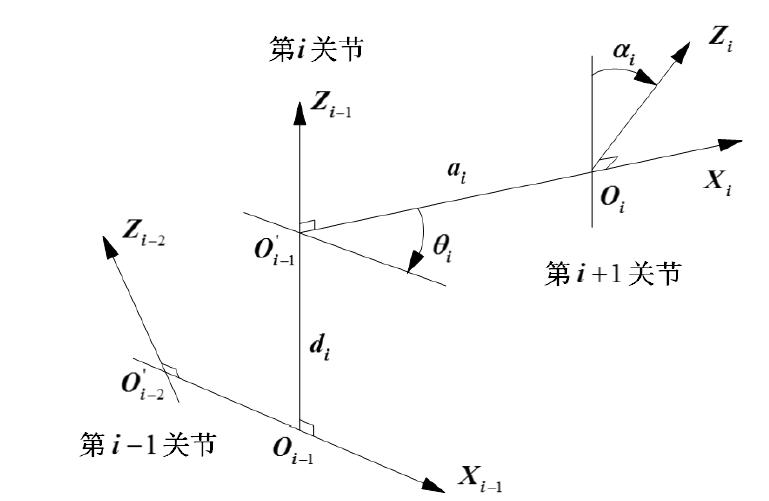
坐标变换

两个关节空间坐标系的平移旋转变换写为矩阵形式：
UR5为六自由度机械臂(即5连杆6关节)，则末端机械爪关节坐标系与基坐标系变换关系：
即为位姿变换基本矩阵

Jacobian矩阵

在向量微积分中，雅可比矩阵是一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。

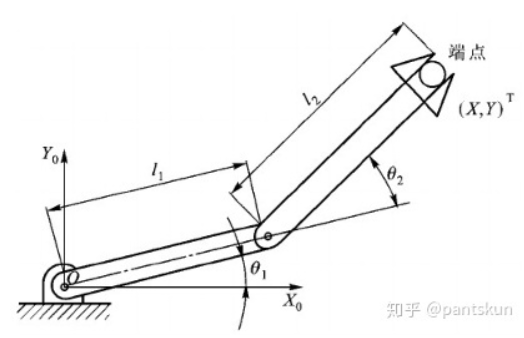
上图中端点位置坐标KaTeX parse error: \tag works only in display equations

雅各比矩阵 J = [ ∂ X ∂ θ 1 ∂ X ∂ θ 2 ∂ Y ∂ θ 1 ∂ Y ∂ θ 2 ] J = \begin{bmatrix} \frac{\partial X}{\partial \theta_1} & \frac{\partial X}{\partial \theta_2} \\ \frac{\partial Y}{\partial \theta_1} & \frac{\partial Y}{\partial \theta_2} \end{bmatrix} J=[∂θ1​∂X​∂θ1​∂Y​​∂θ2​∂X​∂θ2​∂Y​​]是函数 X , Y X,Y X,Y对于 θ 1 , θ 2 \theta_1,\theta_2 θ1​,θ2​的偏导数矩阵

则有微分形式 d V = [ d X d Y ] = J [ d θ 1 d θ 2 ] dV = \begin{bmatrix} dX \\ dY \end{bmatrix} = J \begin{bmatrix} d\theta_1 \\ d\theta_2 \end{bmatrix} dV=[dXdY​]=J[dθ1​dθ2​​]，简写为 d V = J d θ dV = J d\theta dV=Jdθ

三维空间端点广义位姿矩阵 V = { p x , p y , p z , α x , α y , α z } V = \{p_x,p_y,p_z,\alpha_x,\alpha_y,\alpha_z \} V={px​,py​,pz​,αx​,αy​,αz​}

六自由度角度矩阵 θ = { θ 1 , θ 2 , θ 3 , θ 4 , θ 5 , θ 6 } \theta = \{\theta_1,\theta_2,\theta_3,\theta_4,\theta_5,\theta_6\} θ={θ1​,θ2​,θ3​,θ4​,θ5​,θ6​}

广义雅各比矩阵 J = [ ∂ p x ∂ θ 1 . . . ∂ p x ∂ θ 6 ∂ p y ∂ θ 1 . . . ∂ p y ∂ θ 6 ∂ p z ∂ θ 1 . . . ∂ p z ∂ θ 6 ∂ α x ∂ θ 1 . . . ∂ α x ∂ θ 6 ∂ α y ∂ θ 1 . . . ∂ α y ∂ θ 6 ∂ α z ∂ θ 1 . . . ∂ α z ∂ θ 6 ] J = \begin{bmatrix} \frac{\partial p_x}{\partial \theta_1} & ... & \frac{\partial p_x}{\partial \theta_6} \\ \frac{\partial p_y}{\partial \theta_1} & ... & \frac{\partial p_y}{\partial \theta_6} \\ \frac{\partial p_z}{\partial \theta_1} & ... & \frac{\partial p_z}{\partial \theta_6} \\ \frac{\partial \alpha_x}{\partial \theta_1} & ... & \frac{\partial \alpha_x}{\partial \theta_6} \\ \frac{\partial \alpha_y}{\partial \theta_1} & ... & \frac{\partial \alpha_y}{\partial \theta_6} \\ \frac{\partial \alpha_z}{\partial \theta_1} & ... & \frac{\partial \alpha_z}{\partial \theta_6} \end{bmatrix} J=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡​∂θ1​∂px​​∂θ1​∂py​​∂θ1​∂pz​​∂θ1​∂αx​​∂θ1​∂αy​​∂θ1​∂αz​​​..................​∂θ6​∂px​​∂θ6​∂py​​∂θ6​∂pz​​∂θ6​∂αx​​∂θ6​∂αy​​∂θ6​∂αz​​​⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤​

通过求解 J − 1 J^{-1} J−1即可根据端点的运动得到关节的运动 d θ = J − 1 d V d\theta = J^{-1} dV dθ=J−1dV

CoppeliaSim

内置模块

使用CoppeliaSim内置运动学模块，通过GUI进行设置

范例

雅各比矩阵逆变换(Pseudo inverse)：

如果target位置过远或者为singular configuration，将会打破平衡，无法达成目标，如下图所示:

阻尼最小二乘法(damped least square method, DLS)：

更稳定(移动target位置，tip始终与target重叠或指向target)，但迭代次数更多

构建IK组

打开顶部导航栏Tools中的Scene Object Properties和Calculation Modules

在Scene Object Properties中将自由关节设为IK mode，选中tip将target添加为”linked dummy”并设置类型为“IK, tip-target”

在Calculation Modules中选择Kinematics选项卡，点击“add new IK group”，选择新建的IK组，点击下方“edit IK elements”，点击“add new IK element with tip”，选中tip并设置base，勾选其他Constraints section选项

API：sim.handleIkGroup

function sysCall_init()
    ikgroup=sim.getIkGroupHandle('IKGroup') --根据IK组名称更改
end
function sysCall_actuation()
    sim.handleIkGroup(ikgroup)
end

开启仿真即可进行逆解算，使tip与target重叠

外部编程

Coppelia Kinematics Routines，独立的C++例程

Coppelia运动学例程包装到一个插件simExtIK中，通过脚本函数(e.g. simIK.getConfigForTipPose)进行调用

Coppelia在程序启动时自动加载CoppeliaSimPro文件夹中的所有插件，也可在github下载

标签：partial,target,逆解算,机器人,frac,IK,关节,theta
来源： https://blog.csdn.net/xiaoxiangsss/article/details/113870199