题解-NOI2016 优秀的拆分
作者:互联网
\(T\) 组测试数据。求字符串 \(s\) 的所有子串拆成 \(AABB\) 形式的方案总和。
数据范围:\(1\le T\le 10\),\(1\le n\le 3\cdot 10^4\)。
这道题太神了,能一次做出这题的人往往是人形自走题库。真的全是套路!
令 \(n=|s|\),\(f_i\) 表示有几个以 \(s_i\) 结尾的 \(AA\) 串,\(g_i\) 表示有几个以 \(s_i\) 开头的 \(BB\) 串。
\[\therefore ans=\sum_{i=1}^{n-1}f_i\cdot g_{i+1} \]
然后只需求 \(f_i,g_i\)。
套路地为 \(s\) 以及 \(s\) 的反串建后缀数组并为 \(height\) 数组装上 \(st\) 表。
于是就可以 \(\Theta(1)\) 求任意两个前缀的最长公共后缀和任意两个后缀的最长公共前缀了。
这时候求 \(f_i\) 的 \(\Theta(n^2)\) 的做法(\(g_i\) 同):
枚举 \(A\) 串长度 \(w\),然后枚举 \(s\) 中的下标 \(l,r(r-l=w)\)。
如果两个后缀的最长公共前缀\(\ge w\),则 \(f_{r+w-1}++\)。
如下图,三条黄线间的两个串组成 \(AA\) 串。
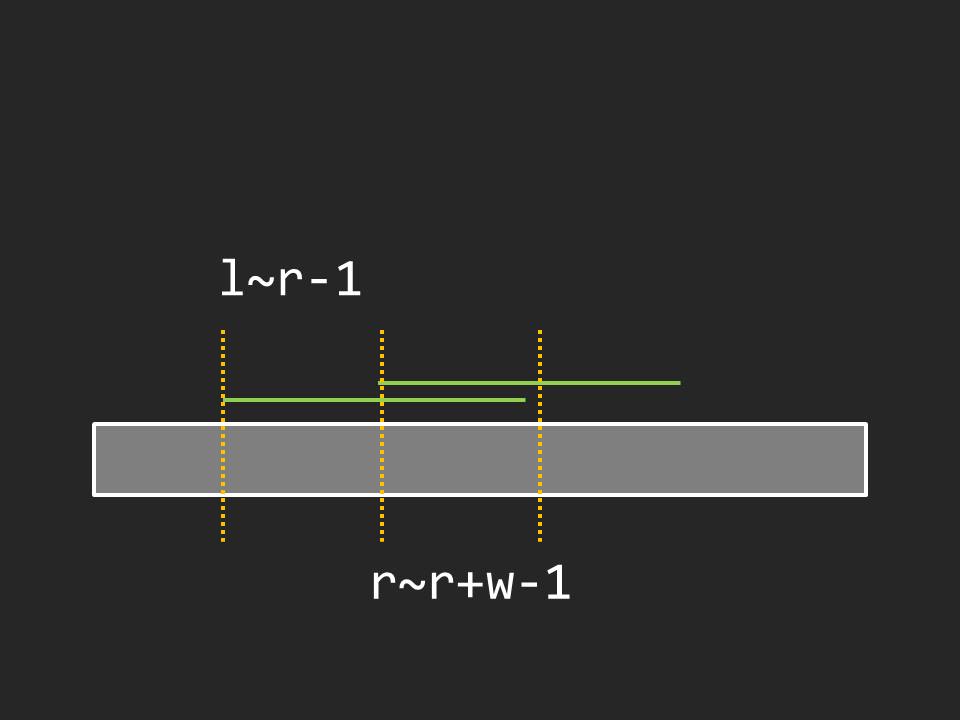
考虑一种套路优化(\(g_i\) 同):
枚举了 \(w\) 以后任何相距 \(w\) 的下标是对应的。
所以可以在 \(w\) 倍数的下标设断点,此时一个 \(A\) 串至少要经过 \(1\) 个断点。
枚举相邻两个断点 \(l\) 和 \(r\),求出它们的前缀最长公共后缀长度 \(lcs\) 和后缀最长公共前缀长度 \(lcp\) 之和 \(len\):
表示经过两个断点且开头距离 \(w\) 的最长公共子串。
如果 \(len<w\),说明没有同时经过这两个断点的 \(AA\) 串。
否则,\(f_{r+lcp-(lcp+lcs-1)\to r+lcp-1}++\)。
如下图,即两条紫线以及之间的子串为 \(AA\) 串:
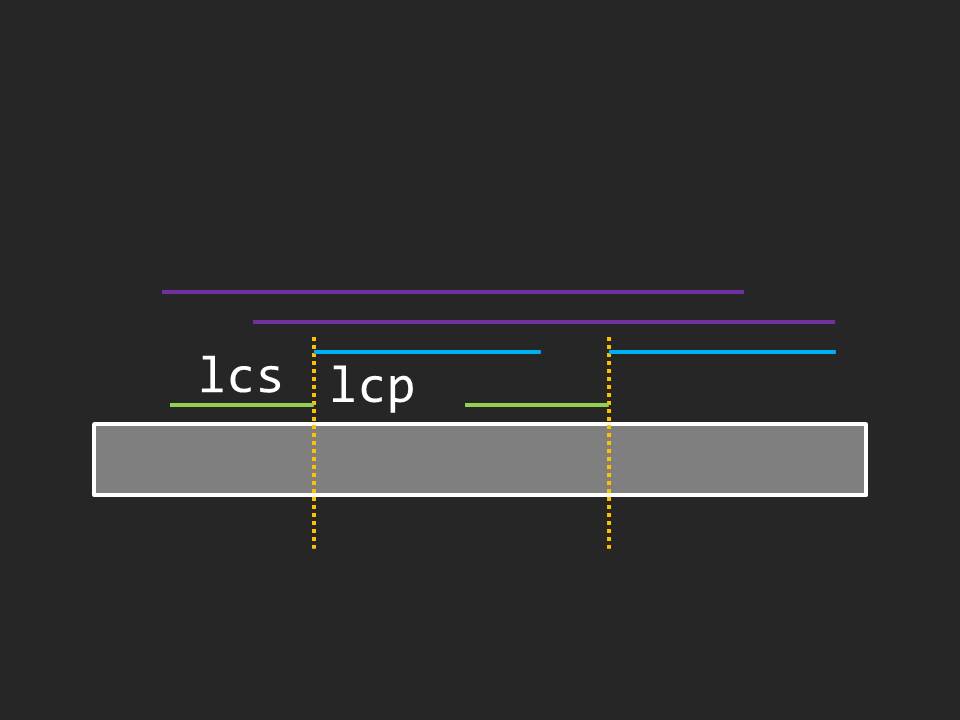
\(f_i,g_i\) 需要区间加,可以差分处理。
时间复杂度 \(\Theta(T\cdot n\log n)\)。
小蒟蒻讲不清楚,放代码吧:
#include <bits/stdc++.h>
using namespace std;
//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x first
#define y second
#define b(a) a.begin()
#define e(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;
//Data
const int N=3e4;
int n,f[N+7],g[N+7];
//SuffixArray
struct SuffixArray{
char s[N+7];
int m,c[N+7],tp[N+7],rk[N+7],sa[N+7];
int h[N+7],st[N+7][20];
void csort(){
for(int i=0;i<=m;i++) c[i]=0;
for(int i=1;i<=n;i++) c[rk[i]]++;
for(int i=1;i<=m;i++) c[i]+=c[i-1];
for(int i=n;i>=1;i--) sa[c[rk[tp[i]]]--]=tp[i];
}
void build(){
memset(c,0,sizeof c);
memset(tp,0,sizeof tp);
memset(rk,0,sizeof rk);
memset(sa,0,sizeof sa);
memset(h,0,sizeof h);
memset(st,0,sizeof st);
for(int i=1;i<=n;i++) rk[i]=s[i],tp[i]=i;
m=128,csort();
for(int w=1,p=1,i;p<n;w<<=1,m=p){
for(p=0,i=n-w+1;i<=n;i++) tp[++p]=i;
for(i=1;i<=n;i++)if(sa[i]>w) tp[++p]=sa[i]-w;
csort(),swap(rk,tp),rk[sa[1]]=p=1;
for(i=2;i<=n;rk[sa[i]]=p,i++)
if(tp[sa[i]]!=tp[sa[i-1]]||tp[sa[i]+w]!=tp[sa[i-1]+w]) p++;
}
for(int i=1,j,k=0;i<=n;h[rk[i++]]=k)
for(k=k?k-1:k,j=sa[rk[i]-1];s[i+k]==s[j+k];k++);
for(int i=1;i<=n;i++) st[i][0]=h[i];
for(int w=1;w<=18;w++)
for(int i=1;i+(1<<w)-1<=n;i++)
st[i][w]=min(st[i][w-1],st[i+(1<<(w-1))][w-1]);
}
int Lcp(int a,int b){
int l=rk[a],r=rk[b];
if(l>r) swap(l,r); l++;
int k=log2(r-l+1);
return min(st[l][k],st[r-(1<<k)+1][k]);
}
}a,b;
//KonnyWen
void KonnyWen(){
memset(f,0,sizeof f);
memset(g,0,sizeof g);
scanf("%s",&a.s[1]),n=strlen(&a.s[1]);
for(int i=1;i<=n;i++) b.s[i]=a.s[n+1-i];
a.build(),b.build();
for(int i=1;i<=n;i++) f[i]=g[i]=0;
for(int w=1;w<=(n>>1);w++)
for(int i=w;i<=n;i+=w){
int l=i,r=i+w;
int lcp=min(w,a.Lcp(l,r));
int lcs=min(w-1,b.Lcp(n-(l-1)+1,n-(r-1)+1));
if(lcp+lcs>=w){
int cov=lcp+lcs-w+1;
f[r+lcp-cov]++,f[r+lcp]--;
g[l-lcs]++,g[l-lcs+cov]--;
}
}
for(int i=1;i<=n;i++) f[i]+=f[i-1],g[i]+=g[i-1];
ll ans=0;
for(int i=1;i<n;i++) ans+=f[i]*g[i+1];
printf("%lld\n",ans);
}
//Main
int main(){
int t; scanf("%d",&t);
while(t--) KonnyWen();
return 0;
}
祝大家学习愉快!
标签:lcp,int,题解,memset,tp,++,NOI2016,拆分,define 来源: https://www.cnblogs.com/Wendigo/p/12930804.html