《 树状数组 》
作者:互联网
 的。
其实可以先跳到下面看Code的
既然ta是一种数据结构,那么也应该有一个模型吧?
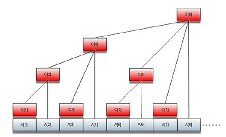
差不多就是这个样子吧……
开始
那上图代表什么意义呢?让我们开始讲一讲。
- \(C_1=A_1\)
- \(C_2=A_1+A_2\)
- \(C_3=A_3\)
- \(\ldots\ldots\)
不难看出 \(C\) 代表的是ta的子树对应所有 \(A\) 的和.(看不出来的再看)
其中有个特性:
- 设节点为 \(n\),那么这个节点管辖的区间为 \(2^k\) (其中 \(k\) 为 \(n\) 的二进制末尾 \(0\) 的个数)个元素。
- 所以:\(C_n=A_{n-2^k+1}+\ldots+A_n\)
好,那么该怎么做呢?
Code部分
lowbit
- 我们通常把 \(2^k\) 叫做 \(\texttt{lowbit(n)}\)
- 计算方法:
n&(-n) - 原理:计算机中的补码储存方式
树状数组中最重要的东西,也是实现Code的重心。
标签:Code,img,树状,lowbit,数组,ldots 来源: https://www.cnblogs.com/Cnghit/p/16465579.html