其他分享
首页 > 其他分享> > color flip

color flip

作者：互联网

886. Possible Bipartition Medium

We want to split a group of n people (labeled from 1 to n) into two groups of any size. Each person may dislike some other people, and they should not go into the same group.

Given the integer n and the array dislikes where dislikes[i] = [ai, bi] indicates that the person labeled ai does not like the person labeled bi, return true if it is possible to split everyone into two groups in this way.

 Example 1:

Input: n = 4, dislikes = [[1,2],[1,3],[2,4]]
Output: true
Explanation: group1 [1,4] and group2 [2,3].

Example 2:

Input: n = 3, dislikes = [[1,2],[1,3],[2,3]]
Output: false

Example 3:

Input: n = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
Output: false

Constraints:

解题思路：

1.将dislike建图

2.对所有节点进行dfs遍历，每次传递并且切换颜色，如果传入的期望颜色与已标颜色出现冲突，说明不满足条件

class Solution {
    public boolean possibleBipartition(int n, int[][] dislikes) {
        //build graph  建图
        List<Integer>[] graph = new List[n+1];
        for(int i=0;i<=n;i++) graph[i] = new ArrayList();
        for(int[] dislike : dislikes){
            int left = dislike[0],right = dislike[1];
            graph[left].add(right);
            graph[right].add(left);
        }
        //init color array
        int[] colors = new int[n+1];
        Arrays.fill(colors, -1);
        int count = 0;
        for(int i=0;i<=n;i++){
            if(colors[i]==-1){
                if(!dfs(graph, colors, i, 0)) return false;
            }
        }
        return true;
    }
    private boolean dfs(List<Integer>[] graph, int[] colors, int curr, int color){
        if(colors[curr]!=-1){
            if(colors[curr]==color) return true;
            else return false;
        }
        colors[curr] = color;
        for(int other:graph[curr]){
            if(!dfs(graph, colors, other, 1-color)) return false;
        }
        return true;
    }
}
785. Is Graph Bipartite? Medium

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

 Example 1:

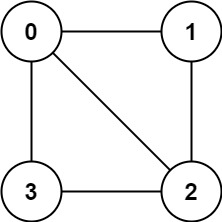
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

 Constraints:

解题思路：

跟上一题类似，但是记得把所有点都过一遍，以免不联通的图 漏掉一些group

class Solution {
    public boolean isBipartite(int[][] graph) {
        int[] color = new int[graph.length];
        Arrays.fill(color,-1);
        for(int i=0;i<graph.length;i++){//坑点，有可能这个图压根就不连通，因此需要把所有点都过一遍
            if(color[i]==-1){
                if(!dfs(graph, i, color, 0)) return false;
            }
        }
        return true;
    }
    private boolean dfs(int[][] graph, int node, int[] color, int nextColor){
        if(color[node]!=-1 ) return color[node]==nextColor;
        color[node] = nextColor;
        for(int other:graph[node]){
            if(!dfs(graph, other, color, 1-nextColor)) return false;
        }
        return true;
    }
}



标签：node,color,graph,dislikes,flip,int,nodes
来源： https://www.cnblogs.com/cynrjy/p/16462506.html