初等数论学习笔记 II
作者:互联网
1. Miller-Rabin
Miller-Rabin 素性测试是常见的 随机性 素数判定方法。
这里的随机指有一定概率将合数判定为素数,但不会将素数判定为合数。
素数判定的基本思路是,根据所有质数均具有但很少合数具有的性质,检查被判定的数是否具有这些性质。若不具有,则可断定该数是合数,否则该数有很大概率是质数(但并不确定)。
1.1 Fermat 素性检验
我们知道,当 \(p\) 是素数时,对于任意 \(a \perp p\) 均有 \(a ^ {p - 1}\equiv 1 \pmod p\)。反之,当 \(a ^ {p - 1} \equiv 1\pmod p\) 时,是否有 \(p\) 是素数?如果命题成立,那么判断一个数是否是素数只需要一遍快速幂。
可惜命题并不成立。有很小的概率使得 \(a \perp p\),\(p\) 是合数且 \(a ^ {p - 1} \equiv 1\pmod p\),例如当 \(a = 2\),\(p = 341\) 时,\(2 ^ {340} \equiv 1 \pmod {341}\)。这种情况称为 \(341\) 是以 \(2\) 为底的伪素数。\(341\) 是最小的伪素数基数。
但是若 \(a ^ {p - 1}\not \equiv 1\pmod p\),则 \(p\) 必然不是质数。为此,考虑多选几个与 \(p\) 互质的数检查,这样可以排除大部分合数。这被称为 Fermat 素性检验。显然,它带有随机性。
当面对形如 \(561\) 的卡迈克尔数时,Fermat 素性检验就束手无策了,因为卡迈克尔数 \(p\) 满足所有与 \(p\) 互质的数的 \(p - 1\) 次方模 \(p\) 均为 \(1\)。这说明 Fermat 素性检验仍不够优秀。
1.2 二次探测定理
根据高次剩余部分的知识,当 \(p\) 为奇素数时,\(x ^ 2\equiv 1\pmod p\) 仅有解 \(\pm 1\)。因此,对于 \(p\) 而言,若存在 \(a \neq \pm 1\) 满足 \(a ^ 2 \equiv 1\pmod p\),则 \(p\) 必然不是质数。
这被称为二次探测定理。
1.3 算法介绍
考虑将二次探测定理和费马素性检验合起来用。
根据二次探测定理,当 \(a ^ {p - 1} \equiv 1\pmod p\) 时,若 \(p - 1\) 是 \(2\) 的倍数,则 \(a ^ {\frac {p - 1} 2}\) 必须是 \(\pm 1\)。若 \(\dfrac {p - 1} 2\) 仍是 \(2\) 的倍数且 \(a ^ {\frac {p - 1} 2}\equiv 1\pmod p\),则 \(a ^ {\frac {p - 1} 4}\) 必须是 \(\pm 1\),以此类推。
简单地说,若 \(p - 1\) 是 \(2 ^ r\) 的倍数且 \(a ^ {\frac {p - 1}{2 ^ {r - 1}}} \equiv 1\pmod p\),则 \(a ^ {\frac {p - 1}{2 ^ r}}\) 必须等于 \(\pm 1\),否则就不是素数。
例如 \(a = 2\) 且 \(p = 341\)。\(2 ^ {340} \equiv {341}\),\(2 ^ {170} \equiv 1\pmod {341}\),但 \(2 ^ {85} \equiv 32\pmod {341}\)。这说明 \(341\) 不是质数。
这样检测的准确率相当高。事实上,随机选择 \(k\) 个底数,则 Miller-Rabin 算法的正确性(指不会将合数误判成素数的概率)为 \(1 - 4 ^ {-k}\),时间复杂度为 \(\mathcal{O}(k \log ^ 2 n)\)(若将快速幂视为一个 \(\log\) 而非关于值域的三个 \(\log\))。
注意到 Miller-Rabin 的效率和选取底数个数有关,我们自然希望底数越少越好,同时要保证一定的正确性。以下是常用底数(来自 wangrx 的博客,在此感谢他)。
- 对 \(2 ^ {32}\) 以内的数判素,使用 \(2, 7, 61\) 三个底数。
- 对 \(2 ^ {64}\) 以内的数判素,使用 \(2,325,9375,28178,450775,9780504,1795265022\) 七个底数。
- 使用前 \(12\) 个素数作为底数可以对 \(318665857834031151167460(3\times 10 ^ {23} \approx 2 ^ {78})\) 以内的数判素。详见 A014233 - OEIS。
- 注意,在固定底数时,需要对底数特判。即若以 \(2, 7, 61\) 作为底数,则当 \(n = 2, 7\) 或 \(61\) 时需直接特判通过检验,因为 \(p\) 无法通过以 \(p\) 为底的素性检验。
mt19937 rnd(time(0));
#define ll long long
int rd(int l, int r) {return rnd() % (r - l + 1);}
ll ksm(ll a, ll b, ll p) {
ll s = 1;
while(b) {
if(b & 1) s = (__int128) s * a % p;
a = (__int128) a * a % p, b >>= 1;
}
return s;
}
bool Miller_Rabin(ll n) {
if(n < 3 || n % 2 == 0) return n == 2;
for(int i = 1; i <= 10; i++) {
int x = rd(1, 1e9) % (n - 2) + 2;
if(ksm(x, n - 1, n) != 1) return 0;
for(ll j = n - 1; j & 1 ^ 1;) {
ll val = ksm(x, j >>= 1, n);
if(val == n - 1) break;
if(val != 1) return 0;
}
}
return 1;
}
1.4 复杂度优化
Miller-Rabin 的复杂度和正确性足够优秀,但我们注意到在整个过程中我们多次使用快速幂计算 \(a\) 的幂,且指数每次除以 \(2\)。这很浪费。
考虑将整个过程反过来,即预先处理好 \(p - 1 = r \cdot 2 ^ d\),然后计算 \(a ^ r\) 并执行 \(d\) 次平方操作,即可得到每个 \(a ^ {r \cdot 2 ^ i}\)。这样,时间复杂度优化为 \(\mathcal{O}(k\log n)\),尽管在 OI 中应该没有毒瘤出题人会扣这个细节。
更进一步地,首先判掉 \(a ^ r\equiv 1\pmod p\),此时 \(p\) 通过了本轮检验(但并不一定是素数)。否则若 \(p\) 是质数,说明在 \(i\) 从 \(d\) 减小到 \(0\) 的过程中,\(a ^ {r \cdot 2 ^ i}\bmod p\) 必然经历了从 \(1\) 变为 \(-1\) 的过程(如果 \(a ^ {r \cdot 2 ^ d} \not\equiv 1\pmod p\),则 \(p\) 甚至没有通过 Fermat 素性检验)。
因此,我们只需判断是否存在 \(0\leq i < d\) 使得 \(a ^ {r \cdot 2 ^ i} \equiv -1 \pmod p\)。容易证明这是 \(p\) 通过该轮素性检验的充要条件。
bool Miller_Rabin(ll n) {
if(n < 3 || n % 2 == 0) return n == 2;
ll r = n - 1, d = 0;
while(r & 1 ^ 1) r >>= 1, d++;
for(int i = 1; i <= 10; i++) {
ll x = rd(1, 1e9) % (n - 2) + 2, v = ksm(x, r, n);
if(v == 1) continue;
for(int j = 0; j <= d; j++) {
if(j == d) return 0;
if(v == n - 1) break;
v = (__int128) v * v % n;
}
}
return 1;
}
2. Pollard-rho
分解质因数一般使用的试除法的时间复杂度为 \(\mathcal{O}(\sqrt n)\),因为我们必须枚举到 \(\sqrt n\) 才能确定 \(n\) 是一个质数。
Pollard-rho 算法为时间复杂度又开了一次平方,它可以在期望 \(\sqrt[4]{n}\) 的时间复杂度内求出 \(n\) 的一个非平凡因子。因此使用 Pollard-rho 分解质因数的时间复杂度为 \(\sqrt [4]{n}\omega(n)\)。
2.1 生日悖论
相信读者都或多或少了解过这一悖论,这里简单讲一下。
从 \(1\sim n\) 的正整数中 \(k\) 次等概率随机选出一个数(可重复),则所有数互不相同的概率为
\[P = \dfrac {n ^ {\underline{k}}} {n ^ k} \]这个公式的含义是从 \(n\) 个数中有序地 \(k\) 个数的方案数除以总方案数。
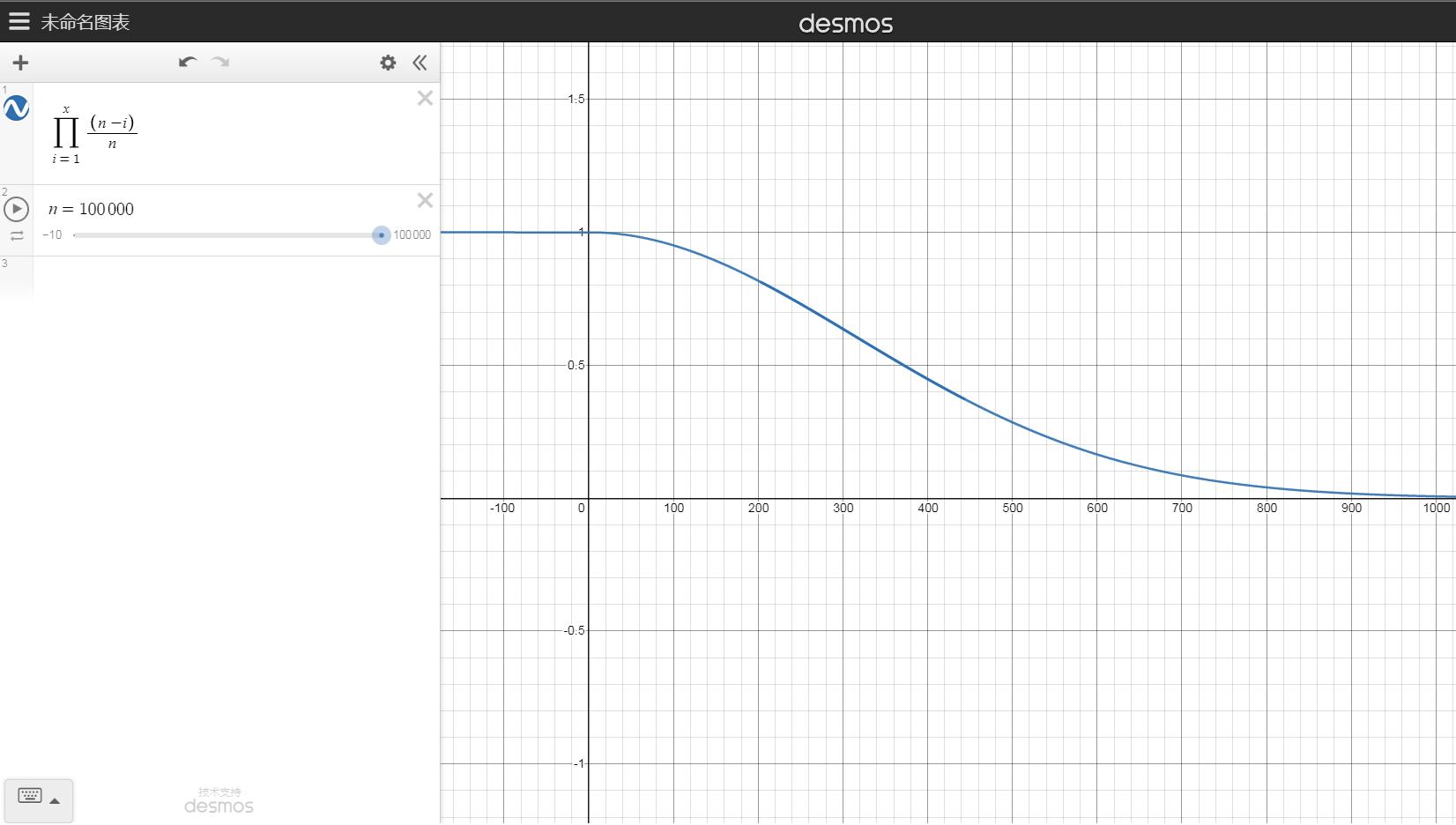
- 直观认知:当 \(k\) 增大时,\(P\) 衰减得相当快,因为每次 \(\dfrac {n - k + 1} n\) 均以相乘的方式作用在 \(P\) 上。可以理解为指数衰减,但没有指数衰减那么快,因为分子也相当大。如下图。
经过手玩函数图像后,我们发现使得 \(P = \dfrac 1 2\) 的 \(k\) 似乎是 \(\sqrt n\) 级别的。
证明详见 OI Wiki,我们只需要记住结论:每次在 \(n\) 个数中等概率随机选择一个,使得所有选出的数中存在两个相同的期望次数为 \(\mathcal{O}(\sqrt n)\)。
2.2 算法介绍
Pollard-rho 算法的巧妙之处在于构造伪随机函数 \(f(x) = x ^ 2 + c\)。
因为 \(f\) 仅含有一个变量,因此对于相同的 \(x\),\(f(x)\) 给出的值也均相同。选取 \(f\) 的好处是在进入循环前,不断迭代得到的数可近似看做随机。其随机性不作证明(也许和曼德勃罗集的混沌属性有关)。
根据生日悖论,在模 \(n\) 意义下,若给定 \(c\) 和初始值 \(x_0\)(一般以 \(0\) 作为初始值),则 \(f\) 在不断迭代的过程中(即 \(x_0, x_1= f(x_0), x_2 = f(x_1), \cdots, f_i = f ^ i(x)\),\(x_i\) 均对 \(n\) 取模)期望 \(\sqrt n\) 次进入一个长为 \(\sqrt n\) 的循环。
因为整条路径酷似希腊字母 \(\rho\),算法得名 Pollard-rho。记 \(x_i\) 在模 \(n\) 意义下形成的路径为 \(\rho_n\),如下图。
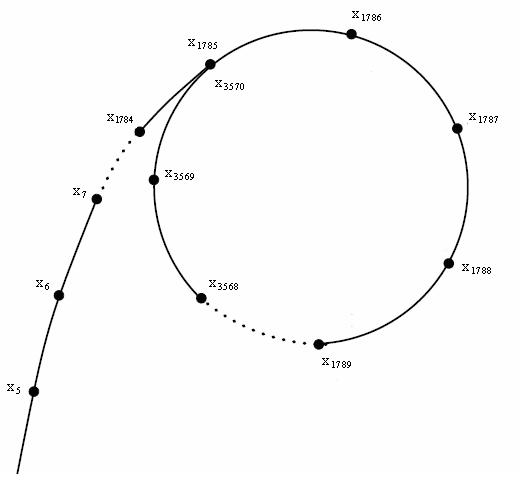
若 \(n\) 为合数,则其最小非平凡因子 \(m\) 的级别不超过 \(\sqrt n\)。这说明在模 \(m\) 意义下 \(x_i\) 期望 \(\sqrt [4]{n}\) 次进入一个长为 \(\sqrt [4]{n}\) 的循环。记 \(x_i\) 在模 \(n\) 意义下形成的路径为 \(\rho_m\)。
同时,若模 \(m\) 一旦进入循环(即存在 \(x_i \equiv x_j\pmod m\)),我们就可以通过将 \(|x_i - x_j|\) 和 \(n\) 取 \(\gcd\) 来求出 \(m\)(或者它的倍数),前提是 \(x_i \not\equiv x_j\pmod n\)。
现在的问题是求出一组 \(i, j\) 使得 \(i, j\) 处于 \(\rho_m\) 上的同一点,但处于 \(\rho_n\) 上的不同点。也就是,\(i\) 需要足够大(据分析,级别为 \(\sqrt [4]{m}\)),使得跳出 \(\rho_m\) 的尾巴,且 \(j - i\) 恰好是 \(\rho_m\) 的循环节的倍数。
注意在整个过程中我们不知道 \(m\),但通过分析可以证明求得 \(m\) 的的期望复杂度为 \(\sqrt [4]{n}\)(我们将说明如何去掉 \(\gcd\) 的 \(\log\) 因子)。求得的非平凡因子也不一定最小,因此还需继续分解。
介绍两个解决上述问题的常见方法。
考虑直接令 \(j = 2i\),然后从小到大枚举 \(i\),不断计算 \(\gcd(|x_{2i} - x_i|, n)\) 直到该值不等于 \(1\)。
此时有两种情况,一是小于 \(n\),这说明该值即 \(n\) 的一个非平凡因子,直接返回。二是等于 \(n\),这说明我们进入了 \(\rho_n\) 的循环节,有很大概率 \(\rho_n\) 的环长等于 \(\rho_m\) 的环长,也有可能是 \(\rho_m\) 的尾巴过长,使得第一次在枚举到 \(\rho_m\) 的环长的倍数使得 \(i\) 跳出 \(\rho_m\) 的尾巴时就枚举到了 \(\rho_n\) 的环长。无论如何,这意味着我们应该结束本次失败的 Pollard-rho,调整参数 \(c\) 重新分解。 期望时间复杂度 \(\sqrt [4]{n} \log n\)。
上述算法被称为基于 Floyd 判环的 Pollard-rho 算法。
- Note:笔者在实现了 Floyd 判环后,发现若初始令 \(i = 1\),\(j = 2\),则对于 \(n = 4\) 无论如何也分解不出来。需要初始令 \(i = 0\),\(j = 1\)(或特判 \(n = 4\)),然后每次 \(i \gets i + 1\),\(j \gets j + 2\)。
优化:注意到 \(\gcd\) 调用次数过多会显著降低效率,朴素的 Floyd 判环法无法通过模板题。我们考虑设置 “样本累计上限” \(T\),将 \(T\) 组 \(\gcd\) 测试打包在一起,其正确性基于 \(\gcd(a, n) \mid \gcd(ab\bmod n, n)\)。\(T\) 取 \(10\) 时在模板题数据下表现较为优秀。这样可以将复杂度中的 \(\log\) 因子去掉。
ll n, c, s, t;
ll f(ll x) {return ((__int128) x * x + c) % n;}
ll Pollard_rho(ll _n) {
n = _n, c = rd(0, 1e9) % ((n = _n) - 1) + 1, s = f(t = 0); // 注意 t = 0 而不能 t = c
ll acc = 0, prod = 1, d;
while(s != t) {
prod = (__int128) prod * abs(s - t) % n;
if(++acc == 10) {
if((d = __gcd(prod, n)) > 1) return d;
acc = 0;
}
s = f(f(s)), t = f(t);
}
if((d = __gcd(prod, n)) > 1) return d;
return n;
}
二分一个未知上界的数的最好方法是倍增。于是我们固定 \(i = 2 ^ k\),\(j\) 取遍 \([2 ^ k + 1, 2 ^ {k + 1}]\),检查即可。同样的,需要考虑到 \(i = 0\),\(j = 1\) 的情况,或特判 \(n = 4\)。
倍增法也需要样本累计优化加持,即每 \(T\) 组 \(|x_i - x_j|\) 样本打包在一起,相乘后求 \(\gcd\)。对于倍增法而言,通常使用 \(T = 127\)。代码见例题 I.
- Note:如果担心 \(n\) 较小时算法的正确性,可以暴力分解质因数。读者需要认识到 Pr 本身是一个随机算法的本质。对于一些广为流传的 Pr 写法,前人已经验证过了其在一定范围内的正确性,所以我们只需放心大胆地使用即可。
总之,求解 \(i, j\) 的方法多种多样,但样本累计优化去掉 \(\log\) 因子是核心。检查太耗时则将若干次检查打包在一起,这样的思想方法不仅可用于优化 Pollard-rho,也可以应用在 OI 的其他各个领域。
2.3 例题
I. P4718【模板】Pollard-Rho 算法
#include <bits/stdc++.h>
using namespace std;
mt19937 rnd(time(0));
#define ll long long
int rd(int l, int r) {return rnd() % (r - l + 1);}
ll ksm(ll a, ll b, ll p) {
ll s = 1;
while(b) {
if(b & 1) s = (__int128) s * a % p;
a = (__int128) a * a % p, b >>= 1;
}
return s;
}
bool Miller_Rabin(ll n) {
if(n < 3 || n % 2 == 0) return n == 2;
ll r = n - 1, d = 0;
while(r & 1 ^ 1) r >>= 1, d++;
for(int i = 1; i <= 10; i++) {
ll x = rd(2, n - 1), v = ksm(x, r, n);
if(v == 1) continue;
for(int j = 0; j <= d; j++) {
if(j == d) return 0;
if(v == n - 1) break;
v = (__int128) v * v % n;
}
}
return 1;
}
ll Pollard_rho(ll n) {
ll c = rd(1, n - 1), s = 0, t = 0, prod = 1;
for(int i = 1; ; s = t, i <<= 1)
for(int j = 1; j <= i; j++) {
t = ((__int128) t * t + c) % n, prod = (__int128) prod * abs(s - t) % n;
if((j % 127 == 0 || j == i) && __gcd(prod, n) > 1) return __gcd(prod, n);
}
}
ll maxprime(ll n) {
if(n == 1) return 1;
if(Miller_Rabin(n)) return n;
ll p = Pollard_rho(n);
while(p == n) p = Pollard_rho(n);
while(n % p == 0) n /= p;
return max(maxprime(p), maxprime(n));
}
int main() {
ll T, n;
cin >> T;
while(T--) {
cin >> n;
if(Miller_Rabin(n)) {puts("Prime"); continue;}
cout << maxprime(n) << endl;
}
return 0;
}
3. 参考资料
第一章:
第二章:
标签:return,数论,ll,sqrt,II,pmod,rho,初等,equiv 来源: https://www.cnblogs.com/alex-wei/p/Number_Theory_II.html