蒙特卡洛模拟
作者:互联网
原文链接:这里
0.什么是蒙特卡洛模拟
蒙特卡洛模拟也称为随机抽样法或统计实验法,是一种以统计理论为指导的风险分析技术,它的实质是按一定概率分布产生随机数的方法,来模拟可能出现的随机现象。由于各个自变量参数的状态概率值是通过大量的客观统计抽样得到的,所以又称客观概率法
1.原理介绍
在一个简单的销售关系中,评价指标Y(假定为总利润或收益率等)是自变量Xi(X1,X2,X3,……,Xi) (可以分别表示产量,售价,成本,运输费等等)的多元函数关系。即:
,,,Z=f(X1,X2,X3,……Xi)
根据大量的统计资料,分别确定各个自变量参数的概率分布,并根据每一个自变量的概率分布情况,确定其所产生随机数的分布,在此基础上,分别随机取得各个变量的一个样本值,来计算一次目标函数。
简言之就是统计多因素同时变化对于评价指标的影响。
2.工具及方法
使用蒙特卡洛模拟比较有名的工具是Crystal Ball(水晶球),使用水晶球要配合excel,它是excel的一个插件。使用水晶球的主要步骤是:
(1)建立电子表格模型
(2)规定关于概率变量的假设
(3)规定预测单元,即有关输出变量
(4)设定重复次数
(5)运行模拟
(6)解释结果
3.蒙特卡洛一些案例
(1)概率类问题
拿最简单的一个扔色子的案例来解释一下。假设现在有两个色子,需要统计同时出现色子为两个6这个事件N,然后一共投了M次,用N除以M就是结果。在这个例子中,蒙特卡洛会做的是先大量模拟扔色子,并记录同时出现两个6的次数。然后用发生次数除以总次数就得出结果了。

(2)数学求近似解
我们求一下f(x)=x3在[0,2]上的积分,我们用蒙特卡洛的方法实现一下,
import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 2, 1000) y = x ** 3 plt.plot(x, y) plt.fill_between(x, y, where=(y > 0), color='red', alpha=0.5) plt.show()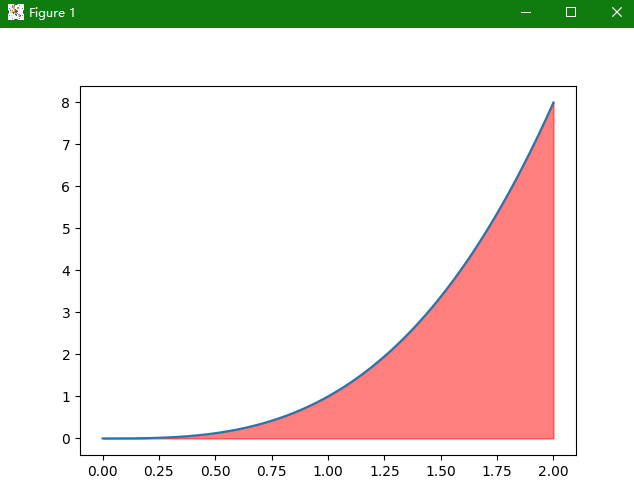
整个区域在一个2*8的方块里面,我们用蒙特卡洛方法进行模拟,模拟1000个点,看看有多少点落在红色里面,(用count表示落在红色区域的数量,用N表示总数量)
import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 2, 1000) y = x ** 3 plt.plot(x, y) plt.fill_between(x, y, where=(y > 0), color='red', alpha=0.5) N = 1000 points = [[xy[0] * 2, xy[1] * 8] for xy in np.random.rand(N, 2)] plt.scatter([x[0] for x in points], [x[1] for x in points], s=5, c=np.random.rand(N), alpha=0.5) plt.show()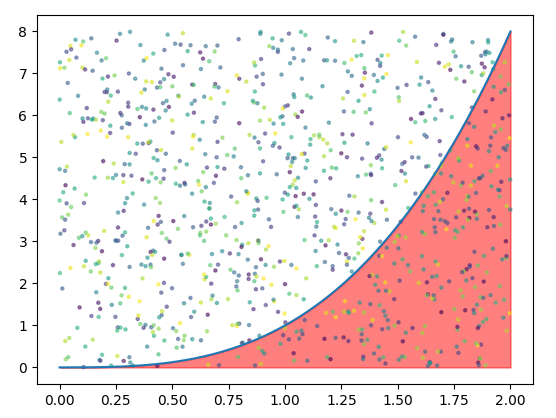
然后计算红色区域占的比重
import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 2, 1000) y = x ** 3 plt.plot(x, y) plt.fill_between(x, y, where=(y > 0), color='red', alpha=0.5) N = 1000 points = [[xy[0] * 2, xy[1] * 8] for xy in np.random.rand(N, 2)] plt.scatter([x[0] for x in points], [x[1] for x in points], s=5, c=np.random.rand(N), alpha=0.5) count = 0 for xy in points: if xy[1] < xy[0] ** 3: count += 1 print((count / N) * (2 * 8))程序运行10次,结果分别是
4.224 4.112 3.84 3.68 3.872 3.984 3.92 4.192 4.096 3.808可以看出与正确结果4相差0.2左右。如果模拟次数改成10000次,运行10次结果分别是
4.0544 3.9248 4.0064 3.9072 4.0176 4.1264 4.0256 4.008 4.008 4.0624 可以看出,随着模拟次数的增加,模拟答案越来越接近正确值。也就是样本的数量越大,误差越小。
标签:plt,points,xy,np,蒙特卡洛,模拟 来源: https://www.cnblogs.com/longkui-site/p/15858056.html