solution-uva10918
作者:互联网
题意:
一个3×n的棋盘用1×2的小长方形完全覆盖有几方案?
易得n为奇数时,方案数为0。
那为偶数是该怎么做?(以下均只考虑n为偶数的情况)
我们令f[i]表示n为i是的情况数,
此时,f[2] = 3。
我们两行两行的来看,每单独两行的情况数为3。那么根据排列组合,f[i]是不是等于f[i-2]×3?
显然不是!
反例:
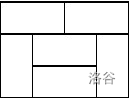
此时,n=4。这四行被连起来了!
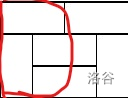
左边这两行不再作为单独考虑!
但好消息是,连起来的只有两种种可能,一种如上图,一种就是把上图倒过来。
连起来是中间部分都只有一种可能,不然会“断开”。
下图为更大的一种连起来的块:
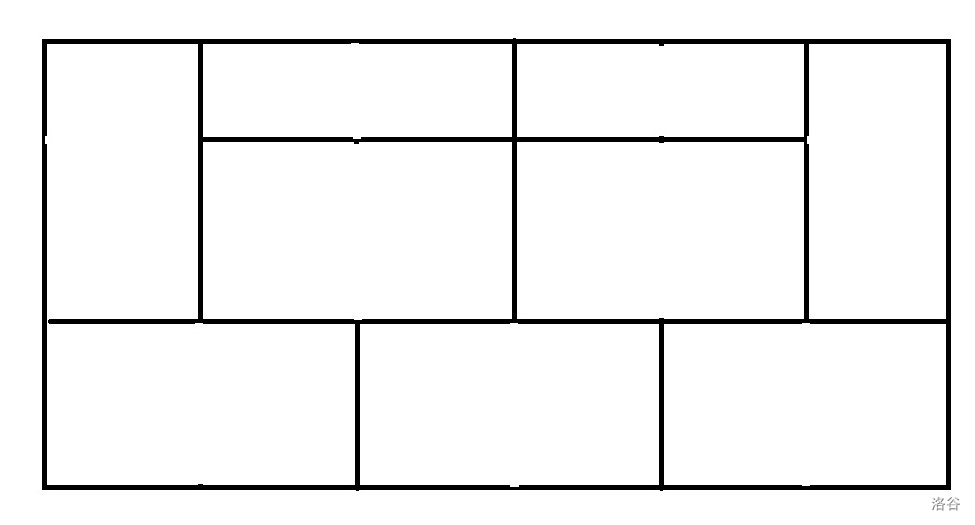
所以我们不妨枚举从i开始连起来的长度。
长度从4到n的所有偶数都有可能!
所以f[i] = f[i-2]×3 + 2×(f[i-4] + f[i-4-2×1] + f[i-4-2×2]+......+f[0])。
代码如下:
首先先把f[0]到f[30]的表预处理:
#include<iostream>
using namespace std;
long long f[40];
int main()
{
f[0] = 1;
f[2] = 3;
for(int i = 3; i <= 30; i++)
{
if(f[i]%2) continue;
f[i] += f[i-2] * 3;
for(int j = 4; j <= i; j+=2)
{
f[i]+=f[i-j]*2;
}
}
for(int i = 0; i <= 30; i++){
cout<<f[i]<<",";
}
return 0;
}
最后再按题目输入输出:
#include<iostream>
using namespace std;
int f[31] = {1,0,3,0,11,0,41,0,153,0,571,0,2131,0,7953,0,29681,0,110771,0,413403,0,1542841,0,5757961,0,21489003,0,80198051,0,299303201};
int main()
{
int n;
while(cin>>n){
if(n==-1) return 0;
cout<<f[n]<<endl;
}
}
完结撒花!
标签:两行,int,数为,solution,偶数,uva10918,using,include 来源: https://www.cnblogs.com/WRuperD/p/15703453.html