牛顿迭代法

什么是牛顿迭代法

牛顿-拉弗森方法 Newton-Raphson method 用来近似求解多项式的根

公式

顾名思义,该方法采用迭代的思想,已知曲线方程\(f(x)\), 在\(x_n\)点做切线,求\(x_{n+1}\)
在\(x_n\)点的切线方程为

\[f(x_n)+f'(x_n)(x-x_n) \]

那么\(x_{n+1}\)即为

\[f(x_n)+f'(x_n)(x_{n+1}-x_n)=0\\ x_{n+1}=x_n-\frac {f(x_n)} {f'(x_n)} \]

从泰勒展开的角度理解

\[f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac {f"(\xi)(x-x_0)^2} {2!} \]

忽略二次项

\[f(x) \approx f(x_0)+f'(x_0)(x-x_0) \]

从这个式子也可以看出,在使用牛顿迭代法时,需要选取一个较为解接近真实解的\(x_0\)作为迭代基数,\(x_0\)要在\(x\)附近

牛顿迭代法的问题

牛顿迭代法不是总能收敛的,所以在某些情况下找不到足够近似的根

驻点

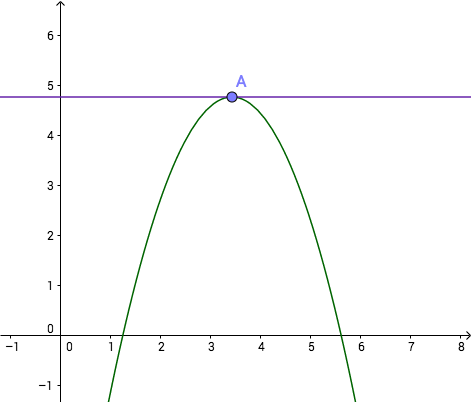
越来越远离

此处根点很显然是0点,而\(f'(0)\)不存在

循环震荡

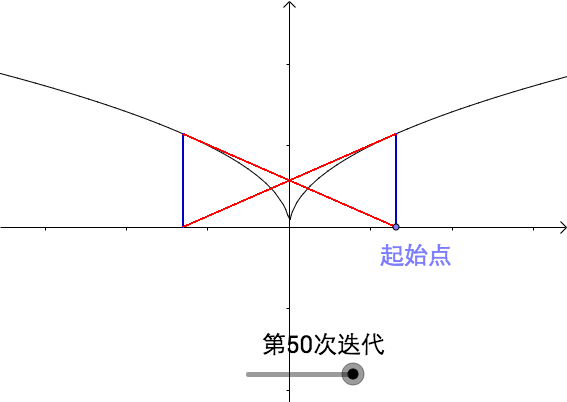
这种情况\(x_{n+1}=-x_n\)

不能完整求出所有的根

这种有多个根的函数，因为选择的起始点，只能求到附近的根

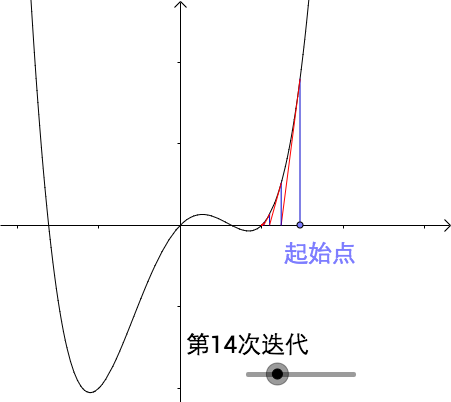
总结

函数在整个定义域内最好是二阶可导的

起始点对求根计算影响重大，可以增加一些别的判断手段进行试错

求平方根用牛顿-拉弗森方法是安全的

Reference

https://www.zhihu.com/question/20690553

标签：frac,迭代,切线,牛顿,拉弗,迭代法
来源： https://www.cnblogs.com/xiaoqian-shen/p/15487364.html