参考教材：《Modern Control Engineering 5th Edition》Katsuhiko Ogata

第02章 动态系统的数学模型

简单了解状态空间表示（State Space Representation）

教材上p35-39介绍了一个通用的方法，不过因为SSR不是本学期的重点，所以课上没讲，自己所以也暂时没有细看。

通过设置合适的变量，可以将高阶微分方程（组）改写为一阶微分方程组，再以向量的形式表示就得到了该系统的SSR：

\[\left\{ \begin{aligned} \dot{\boldsymbol{x}}(t) &=A \boldsymbol{x}(t)+\boldsymbol{b} u(t) \\ y(t) &=\boldsymbol{c}^{T} \boldsymbol{x}(t)+d u(t) \end{aligned} \right. \]

还可以写向量化更彻底的形式：

\[\begin{bmatrix} \dot{\boldsymbol{x}}\\ y \end{bmatrix} = \begin{bmatrix} A & \boldsymbol{b}\\ \boldsymbol{c}^T & d \end{bmatrix} \begin{bmatrix} \boldsymbol{x}\\ u \end{bmatrix} \]

特点

• 一阶常系数线性微分方程组
• \(A\)是一个方阵
• 其它暂时不了解

非线性系统的线性化

非线性系统

\[\left\{ \begin{aligned} \dot{\boldsymbol x}&=\boldsymbol f(\boldsymbol x, u)\\ y&=g(\boldsymbol x, u) \end{aligned} \right. \]

• 平衡点

  当输入\(u(t)=u_0\)时，\(\dot{\boldsymbol x}=\boldsymbol f(\boldsymbol x_0, u_0)\)，此时的\(\boldsymbol x\)处于平衡态。

• 向量导数的定义

  \[\frac{\partial g}{\partial \boldsymbol x^T}\triangleq \begin{bmatrix} \frac{\partial g}{\partial x_1} & \frac{\partial g}{\partial x_2}&\dots&\frac{\partial g}{\partial x_n} \end{bmatrix}\\ \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}^{T}} \triangleq\left[\begin{array}{c} \frac{\partial f_{1}}{\partial \boldsymbol{x}^{T}} \\ \frac{\partial f_{2}}{\partial \boldsymbol{x}^{T}} \\ \vdots \\ \frac{\partial f_{n}}{\partial \boldsymbol{x}^{T}} \end{array}\right]=\left[\begin{array}{cccc} \frac{\partial f_{1}}{\partial x_{1}} & \frac{\partial f_{1}}{\partial x_{2}} & \ldots & \frac{\partial f_{1}}{\partial x_{n}} \\ \frac{\partial f_{2}}{\partial x_{1}} & \frac{\partial f_{2}}{\partial x_{2}} & \ldots & \frac{\partial f_{2}}{\partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_{n}}{\partial x_{1}} & \frac{\partial f_{n}}{\partial x_{2}} & \ldots & \frac{\partial f_{n}}{\partial x_{n}} \end{array}\right] \]

• 线性化

  • 思想：在平衡点附近，用一阶近似代替非线性函数

  • 计算

    令\(\dot{\boldsymbol x}_\delta=\dot{\boldsymbol x}-\dot{\boldsymbol x}_0\)，\(u_\delta=u-u_0\)，则

    \[\begin{bmatrix} \dot{\boldsymbol{x}}_\delta\\ y_\delta \end{bmatrix} = \begin{bmatrix} A & \boldsymbol{b}\\ \boldsymbol{c}^T & d \end{bmatrix} \begin{bmatrix} \boldsymbol{x}_\delta\\ u_\delta \end{bmatrix} \]

    其中

    \[\begin{bmatrix} A & \boldsymbol{b}\\ \boldsymbol{c}^T & d \end{bmatrix} = \begin{bmatrix} \left.\frac{\partial \boldsymbol f}{\partial\boldsymbol{x}^{T}}\right|_{\boldsymbol x=\boldsymbol x_0\atop u=u_0} & \left.\frac{\partial \boldsymbol f}{\partial u}\right|_{\boldsymbol x=\boldsymbol x_0\atop u=u_0}\\ \left.\frac{\partial g}{\partial \boldsymbol{x}^{T}}\right|_{\boldsymbol x=\boldsymbol x_0\atop u=u_0} & \left.\frac{\partial g}{\partial u}\right|_{\boldsymbol x=\boldsymbol x_0\atop u=u_0} \end{bmatrix} \]

三种表示法的相互转换

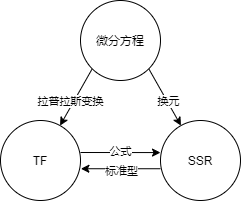
从微分方程到TF

• 回忆信号与系统，要注意前提是假设所有的初态都是0。
• 系统的单位冲激响应的拉普拉斯变换即是系统的TF。

从微分方程到SSR

见“简单了解状态空间表示”。

从SSR到TF（单入单出系统）

对SSR进行拉普拉斯变换得到

\[\left\{ \begin{aligned} s\tilde{\boldsymbol{x}}(x) &=A\tilde{\boldsymbol{x}}(s)+\boldsymbol{b} \tilde u(s) \\ \tilde y(s) &=\boldsymbol{c}^{T} \tilde{\boldsymbol{x}}(s)+d \tilde u(s) \end{aligned} \right. \]

消去\(\tilde{\boldsymbol x}(s)\)得到

\[\tilde y(s)=[\boldsymbol c^T(sI-A)^{-1}\boldsymbol b+d]\tilde u(s) \]

由系统的单位冲激响应的拉普拉斯变换即是系统的传递函数，得

\[G(s)=\boldsymbol c^T(sI-A)^{-1}\boldsymbol b+d=\frac{\boldsymbol c^T\mathrm{adj}(sI-A)^{-1}\boldsymbol b}{\mathrm{det}(sI-A)}+d \]

从TF到SSR（只记录了结论）

能控和能观标准型

n阶微分方程对应的TF待定系数最多有\(2n+2\)，而对应的SSR的待定系数有\(n^2+2n+1\)个，所以从TF到SSR不唯一，故定义了一些标准型。假设有TF如下：

\[G(s)=\frac{b_ns^n+{b}_{n-1} s^{n-1}+{b}_{n-2} s^{n-2}+\cdots+{b}_{1} s+{b}_{0}}{s^{n}+a_{n-1} s^{n-1}+\cdots+a_{1} s+a_{0}}=\frac{\hat{b}_{n-1} s^{n-1}+\hat{b}_{n-2} s^{n-2}+\cdots+\hat{b}_{1} s+\hat{b}_{0}}{s^{n}+a_{n-1} s^{n-1}+\cdots+a_{1} s+a_{0}}+b_{n} \]

其中\(\hat b_i=b_i-b_na_i\)。则对应的SSR矩阵如下：

	\(A\)	\(\boldsymbol b\)	\(\boldsymbol c\)	\(d\)
能控标准型	\(\begin{bmatrix}0 & 1 & 0 & \cdots & 0\\0 & 0 & 1 & \cdots & 0\\\vdots & \vdots & \vdots & \ddots & \vdots \\0 & 0 & 0 & \cdots & 1\\-a_0 & -a_1 & -a_2 &\cdots & -a_{n-1}\end{bmatrix}\)	\(\begin{bmatrix}0\\0\\\vdots\\0\\1\end{bmatrix}\)	\(\begin{bmatrix}\hat b_0\\\hat b_1\\\vdots\\\hat b_{n-2}\\\hat b_{n-1}\end{bmatrix}\)	\(b_n\)
能观标准型	\(\begin{bmatrix}0 & 0 & \cdots & 0 & -a_0\\1 & 0 & \cdots & 0 & -a_1\\0 & 1 & \cdots & 0 & -a_2\\\vdots & \vdots & \ddots & \vdots & \vdots \\0 & 0 & \cdots &1 & -a_{n-1}\end{bmatrix}\)	\(\begin{bmatrix}\hat b_0\\\hat b_1\\\vdots\\\hat b_{n-2}\\\hat b_{n-1}\end{bmatrix}\)	\(\begin{bmatrix}0\\0\\\vdots\\0\\1\end{bmatrix}\)	\(b_n\)

对角和约当标准型

对角标准型

如果有n个不同的极点，TF可改写为：

\[G(s)=b_n+\frac{c_1}{s-p_1}+\frac{c_2}{s-p_2}+\dots+\frac{c_n}{s-p_n} \]

其中\(c_i\)可由留数定理确定：\(c_i=\lim_\limits{s\to p_i}(s-p_i)G(s)\)。则SSR表示为

\[A =\begin{bmatrix}p_1 & 0 & \cdots & 0\\0 & p_2 & \cdots & 0\\\vdots & \vdots & \ddots & \vdots\\0 & 0 & \cdots & p_n\end{bmatrix},\quad\boldsymbol b=\begin{bmatrix}1\\1\\\vdots\\1\end{bmatrix},\quad\boldsymbol c=\begin{bmatrix}c_1\\c_2\\\vdots\\c_n\end{bmatrix},\quad d=b_n \]

约当标准型

如果有重极点，TF可改写为：

\[\begin{aligned} G(s)=& \frac{c_{1,1}}{\left(s-p_{1}\right)^{n_{1}}}+\frac{c_{1,2}}{\left(s-p_{1}\right)^{n_{1}-1}}+\cdots+\frac{c_{1, n_{1}}}{s-p_{1}} \\ &+\frac{c_{2,1}}{\left(s-p_{2}\right)^{n_{2}}}+\frac{c_{2,2}}{\left(s-p_{2}\right)^{n_{2}-1}}+\cdots+\frac{c_{2, n_{2}}}{s-p_{2}}+\cdots \\ &+\frac{c_{m, 1}}{\left(s-p_{m}\right)^{n_{m}}}+\frac{c_{m, 2}}{\left(s-p_{m}\right)^{n_{m}-1}}+\cdots+\frac{c_{m, n_{m}}}{s-p_{m}}+b_{n} \end{aligned} \]

其中\(c_{i,j}\)可由留数定理确定：\(c_{i,j}=\frac{1}{(j-1)!}\lim_\limits{s\to p_i}\frac{\mathrm{d}^{j-1}}{\mathrm{d}s^{j-1}}(s-p_i)^jG(s)\)。则SSR表示为

\[A =\begin{bmatrix}J_1 & 0 & \cdots & 0\\0 & J_2 & \cdots & 0\\\vdots & \vdots & \ddots & \vdots\\0 & 0 & \cdots & J_m\end{bmatrix},\quad\boldsymbol b=\begin{bmatrix}\boldsymbol b_1\\\boldsymbol b_2\\\vdots\\\boldsymbol b_m\end{bmatrix},\quad\boldsymbol c=\begin{bmatrix}\boldsymbol c_1\\\boldsymbol c_2\\\vdots\\\boldsymbol c_m\end{bmatrix},\quad d=b_n \]

其中

\[J_i= \begin{bmatrix} p_i & 1 & 0 & \cdots & 0 & 0\\ 0 & p_i & 1 & \cdots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & 0 & \cdots & 1 & 0\\ 0 & 0 & 0 & \cdots & p_i & 1\\ 0 & 0 & 0 & \cdots & 0 & p_i \end{bmatrix} ,\quad \boldsymbol b_i= \begin{bmatrix} 0\\ 0\\ \vdots\\ 0\\ 1 \end{bmatrix} ,\quad \boldsymbol c_i= \begin{bmatrix} c_{i,1}\\c_{i,2}\\\vdots\\c_{i,n_i} \end{bmatrix} \]

常见物理模型及其建模

电路	力学
电阻\(v(t)=Ri(t)\)	阻尼\(v(t)=\frac{1}{b}f(t)\)
电感\(v(t)=L\frac{{\rm d}i(t)}{{\rm d}t}\)	弹簧\(v(t)=\frac{1}{k}\frac{{\rm d}f(t)}{{\rm d}t}\)
电容\(i(t)=C\frac{{\rm d}v(t)}{{\rm d}t}\)	质量\(f(t)=m\frac{{\rm d}v(t)}{{\rm d}t}\)

框图和信号流图

• 框图化简

  • 并联：\(\boldsymbol G=\boldsymbol G_1+\boldsymbol G_2\)

  • 串联：\(\boldsymbol G=\boldsymbol G_2\boldsymbol G_1\)（\(G_2\)连在\(G_1\)之后）

  • 反馈：\(\boldsymbol G_c=\frac{\boldsymbol G}{1+\boldsymbol G\boldsymbol H}\)（负反馈为+，正反馈则要改成-）

  • 移动求和点：\(\tilde{\boldsymbol{y}}=\boldsymbol{G} \tilde{\boldsymbol{r}}+\tilde{\boldsymbol{d}}=\boldsymbol{G}\left(\tilde{\boldsymbol{r}}+\boldsymbol{G}^{-1} \tilde{\boldsymbol{d}}\right)\)

    

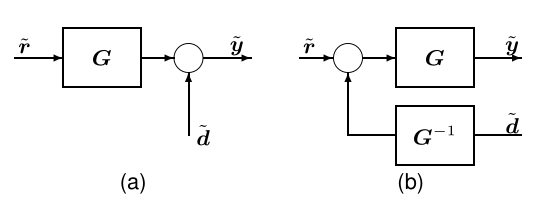
  • 移动分支点：添加\(\boldsymbol G\)或者\(\boldsymbol G^{-1}\)

• 信号流图的梅森公式：一种通过流程化的将信号流图转换为TF的方法，计算相对麻烦。

  

  • 注意“removed“是节点也要去一起去掉。

标签：02,frac,数学模型,boldsymbol,end,bmatrix,partial,动态,vdots
来源： https://www.cnblogs.com/harold-lu/p/15390612.html