Harris 特征点 从线性代数基础开始详细分析
作者:互联网
Harris 特征点 从线性代数基础开始详细分析
Harris特征点是图像处理中很基础和常见的寻找特征码的一个方法,由于涉及到很多数学知识,导致数学学得不好的我在网上看资料很吃力,零零碎碎看了一下午总算看了给眉头,总结起来以后忘了复习,也给广大数学苦手的小伙伴一点指引
1.角点
角点可以看作是各个方向变化很剧烈的点,一般来说,这些点附近的内容就构成了图像的特征(我觉得人脑应该也是通过识别这些特征点来记忆和认识事物的),数学上可以说是各个方向梯度很大的点吧。有各种各样的方法来寻找角点,Harris是其中一种。注意角点和边缘的区别,边缘是在某一方向上的线状边缘。

2.检测方法
检测角点一般会使用一个固定大小的窗口,通过窗口(有点像核矩阵)在图像上移动前后的差别是否足够大来判断。
假设图像是I(x,y), 移动量是ux和uy, 窗口是w(x,y),那么检测以下值的大小就能判断是不是角点
E
(
u
,
v
)
=
Σ
w
(
x
,
y
)
[
I
(
x
+
u
,
y
+
v
)
−
I
(
x
,
y
)
]
2
E(u,v)=\Sigma w(x,y)[I(x+u,y+v)-I(x,y)]^2
E(u,v)=Σw(x,y)[I(x+u,y+v)−I(x,y)]2
然而实际上Harris不是直接使用了这个E,主要是希望能找到一个更精简干练的定义,所以将这个算式继续深入分析。
窗口w(x,y)
w(x,y)一般是正态分布的权重矩阵,因为中心是我们最关心的嘛,周边的稍次。当然最简单的0,1也行。这里用0,1来做,这样后面的计算就方便解释了
E
(
u
,
v
)
=
Σ
[
I
(
x
+
u
,
y
+
v
)
−
I
(
x
,
y
)
]
2
E(u,v)=\Sigma [I(x+u,y+v)-I(x,y)]^2
E(u,v)=Σ[I(x+u,y+v)−I(x,y)]2

移动前后平方差 和[I(x+u,y+v)-I(x,y)]^2
这个项用泰勒展开,再矩阵化一下。
泰勒展开不知道的搜一下,这里只需要用到最简单的,就是个二元微积分
E
(
u
,
v
)
=
Σ
[
I
(
x
+
u
,
y
+
v
)
−
I
(
x
,
y
)
]
2
=
Σ
[
I
(
x
,
y
)
+
u
I
x
+
v
I
y
−
I
(
x
,
y
)
]
2
=
Σ
[
u
2
I
x
2
+
v
2
I
y
2
+
2
u
v
I
x
I
y
]
E(u,v)=\Sigma [I(x+u,y+v)-I(x,y)]^2 =\Sigma [I(x,y)+ uI{x} +vI{y}-I(x,y)]^2 =\Sigma [u^2Ix^2 +v^2Iy^2 +2uvIxIy]
E(u,v)=Σ[I(x+u,y+v)−I(x,y)]2=Σ[I(x,y)+uIx+vIy−I(x,y)]2=Σ[u2Ix2+v2Iy2+2uvIxIy]
Σ [ u 2 I x 2 + v 2 I y 2 + 2 u v I x I y ] = Σ [ u v ] [ I x 2 I x I y I x I y I y 2 ] [ u v ] = [ u v ] Σ [ I x 2 I x I y I x I y I y 2 ] [ u v ] \Sigma [u^2Ix^2 +v^2Iy^2 +2uvIxIy]= \Sigma \left[ \begin{matrix} u & v \end{matrix} \right] \left[ \begin{matrix} Ix^2 & IxIy \\ IxIy & Iy^2\\ \end{matrix} \right] \left[ \begin{matrix} u \\ v\\ \end{matrix} \right]= \left[ \begin{matrix} u & v \end{matrix} \right] \Sigma \left[ \begin{matrix} Ix^2 & IxIy \\ IxIy & Iy^2\\ \end{matrix} \right] \left[ \begin{matrix} u \\ v\\ \end{matrix} \right] Σ[u2Ix2+v2Iy2+2uvIxIy]=Σ[uv][Ix2IxIyIxIyIy2][uv]=[uv]Σ[Ix2IxIyIxIyIy2][uv]
取
M
=
Σ
[
I
x
2
I
x
I
y
I
x
I
y
I
y
2
]
M= \Sigma \left[ \begin{matrix} Ix^2 & IxIy \\ IxIy & Iy^2\\ \end{matrix} \right]
M=Σ[Ix2IxIyIxIyIy2]
所以
E
(
u
,
v
)
=
[
u
v
]
M
[
u
v
]
E(u,v) =\left[ \begin{matrix} u & v \end{matrix} \right] M \left[ \begin{matrix} u \\ v\\ \end{matrix} \right]
E(u,v)=[uv]M[uv]
注意M是对称矩阵,而且E(u,v)是一个二次型
什么是二次型
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-95vKowCl-1633182760755)(https://raw.githubusercontent.com/spicyoil/markdown_rep/main/Harris%20%E7%89%B9%E5%BE%81%E7%82%B9%20%20%E4%BB%8E%E7%BA%BF%E6%80%A7%E4%BB%A3%E6%95%B0%E5%9F%BA%E7%A1%80%E5%BC%80%E5%A7%8B%E8%AF%A6%E7%BB%86%E5%88%86%E6%9E%90/image-20211002211146404.png)]
简单来说就是齐次二次函数吧,这里只考虑2元,这时函数一定能表现为以下形式
f
(
x
,
y
)
=
[
x
y
]
[
a
b
c
d
]
[
x
y
]
f(x,y)= \left[ \begin{matrix} x & y \end{matrix} \right] \left[ \begin{matrix} a & b \\ c & d\\ \end{matrix} \right] \left[ \begin{matrix} x\\ y\\ \end{matrix} \right]
f(x,y)=[xy][acbd][xy]
二次型能干嘛呢,二次型可以很方便的用图形的方式来表现函数在各个方向上大小范围,而这正好适合是我们用来判断是否是角点的重点
比如如果E(u,v)是下图的函数,那么可以说45°方向的变化比较大,是吧(但这里还不好说是不是角点)
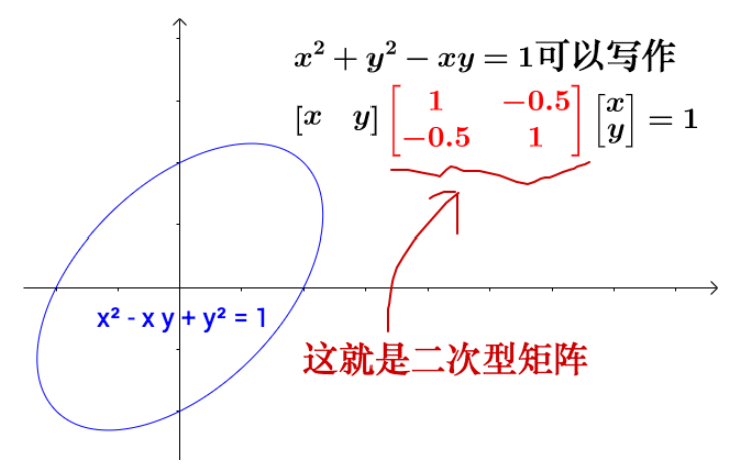
接着我们分解矩阵
[
1
−
0.5
−
0.5
1
]
=
[
−
2
/
2
2
/
2
2
/
2
−
2
/
2
]
[
1.5
0
0
0.5
]
[
−
2
/
2
2
/
2
2
/
2
−
2
/
2
]
\left[ \begin{matrix} 1 & -0.5 \\ -0.5 & 1\\ \end{matrix} \right] = \left[ \begin{matrix} -\sqrt2/2 & \sqrt2/2 \\ \sqrt2/2 & -\sqrt2/2\\ \end{matrix} \right] \left[ \begin{matrix} 1.5 & 0 \\ 0 & 0.5\\ \end{matrix} \right] \left[ \begin{matrix} -\sqrt2/2 & \sqrt2/2 \\ \sqrt2/2 & -\sqrt2/2\\ \end{matrix} \right]
[1−0.5−0.51]=[−2
/22
/22
/2−2
/2][1.5000.5][−2
/22
/22
/2−2
/2]
前后两矩阵是旋转矩阵,不影响大小。中间是拉伸,影响大小。
注意看,分解矩阵实际上做的是矩阵的对角化。大家去看看矩阵对角化的资料就会知道,最后对角化的矩阵(就是负责拉伸的矩阵)的各个值就是原矩阵的特征值~,所以特征值就成为了是否是角点的判断量
回到Harris方法这
说了这么多,再看看实际例子。拿以下的3个种类做例子,分别是边缘,平坦,和角点。

如果你试着去计算他们的E(u,v),就会是下图的感觉,种类不同各个像素的集中或者分散的特征就不同

再把散点给圈起来(圈成椭圆或者圆形),外圈是不是就像二次型的图形啦。是的,我们就是要拟合成2次型。
注意这个例子里Corner和LineraEdge的Iy,Ix都是正数,但我们能够猜想到也会有正负,负负的情况,所以圈圆时是将四个象限都考虑着圈的哈。

为什么要拟合成二次型呢?不用再说了吧,就是向用特征值来判断角点。

通过上图中特征值的关系就能判断了,不过Harris继续构造了一个变量,通过一个变量来衡量
R
=
λ
1
∗
λ
2
−
k
(
λ
1
+
λ
2
)
R= \lambda1*\lambda2 - k(\lambda1+\lambda2)
R=λ1∗λ2−k(λ1+λ2)
其中k是参数,需要调试。
最后设定R的阈值,我们就能检测角点了。
标签:begin,right,end,matrix,角点,Harris,线性代数,详细分析,left 来源: https://blog.csdn.net/zhuyanjun0818/article/details/120589461