港队系列算法、数据结构
作者:互联网
- 写在前面
这两个东西其实并没有什么联系,但是因为都是由 @dd_d 首创的,所以写在一起。
Update:不想新开博客了,所以以后 dd_d 有什么新发明就直接在这里更新了。
-
港队线段树
这是一种高效且简便好写的优秀线段树( 由香港队长发明的 ),拥有良好的均摊复杂度。
在同时需要记录多个标记时,有十分简洁的下传方式,甚至无需标记( 与标记永久化类似思想,但不完全相同 )。
实现原理则是充分利用了线段树叶子节点的性质,使其能快速合并信息。
其实港队线段树不难理解,如果你学过线段树,看代码就能完全理解,但是从古至今却只有他一个人想到了这种高妙的办法。
大致算法流程( 用修改举例,其他同理 )
void update(...) {
if(The length of the section is only 1) {
//Edit the value
...
return ;
}
//push_down(...);
if(Can reach the left section) update(The left son);
if(Can reach the right section) update(The right son);
}
当遇到实际题目时,如果能充分利用叶子节点的性质,一些情况下可以使码量大大减小,对港队来说 push_down 只是画蛇添足!
- 举个例子:[清华集训2012]序列操作
按照题解思路将式子展开以后,其他操作可以直接套用港队线段树。
询问只需要按照推出来的式子,预处理一下组合数,从叶子向上乘起来即可,式子不写了,可以去题解区看,会比好写很多,且变得完全没有思维难度了。
- 有同学可能会问:为什么复杂度是对的呢?
考虑当询问一定会分为多个区间,参考下图
这些区间上的存储值合并后就是答案。
考虑这些区间的长度有长有短,在询问随机情况下,我们也许只要 \(1\) 个就能获得答案,也许 \(\log(n)\) 次就会获得答案。
仔细推理一下或感性理解一下就能发现,均摊复杂度为单次 \(O(\log n)\)。
至于修改操作,在较好的随机情况下是 \(O(\sqrt{n})\) 级别的,不算很劣,如果仔细的研究数据规模后,可以在比较好条件下达到 \(O(\log(n))\) 甚至 \(O(1)\)。
但是在方便的前提下谁会在意复杂度呢
-
马表
这个目前还在理论阶段,没有比较优秀的实践价值。
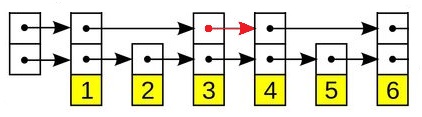
马表,即为带修 st 表,最基础的马表支持期望 \(O(\log n)\) 单点修改,\(O(k)\) 求区间 RMQ,\(k\) 为一个常数,一般的马表 \(k\) 期望为 \(4\sim5\),优秀的可达到 \(2.64\) 左右大小。
思路就是借用一个 Skip List 的分层概念,修改会在表上多开一个节点,节点过多就重复利用,使节点数控制在一定范围内,查询就在每层上查询。
可以参考图片理解,红色箭头表示一次修改。
相比线段树,马表就有很大优化空间,修改时一些点可以只先在高层打标记,询问时下传到下层,实测所用时间比线段树的 \(\frac{1}{2}\) 还略快。
并且 st 表能维护的内容马表都能维护,并且可以可持久化,十分优秀。
-
ex马表
带修带插入的马表,在马表基础上再倍增分块,插入在最顶层,查询再向下新建,小块暴力修改,过大后暴力 split。
但是 \(k\) 能被卡的非常大,可以搞一个估价函数,为块数在再乘一个指数函数,通常取 \((\sqrt{2})^x\),超过一定之后层与层之间 shuffle 一下,再重建层与层之间的边,在随机数据下跑的飞快。
先考虑插入的每个数字大小和位置都是随机的,即随机到每一块的概率是 \(O(\log n)\) 的,也就是说,期望 \(O(\log^2 n)\) 次会有 \(\frac{\log_2 n}{\log_k n}\) 次 split( \(k\) 是期望层数 ),因此 split 的总复杂度为 \(O(\frac{q}{\log_k n})\),不会对马表总复杂度产生影响。
然后是重构,由 split 平衡后,至少要 \(\log n\times tn\) 次才会重构,\(t\) 取决于估价函数的优劣,大概是 \(0.23\sim0.61\)。总复杂度为\(\frac{q}{\log n\times tn}\times n\log n\),为 \(O(\frac{q}{t})\),上限约为 \(O(4.236\times q)\),同样小于朴素马表。
做法似乎十分暴力,但复杂度同样正确。
删除也可以按照这个思路,块内少了就 merge,不平衡就重构,复杂度同理。
ex马表也同马表一样,st 表能维护的都能维护。
- 马表的其他用处
马表可用范围很广,能套用其他数据结构,可以在马表上倍增,或是用马表优化建图,但由于还是理论数据结构,这里就不展开了。
-
港队矩乘
首先考虑原来矩阵乘法的式子:
\[\begin{bmatrix} a_{1,1}&\cdots&a_{1,k}\\ \vdots&\ddots&\vdots\\ a_{n,1}&\cdots&a_{n,k}\\ \end{bmatrix} \times \begin{bmatrix} b_{1,1}&\cdots&b_{1,m}\\ \vdots&\ddots&\vdots\\ b_{k,1}&\cdots&b_{k,m}\\ \end{bmatrix} = \begin{bmatrix} c_{1,1}&\cdots&c_{1,m}\\ \vdots&\ddots&\vdots\\ c_{n,1}&\cdots&c_{n,m}\\ \end{bmatrix} \]先对于每个数考虑它对最终矩阵的贡献,例如 \(a\) 中一个数,它就会对 \(c\) 中同一行的数产生贡献。
因此可以枚举 \(a\) 中每个数,这个贡献就为 \(a_{i,j}\times\begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\) 再加到 \(\begin{bmatrix}c_{i,1}&\cdots&c_{i,m}\end{bmatrix}\) 上。
这里大家可能很疑惑,这不就是矩阵乘法换了个形式表达吗,不能说十分相似,只能说一模一样。
接下来就是港队的操作时间了,考虑怎么将计算过程简化,因为 \(a,b\) 贡献不独立,想想有没有奇怪的打 tag 方法。定义新运算 \(\begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\boxtimes a_{i,j}\),先不管这个式子实际意义,但是从形式上可通过原式可以发现:
\[\begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\boxtimes x + \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\boxtimes y = \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\boxtimes (x\boxplus y) \]同样你可能也会看着这个式子很疑惑,这不就是矩阵乘常数吗,不能说十分相似,只能说一模一样。
现在不考虑把算出来的值往 \(c\) 里拍,而是直接通过这种新运算把 \(c\) 表示出来,这个 \(\cup\) 表示把每个行矩阵依次拼成一个矩阵。
\[\bigcup_{j=1}^{k} \left( \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} \boxtimes \left( \boxplus_{i=1}^{n} a_{i,j} \right) \right) \]现在考虑如果每个运算时间复杂度为 \(\mathcal{O}(1)\) 的话,这个式子已经做到 \(\mathcal{O}(n^2)\),但是事实却不是这样,\(\boxtimes\) 是 \(\mathcal{O}(n)\)
你可能也会看着这堆操作很疑惑,这不就是原矩乘的问题吗,不能说十分相似,只能说一模一样。
但是这种描述方式就能做出一些变形,例如这样:
\[\bigcup_{j\in \mathbb{S}} \boxtimes_{p_i} \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} , p_i\in \mathbb{P} \]仅仅求这个式子的复杂度和质数分布就已经是呈线性关系的了,也就是说,我们最多只能在复杂度上乘 \(\frac{1}{\log n}\),并且这个 \(\mathbb{S}\) 甚至只能枚举,变劣了吗?真的吗?
考虑去找 \(p_i\) 对应的 \(\mathbb{S}\)
\[\begin{aligned} \mathbf{Original} &= \bigcup_{j\in \mathbb{S}} \left( \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} \boxtimes p_i \right) \\ &= \left( \bigcup_{j\in \mathbb{S}} \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} \right) \boxtimes p_i \\ &= \left( \overline{\bigcup_{j\not\in \mathbb{S}}} \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} \right) \boxtimes p_i \\ \end{aligned} \]\[\begin{aligned} \mathbf{\sum Original} &= \sum \begin{bmatrix} b_{1,1}&\cdots&b_{1,m}\\ \vdots&\ddots&\vdots\\ b_{t\in\mathbb{S},1}=0&\cdots&b_{t\in\mathbb{S},1}=0\\ \vdots&\ddots&\vdots\\ b_{k,1}&\cdots&b_{k,m}\\ \end{bmatrix} \boxtimes p_i \\ &= \sum_{i=1}^{|\mathbb{P}\cup[x\le V]|} (-1)^i \left( \begin{bmatrix} b_{1,1}&\cdots&b_{1,m}\\ \vdots&\ddots&\vdots\\ b_{t\in\mathbb{S},1}=0&\cdots&b_{t\in\mathbb{S},1}=0\\ \vdots&\ddots&\vdots\\ b_{k,1}&\cdots&b_{k,m}\\ \end{bmatrix} \boxtimes \left( \gcd\limits_{j\in \mathbb{S},|\mathbb{S}|\le i}^j p_j \right) \right) \\ &= \sum_{i=1}^{|\mathbb{P}\cup[x\le V]|} (-1)^i \begin{bmatrix} b_{1,1}\boxplus G&\cdots&b_{1,m}\boxplus G\\ \vdots&\ddots&\vdots\\ b_{t\in\mathbb{S},1}=0&\cdots&b_{t\in\mathbb{S},1}=0\\ \vdots&\ddots&\vdots\\ b_{k,1}\boxplus G&\cdots&b_{k,m}\boxplus G\\ \end{bmatrix} , G=\gcd\limits_{j\in \mathbb{S},|\mathbb{S}|\le i}^jp_j \\ &= \sum_{i1=1}^{n} \sum_{j1=1}^{n} \sum_{i2=1}^{n} \sum_{j2=1}^{n} \begin{bmatrix} b_{1,1}\boxplus g(D)&\cdots&b_{1,m}\boxplus g(D)\\ \vdots&\ddots&\vdots\\ b_{k,1}\boxplus g(D)&\cdots&b_{k,m}\boxplus g(D)\\ \end{bmatrix} , g(x)=\prod\limits_{i\in\mathbb{P},i|x}i,D=\gcd(a_{i1,j1},a_{i2,j2}) \\ &= \sum_{i=1}^{cnt} \begin{bmatrix} b_{1,1}\boxplus g(D)&\cdots&b_{1,m}\boxplus g(D)\\ \vdots&\ddots&\vdots\\ b_{n,1}\boxplus g(D)&\cdots&b_{n,m}\boxplus g(D)\\ \end{bmatrix} \\ &= \sum_{i=1}^{cnt} \begin{bmatrix} b_{1,1}\boxplus g(B)&\cdots&b_{1,m}\boxplus g(D)\\ \vdots&\ddots&\vdots\\ b_{n,1}\boxplus g(D)&\cdots&b_{n,m}\boxplus g(D)\\ \end{bmatrix} \end{aligned} \]懒了,就把后面的所有有用的推导都放这了。
第一部分感觉上非常无用,又将式子变回去了,但这个打 tag 方式从行矩阵扩展到矩阵,就能用于解决这个根本问题了。
全集的价值可以直接算出来,子集 \(\mathbb{S}\) 可以通过每个 \(p_i\) 建一个链表快速求出。
由于 \(\sum\limits_{x\in\mathbb{P}}^{x\le n} \frac{1}{x} = \ln(\ln n) + \mathcal{O}(1)\)(为方便后面就写作 \(\log V\) 了),求 \(S\) 部分复杂度 \(\mathcal{O}(n\log^2 V)\),其余计算部分复杂度为 \(\mathcal{O}(n^2\log V)\)。
但是真的解决了吗?真的吗?你觉得呢?
实际上很好发现复杂度瓶颈在求 \(p_i\),只能做到 \(\mathcal{O}(V)\),原式也非积性函数。
后面几步推导就完全解决了这个问题,通过 \(\gcd\) 的转化,就不需要直接求 \(p_i\) 了,还能优化一定常数。
但是要注意一个点,就是新定义运算的原意义是打 tag,是不同于简单的加或乘的,不然理解其中几步的推导可能会出现偏差。
处理掉不存在的行,然后可以通过预处理区间 \(\gcd\) 优化了求答案过程。
dd_d 现在万事缠身,没有造什么题,不过可以自己去找一些 dp 转成矩乘用这个方法优化试试。
- 特别鸣谢 @Freedom_King 的帮助和支持。
标签:mathbb,begin,end,cdots,港队,算法,bmatrix,数据结构,vdots 来源: https://www.cnblogs.com/jur-cai/p/16596771.html