卷积和反卷积详细说明
作者:互联网
转载:https://zhuanlan.zhihu.com/p/124626648
转载:https://www.cnblogs.com/wanghui-garcia/p/10791328.html
1. 卷积 Convolution
1.1 卷积输出尺寸
输出图像尺寸可以根据以下公式获得
:输入图像尺寸
: padding 大小
: 卷积核大小
: 步长

卷积:蓝色的输入图片(4 x4),深蓝色代表卷积核(3 x 3),绿色为输出图像(2 x 2)
假如现在有一个4 x 4的图片, 使用一个3 x 3的kernel 进行卷积
图片: 卷积核:
strides = 1 , padding = 0, 卷积后,输出图像的尺寸为
如果卷积核很大,那么可以使用傅里叶变换, 提升卷积的性能。
2. 反卷积 Transposed Convolution
由于卷积核一般比原始图像小,所以卷积之后的图像尺寸往往会变小。有时候我们需要将卷积后的图像还原成原始图像的尺寸,即实现图像从小分辨率到大分辨率的映射,这种操作就叫做上采样(Upsampling)。而反卷积正是一种上采样方法。
反卷积,又称为转置卷积(Transposed Convolution,),它是一种特殊的卷积,先padding来扩大图像尺寸,紧接着跟正向卷积一样,旋转卷积核180度,再进行卷积计算。看上去就像,已知正向卷积的输出图像,卷积核,得到正向卷积中的原始图像(并非真的得到原始图像,像素点是不一样的,但是尺寸是一致的)。
它看上去像是正向卷积的逆运算,但其实并不是。因为反卷积只能还原原始图像的尺寸,但是并不能真的恢复原始图像内容,即每个元素值其实是不一样的。
卷积过程中:
表示输出,
表示输入,
:表示kernel的大小,
:表示padding,
: 表达strides
反卷积过程中:
表示输出,
表示输入,
:表示kernel的大小,
:表示padding,
: 表达strides
卷积后的 则反卷积的
, 一般卷积核是不会变的,
,需要注意的是,卷积与反卷积的padding很可能是不一样。
2.1 Striding
反卷积的Striding跟卷积有点不一样,它在输入的每个元素之间插入 个值为0的元素
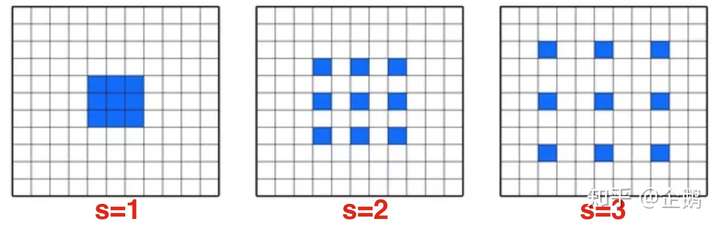
Transposed convolution : Striding
如果我们将反卷积看成是一种特殊的卷积,它其实是根据反卷积中指定的步长strides, 修改了输入 , 根据strding 进行补0操作,得到
, 其大小变为
, 然后对
进行s=1的卷积。例如,对应上面的三个子图,
对应的
,
对应的
,
对应的
。
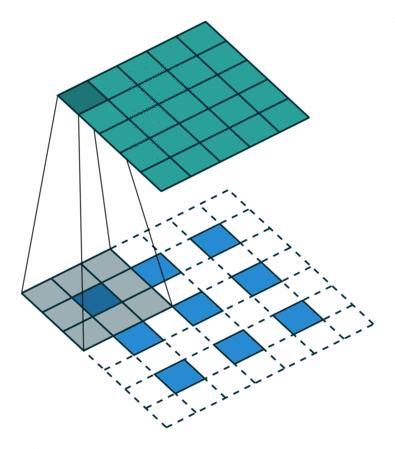
反卷积:蓝色是输入(3 x 3), 灰色是卷积核(3 x 3), 绿色是输出(5 x 5),padding=1,strides = 2
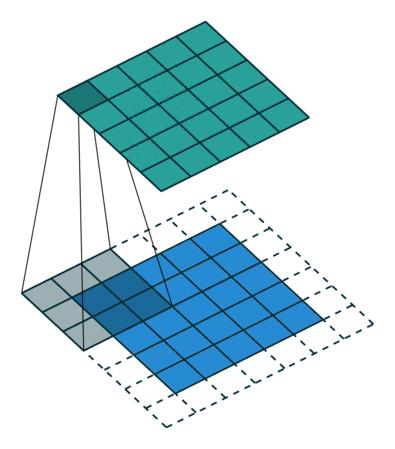
反卷积:蓝色是输入(5 x 5), 灰色是卷积核(3 x 3), 绿色是输出(5 x 5),padding=1,strides =1
3 反卷积的输出尺寸

可见这里没考虑output_padding
output_padding的作用:可见nn.ConvTranspose2d的参数output_padding的作用.
论文 A guide to convolution arithmetic for deep learning 涉及了14种有关反卷积的尺寸大小公式的关系,但是归纳起来就只有两种情况。
3.1
反卷积的输出尺寸为 或者
对应上面提到的卷积的例子,分别用上面两条公式进行验算,验算结果都成立。
卷积时, ,
,
,
, 所以计算的结果
反卷积, ,
,
,
,
代入第一个式子
代入第二个式子
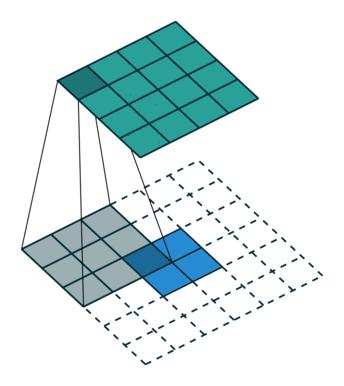
反卷积,蓝色是输入(2 x 2), 灰色是卷积核(3 x 3), 绿色是输出(4 x 4),padding=2
4.下面举例说明
https://github.com/vdumoulin/conv_arithmetic#convolution-arithmetic
1)当stride=1时,就不会进行插值操作,只会进行padding,举例说明:
卷积操作为:
蓝色为输入特征图Hin*Hin=4*4,绿色为输出特征图Hout*Hout=2*2,卷积核kernel_size=3, stride=1
根据式子Hout = floor( Hin + 2*padding - kernel_size / stride) + 1
可得padding=0

其对应的逆卷积操作为:
蓝色为输入特征图Hout*Hout=2*2,绿色为输出特征图Hin*Hin=4*4,卷积核kernel_size=3, stride=1
卷积时的padding=0
将这些值代入上面的式子Hin = (Hout - 1) * stride - 2*padding + kernel_size
果然输入Hout*Hout=2*2能得到输出Hin*Hin=4*4
变形过程为:
paddingnew = kernel_size - padding -1 = 3 -0 -1 = 2
所以可见下方的蓝色最后的大小为7*7 = Hout + 2*paddingnew = 2 + 2*2 = 6

⚠️这里可见是有padding的,为什么定义是为no padding呢?
这是因为它对应的卷积操作的padding=0
1)当stride=2时,进行插值和padding操作,举例说明:
卷积操作为:
蓝色为输入特征图Hin*Hin=5*5,绿色为输出特征图Hout*Hout=3*3,卷积核kernel_size=3, stride=2
根据式子Hout = floor( Hin + 2*padding - kernel_size / stride) + 1
可得padding=1

其对应的逆卷积操作为:
蓝色为输入特征图Hout*Hout=3*3,绿色为输出特征图Hin*Hin=5*5,卷积核kernel_size=3,stride=2
卷积时的padding=1
将这些值代入上面的式子Hin = (Hout - 1) * stride - 2*padding + kernel_size
果然输入Hout*Hout=3*3能得到输出Hin*Hin=5*5
变形操作为:
Hout_new = Hout + (stride-1) * (Hout-1) = 3 + (2-1)*(3-1) = 5
paddingnew = kernel_size - padding -1 = 3 -1 -1 = 1
所以可见下方的蓝色最后的大小为7*7 = Hout_new + 2*paddingnew = 5 + 2*1 = 7

⚠️因为这里的逆卷积对应的卷积操作的padding= 1,所以这里不是no padding,而是padding
标签:Hout,padding,kernel,卷积,说明,stride,详细,Hin 来源: https://www.cnblogs.com/hansjorn/p/14767592.html