Codeforces 1458E - Nim Shortcuts(博弈论+BIT)
作者:互联网
首先看到这样的题我们不妨从最特殊的情况入手,再逐渐推广到一般的情况。考虑如果没有特殊点的情况,我们将每个可能的局面看作一个点 \((a,b)\) 并映射到坐标系上。考虑按照博弈论的套路求出每个点是必胜点还是必输点,就这题而言,显然一个点 \((x,y)\) 是必胜点当且仅当 \(\exists z<x\) 满足 \((z,y)\) 是必胜点或者 \(\exists z<y\) 满足 \((y,z)\) 是必胜点。打个表 即可知道一个状态 \((x,y)\) 为 P 态(必输点)当且仅当 \(x=y\),否则该状态为 N 态(必胜点)。这个异常好理解,如果 \(x=y\) 那不论先手取了多少石子,后手都可以在另一堆中取相同数量的棋子,最终肯定会留给先手一个 \((0,0)\) 的局面。
紧接着我们考虑有一个特殊点的情况,我们假设这个特殊点为 \((x,y)\),那么可以分出三种情况:
-
\(x=y\),那么这个点本来就是 P 态,显然不会对每个点的 N/P 态产生任何影响
-
\(x>y\),如图所示,假设该点为 \(P\),那么该点在直线 \(y=x\) 的右下方。显然该点不会对该点左边及下方的点的状态产生影响,也就是说产生直接影响的只可能是 \(P\) 沿 \(+x\) 方向引出的射线(图中的黄色射线)或沿 \(+y\) 方向引出的射线(图中的橙色射线),将这些点全都变成 N 态。而显然黄色射线上的所有点本来就是 N 态,橙色射线上的点除了其与 \(y=x\) 的交点其他也都是 N 态,故这个点产生的效果是将橙色射线与 \(y=x\) 的交点 \((x,x)\) 变为 N 态,但这样会带来一个副作用,那就是 \((x,x)\) 变为 N 态了,\((x+1,x)\) 反而无法直接到达 N 态的点,变成 P 态了,按照类似的方式归纳也可知道这样会导致 \((x+2,x+1),(x+3,x+2),\cdots,(k+1,k)\) 变为 P 态,即图中的红色部分为 P 态,其余为 N 态。

-
\(x<y\),与 \(x<y\) 的情况类似,只不过变成 \((y,y)\) 变为 N 态,\((y,y+1),(y+1,y+2),\cdots\) 变为 P 态。
\(n\le 1\) 的情况已经解决了,那么怎样解决原题呢?
注意到题目有个显然的性质就是每行每列中除特殊点外最多一个 P 点,也就是说每列除特殊点外的 P 点组成的函数是一个分段函数,并且每段都是一个形如 \(y=x+k\) 的函数,比方说下图:
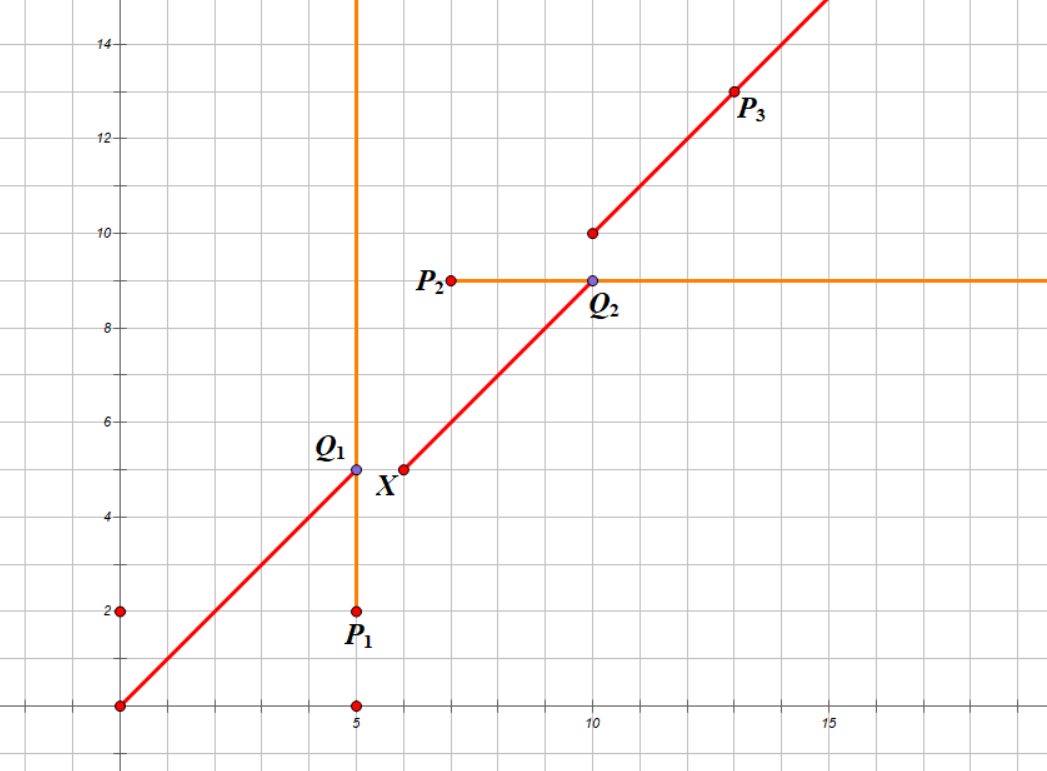
我们考虑重新观察一下上面每个关键点的作用效果。对于每个向上引出射线的关键点(例如图中的 \(P_1\)),我们可以近似地看作删除了该关键点所在的列并将左右两部分重新拼在一起,对于每个向右引出射线的关键点我们也可近似地看作删除了该关键点所在的行,这样一来思路就来了,我们将所有关键点按横坐标从小到大排序,对于一个关键点 \((x,y)\),我们记 \(s\) 为 \(x\) 前面有多少列被删除,\(t\) 为 \(y\) 前面有多少行被删除,那么该关键点所在部分 P 态的点的函数表达式就是 \(y=x+s-t\),我们按照线性规划的思想将这个点与这条线的关系进行比较,如果 \(y<x+s-t\) 那么该点应当向上引出射线,即删除这一列,那么我们只需令 \(s\) 加一,注意如果这一列已经删除了就不用再删了。如果 \(y=x+s-t\) 那么该点可以直接忽略,如果 \(y>x+s-t\) 那么应当删除这一行。最后考虑回答每个询问,首先特判掉待询问点与某个关键点重合的情况,此时答案显然为 LOSE,其次如果存在某个关键点与待询问点同行同列,那么答案显然是 WIN,否则我们还是求出 \(s\) 表示 \(x\) 前面有多少列被删除,\(t\) 表示 \(y\) 前面有多少行被删除,并检验 \((x,y)\) 是否在 \(y=x+s-t\) 上即可。求 \(t\) 可以采用离散化+树状数组。
时间复杂度 \(n\log n\)。
const int MAXN=1e5;
int n,m;
struct event{
int x,y,id;
bool operator <(const event &rhs) const{
if(x!=rhs.x) return x<rhs.x;
else if(y!=rhs.y) return y<rhs.y;
return id<rhs.id;
}
} a[MAXN*2+5];
int key[MAXN*2+5],uni[MAXN*2+5],cnt=0,num=0;
int get(int x){return lower_bound(uni+1,uni+num+1,x)-uni;}
bool is[MAXN*2+5],ans[MAXN+5];int c1=0,lst=0;
int t[MAXN*2+5];
void add(int x){for(int i=x;i<=num;i+=(i&-i)) t[i]++;};
int query(int x){int ret=0;for(int i=x;i;i&=(i-1)) ret+=t[i];return ret;}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y),key[++cnt]=a[i].y;
for(int i=1;i<=m;i++) scanf("%d%d",&a[i+n].x,&a[i+n].y),a[i+n].id=i,key[++cnt]=a[i+n].y;
sort(a+1,a+n+m+1);sort(key+1,key+cnt+1);key[0]=-1;
for(int i=1;i<=cnt;i++) if(key[i]!=key[i-1]) uni[++num]=key[i];
for(int i=1;i<=n+m;i++){
int pos=get(a[i].y);
if(a[i].id){
if(a[i-1].x==a[i].x&&a[i-1].y==a[i].y) ans[a[i].id]=1;
else if(a[i].x!=lst&&!is[pos]){
int dif=query(pos)-c1;
// printf("%d\n",dif);
if(a[i].y==a[i].x+dif) ans[a[i].id]=1;
}
} else {
int dif=query(pos)-c1;
if(a[i].x+dif<a[i].y){//up
if(!is[pos]) add(pos),is[pos]=1;
} else if(a[i].x+dif>a[i].y){//down
if(lst!=a[i].x) lst=a[i].x,c1++;
}
}
}
for(int i=1;i<=m;i++) printf("%s\n",(ans[i])?"LOSE":"WIN");
return 0;
}
标签:每个,删除,Nim,1458E,Codeforces,射线,int,该点,关键点 来源: https://www.cnblogs.com/ET2006/p/Codeforces-1458E.html