其他分享
首页 > 其他分享> > 2021-02-08

2021-02-08

作者：互联网

电机学2——变压器（上）

电机学2——变压器（上）

网课学习网址：mooc

变压器的基本原理和结构

变压器的基本原理和分类

image-20210202103919503

1、基本工作原理

·以磁场为媒介，通过电磁感应作用，把一种电压的交流电转换为相同频率的另一种电压的交流电

·一个铁心，两个绕组

·两个绕组只有磁耦合，没有电联系image-20210202120058469

&要点：只有通交流电才能工作；两个绕组匝数不同，电压就不同

2、变压器的分类

按绕组个数按相数按用途按冷却方式
自耦变压器单相变压器升压变压器油浸自冷
双绕组变压器三相变压器降压变压器干式空气自冷
三绕组变压器多相变压器隔离变压器油浸风冷
油浸水冷

&最常用的变压器：单相双绕组降压变压器

变压器的基本结构

1、磁路部分——铁心（core）

·电工钢片迭压而成闭合磁路

·冷轧电工钢片，片之间涂敷绝缘漆（为了减少损耗）

·常用的形状有：E、C、U

image-20210202152840068

2、电路部分——绕组（winding）

·用的是绝缘线包，线圈；单相变压器：两个

==·原端线圈：==接到电源上；首尾符合AX；一次线圈

==·副端线圈：==接到负载上；首尾符号ax；二次线圈

3、结构分类

image-20210202154456521

&变压器的表示方法：

image-20210202154608367

变压器的额定值（铭牌值）

·是指使用变压器时，必须满足的一些条件，如电压

·最主要的：额定容量；额定电压；额定电流；联接组号

1、额定容量 S N S_N SN​（注意是容量capacity）

—是视在功率，就是电压*电流

—因为变压器的效率很高，所有我们认为原副端的视在功率相等

—定价的依据

image-20210202161359507

2、额定电压 U N U_N UN​（rated voltage）

原方：外加的额定电源电压 U 1 N U_{1N} U1N​

副方：原方额定时负载端的空载电压 U 2 N U_{2N} U2N​（即电势）

——三相时为线电压

——对电器使用中，额定电压最重要

3、额定电流 I N I_N IN​

——由 S N S_N SN​、 U N U_N UN​求得

——单相时： S N = U N I N S_N=U_NI_N SN​=UN​IN​

——三相时： S N = 3 U N I N S_N=\sqrt{3}U_NI_N SN​=3 ​UN​IN​

——三相时为线电流

4、联接组号

三相所特有的

5、其他额定参数（相数、频率、温升、冷却等）

&attention：

·额定电压对电器最重要！否则会烧毁设备！

·各国电源标准不同：注意尺寸大小转换；注意接线形式转换

变压器分析的两个基础

理想变压器

1、变压器的运行过程

image-20210202173313739

2、无用的因素

·铜损-原因：有电流，磁阻有电阻

·铁损-原因：有磁通，铁心有磁阻

·漏磁-原因：有磁通，耦合度不够

&主磁通和漏磁通的区别：

(1)、作用不同：

主磁通传递能量，交链原副方

漏磁通只消耗磁势，只起磁压降的作用

(2)、特性不同

主磁通和电流呈非线性关系（介质是铁心）

漏磁通和电流呈线性关系（介质是空气）

3、理想变压器的条件

无铜损——绕组电阻为0

无铁损——铁心磁阻为0，即磁导无穷大

无漏磁通——耦合系数为1，或者漏磁系数为0

&思考问题：

问题1：哪个条件最难实现？无漏磁最难实现

问题2：理想变压器干啥用？理解变压器的物理本质，用于定性分析

正方向原则

·只有定出来正方向，才能列电压平衡方程式

一般采用电动机惯例，认为变压器对电源是个电动机，无源的（passive）

·主要原则：

电压方向 → \rightarrow →电流方向

电流方向 → \rightarrow →磁通方向（右手）

磁通方向 → \rightarrow →电势方向（右手）

安培定则（Right hand grip rule）是表示电流和电流激发磁场的磁感线方向间关系的定则，又称右手螺旋定则。

通电直导线中的安培定则（安培定则一）：用右手握住通电直导线，让大拇指指向电流的方向，那么四指的指向就是磁感线的环绕方向；

通电螺线管中的安培定则（安培定则二）：用右手握住通电螺线管，让四指指向电流的方向，那么大拇指所指的那一端是通电螺线管的N极。

image-20210202182226598

image-20210202182251694

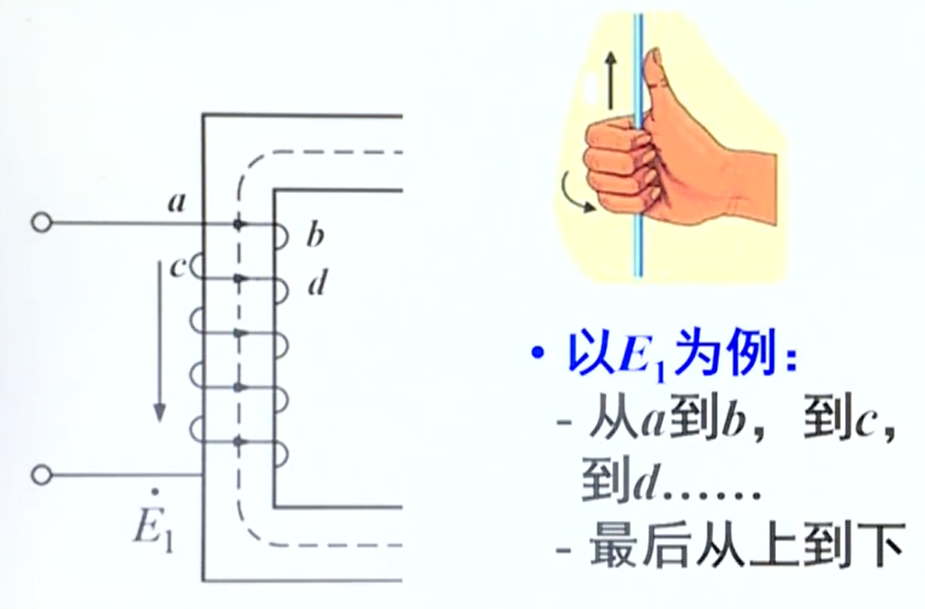
image-20210202182858490

image-20210202182940995

&思考问题:

问题1: U 1 U_1 U1​和 E 1 E_1 E1​反方向了，对不对？电势是反电势，没问题

问题2: E 2 E_2 E2​和 I 2 I_2 I2​同方向了，对不对？ E 2 E_2 E2​对副端来讲是副端所有能量的来源，所以是先有 E 2 E_2 E2​后有 I 2 I_2 I2​

image-20210202183938840

&从本质上讲：原端绕组对电源来讲是负载；副端绕组对另个负载来讲是电源。

但是！！为了整个变压器能够列出电压平衡方程式，我们采取了同样的标准对原副方进行规定

变压器空载运行时的方程式

空载运行过程

1、变压器的空载运行过程

·变压器空载：副线圈不接负载，开路

·电路方程式 Σ e = Σ u \Sigma e=\Sigma u Σe=Σu，即所有的电势升=所有电压降

image-20210202194616209

image-20210202214650104

2、空载电流 I 0 I_0 I0​

空载运行时原方绕组中流过的电流

·大小 I 0 I_0 I0​=（2~10%） I N I_N IN​，空载不太费电

·波形 电压为正弦波时电流为尖顶波。==问题：为什么？==待补充

·相位 近似与主磁通同相，超前一个 α \alpha α（很小）角，“铁损角“

·垂直分解 与 Φ \Phi Φ同相的磁化电流 I u ˙ \dot{I_u} Iu​˙​；超前 Φ 9 0 o \Phi 90^o Φ90o的铁损分量 I F e ˙ \dot{I_{Fe}} IFe​˙​

I 0 ˙ = I F e ˙ + I u ˙ \dot{I_0}=\dot{I_{Fe}}+\dot{I_u} I0​˙​=IFe​˙​+Iu​˙​

问题1：铁损角的物理意义是什么？待补充

问题2：为什么是超前不是滞后？参考第四节等效电路中的相量图

image-20210202222859338

3、主电动势 E 1 E_1 E1​
所 有 的 电 势 ： { e 1 = − N 1 d Φ d t （ 原 端 电 势 ） e 2 = − N 2 d Φ d t （ 副 端 电 势 ） e 1 σ = − N 1 d Φ 1 σ d t （ 原 端 漏 电 势 ） 所有的电势：\left\{ \begin{aligned} e_1=-N_1\frac{d\Phi}{dt}（原端电势）\\ e_2=-N_2\frac{d\Phi}{dt}（副端电势）\\ e_{1\sigma}=-N_1\frac{d\Phi_{1\sigma}}{dt}（原端漏电势）\\ \end{aligned} \right. 所有的电势：⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧​e1​=−N1​dtdΦ​（原端电势）e2​=−N2​dtdΦ​（副端电势）e1σ​=−N1​dtdΦ1σ​​（原端漏电势）​
·假定认为主磁通按正弦规律变化

image-20210203103844557

·主电势的大小和方向

有效值： E 1 = E 1 m / 2 = 4.44 f 1 N 1 Φ m E_1=E_{1m}/\sqrt{2}=4.44f_1N_1\Phi_m E1​=E1m​/2 ​=4.44f1​N1​Φm​

相量： E ˙ 1 = − j 4.44 f 1 N 1 Φ ˙ m \dot E_1=-j4.44f_1N_1\dot\Phi_m E˙1​=−j4.44f1​N1​Φ˙m​（注意负号！主磁通是峰值！）

方向：滞后于主磁通 9 0 o 90^o 90o

同理，副边主电势 E ˙ 2 = − j 4.44 f 1 N 2 Φ ˙ m \dot E_2=-j4.44f_1N_2\dot\Phi_m E˙2​=−j4.44f1​N2​Φ˙m​

image-20210203104413062

4、原边漏抗电势

image-20210203105448581

&注： N d Φ = d Ψ Nd\Phi=d\Psi NdΦ=dΨ L 1 σ L_{1\sigma} L1σ​漏电感，与匝数平方成正比，与漏磁导成正比

磁通链 Ψ \Psi Ψ就是磁通量 Φ \Phi Φ乘以与磁通线相关的线圈的匝数 N N N。

·若励磁电流按正弦规律变化

同上推导得

image-20210203111421075

重要结论1：

原方绕组的漏电抗表征的是漏磁通对电流的关系，与匝数和几何尺寸有关，对一个做好了的变压器，是定值，不变的！

5、电势与变比

U 1 N ≈ E 1 U_{1N}\approx E_1 U1N​≈E1​（原端电压与原端的主电势近似相等）

U 2 N ≈ E 2 U_{2N}\approx E_2 U2N​≈E2​（副端的额定电压与副端的电势（即空载电压）相等）
U 1 N U 2 N ≈ E 1 E 2 = 4.44 N 1 f 1 Φ m 4.44 N 2 f 1 Φ m = N 1 N 2 = k \frac{U_{1N}}{U_{2N}}\approx\frac{E_1}{E_2}=\frac{4.44N_1f_1\Phi_m}{4.44N_2f_1\Phi_m}=\frac{N_1}{N_2}=k U2N​U1N​​≈E2​E1​​=4.44N2​f1​Φm​4.44N1​f1​Φm​​=N2​N1​​=k
k k k就是变比，匝数之比

重要结论2：

只要两边匝数不同，对应的电压就不同，就能变压

变压器的电压平衡方程式

image-20210203114410368

其中 Z 1 = r 1 + j x 1 Z_1=r_1+jx_1 Z1​=r1​+jx1​，称为远端绕组的（阻 漏抗），或者说是漏阻抗

r 1 r_1 r1​：原端绕组电阻

x 1 x_1 x1​：原端绕组漏电抗

&注：数值大小上漏阻抗压降比较小，所以电压主要是在和电势相平衡
U ˙ 1 ≈ − E ˙ 1 U 1 ≈ E 1 = 4.44 f 1 N 1 Φ m \dot U_1\approx-\dot E_1\\ U_1\approx E_1=4.44f_1N_1\Phi_m U˙1​≈−E˙1​U1​≈E1​=4.44f1​N1​Φm​
重要结论3：

变压器主磁通主要取决于端电压、频率和匝数，与负载大小基本无关！会稍有变化；“恒磁通”概念

变压器空载运行时的等效电路

等效电路

U ˙ 1 = ( − E ˙ 1 ) + I ˙ 0 Z 1 \dot U_1=(-\dot E_1)+\dot I_0Z_1 U˙1​=(−E˙1​)+I˙0​Z1​

定义 ( − E ˙ 1 ) (-\dot E_1) (−E˙1​)是一个由 I 0 I_0 I0​引起的压降，分析最简单

令 − E ˙ 1 = I ˙ 0 Z m = I ˙ 0 ( r m + j x m ) -\dot E_1=\dot I_0Z_m=\dot I_0(r_m+jx_m) −E˙1​=I˙0​Zm​=I˙0​(rm​+jxm​)

Z m Z_m Zm​：变压器的励磁阻抗

r m r_m rm​：变压器的励磁电阻

x m x_m xm​：变压器的励磁电抗

带入得：等效结果 U ˙ 1 = I ˙ 0 ( Z 1 + Z m ) \dot U_1=\dot I_0(Z_1+Z_m) U˙1​=I˙0​(Z1​+Zm​)

image-20210204122020495

&物理意义： x m x_m xm​反映的是主电抗，大电感； r m r_m rm​反映的是铁损（注意和绕组电阻 r 1 r_1 r1​铜损的区别）

问题： x m x_m xm​和 r m r_m rm​谁大谁小？待补充

相量图

· Φ ˙ m \dot\Phi_m Φ˙m​作为参考相量， E 1 E_1 E1​落后 9 0 o 90^o 90o，再画出 − E 1 -E_1 −E1​

·等值正弦空载电流超前主磁通一个铁损角 α \alpha α

电流为什么是超前主磁通的？

image-20210204124722720
数值上：
P F e = ( − E ˙ 1 ) I ˙ 0 = I 0 2 r m = ( − E ˙ 1 ) ( I ˙ F e + I ˙ u ) = ( − E ˙ 1 ) I ˙ F e = E 1 I F e P_{Fe}=(-\dot E_1)\dot I_0=I_0^2r_m\\ =(-\dot E_1)(\dot I_{Fe}+\dot I_u)\\ =(-\dot E_1)\dot I_{Fe}=E_1I_{Fe} PFe​=(−E˙1​)I˙0​=I02​rm​=(−E˙1​)(I˙Fe​+I˙u​)=(−E˙1​)I˙Fe​=E1​IFe​
由公式得： − E 1 -E_1 −E1​和 I 0 I_0 I0​的相位角差一定小于90度； − E 1 -E_1 −E1​和 I F e I_{Fe} IFe​一定是同相的！

标签：02,电势,08,变压器,2021,电压,绕组,磁通,dot
来源： https://blog.csdn.net/weixin_47852662/article/details/113760358