密度最大值聚类-MDCA
作者:互联网
1 引言
2014年6月,Alex Rodriguez和Alessandro Laio在ScienceScience上发表了一篇名为《Clustering by fast search and find of density peaks》的文章,提供了一种简洁而优美的聚类算法,是一种基于密度的聚类方法,可以识别各种形状的类簇,并且参数很容易确定。它克服了DBSCAN中不同类的密度差别大、邻域范围难以设定的问题,鲁棒性强。
在文章中提出的聚类方法DPCA算法(Desity Peaks Clustering Algorithm)基于这样一种假设:对于一个数据集,聚类中心被一些低局部密度的数据点包围,而且这些低局部密度点距离其他有高局部密度的点的距离都比较大。
5.2 若干概念
- 局部密度ρiρi的定义为: ρi=∑jχ(dij−dc)ρi=∑jχ(dij−dc) 其中, χ(x)={1 if x<00 if otherwiseχ(x)={1 if x<00 if otherwise 其中dcdc是一个截断距离,ρiρi即到对象ii的距离小于dcdc的对象的个数。由于该算法只对ρiρi的相对值敏感,所以对dcdc的选择是比较稳健的。
- 高局部密度点距离δiδi,其定义为:
δi=minj:ρj>ρi(dij)δi=minj:ρj>ρi(dij)
即在局部密度高于对象ii的所有对象中,到对象ii最近的距离。
而极端地,对于密度最大的那个对象,我们设置δ=max(dij)δ=max(dij);
只有那些密度是局部或者全局最大的点才会有远大于正常值的高局部密度点距离。
5.3 聚类过程
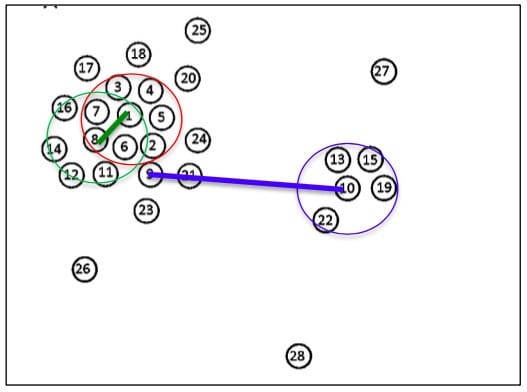
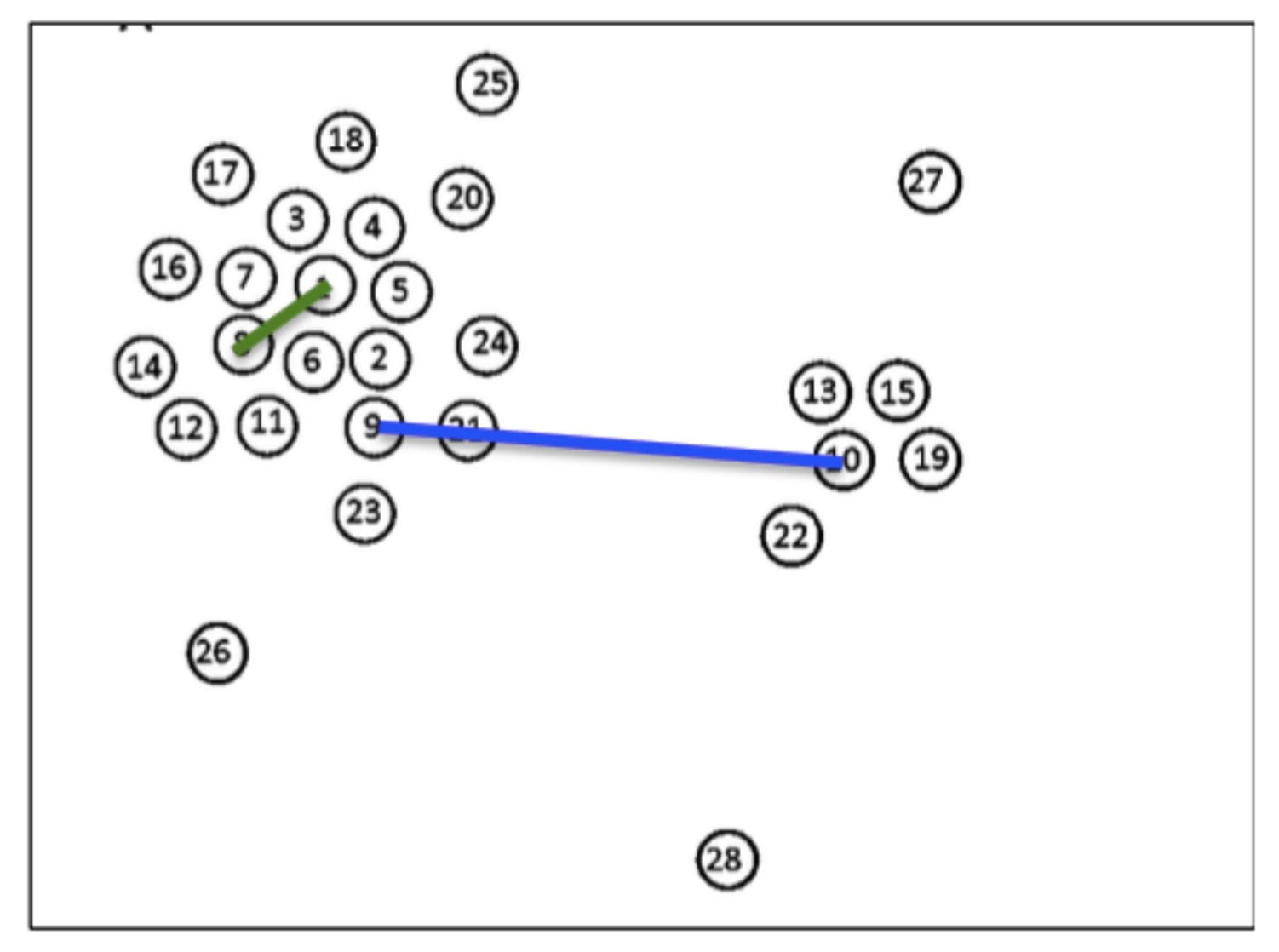
这个聚类实例摘自作者的PPT讲演,在一个二维空间中对数据进行聚类,具体步骤如下:
- 3、对每一个点,绘制出局部密度与高局部密度点距离的关系散点图
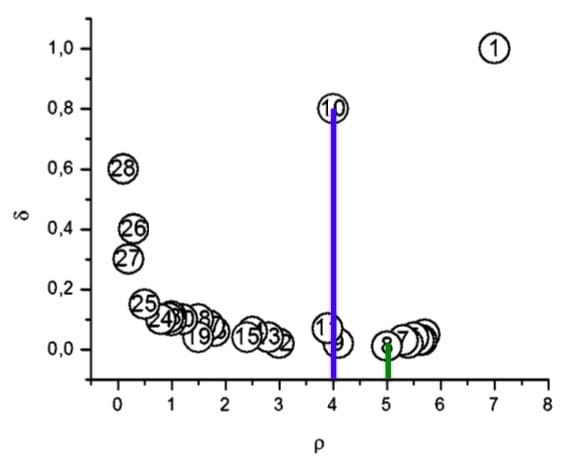
- 4、图上的异常点即为簇中心。如图所示,1和10两点的局部密度和高局部密度距离都很大,将其作为簇中心。
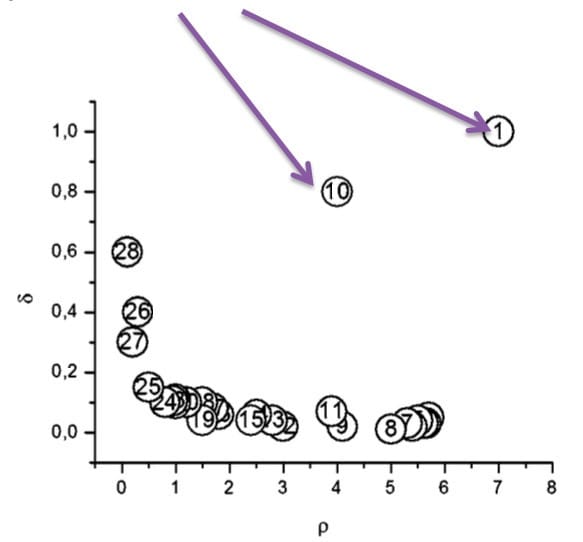
- 5、将其他的点分配给距离其最近的有着更高的局部密度的簇。(Assign each point to the same cluster of its nearest neighbor of higher density)
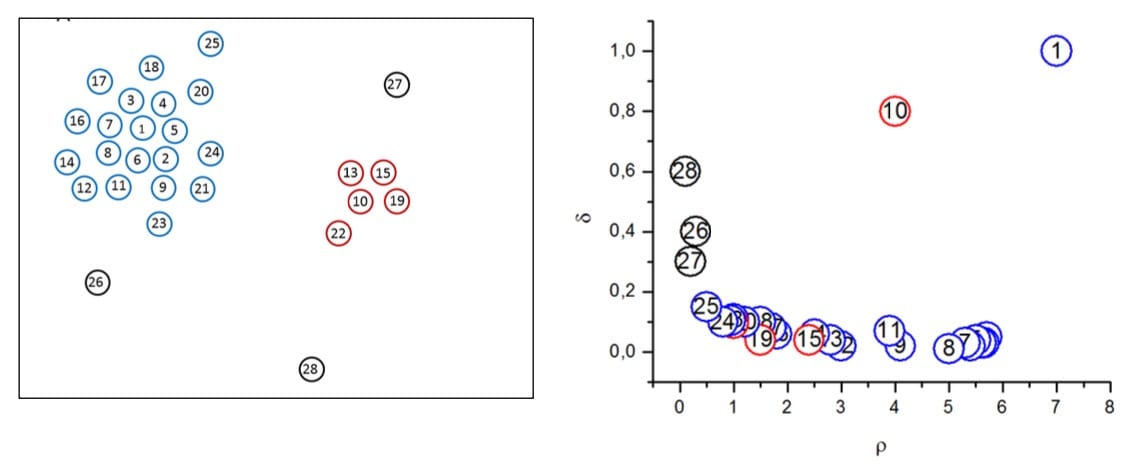
左图是所有点在二维空间的分布,右图是以ρρ为横坐标,以δδ为纵坐标绘制的决策图。容易发现,1和10两个点的ρiρi和δiδi都比较大,作为簇的中心点。26、27、28三个点的δδ也比较大,但是ρ比较小ρ比较小,所以是异常点。
5.4 一些关键点
-
簇中心的识别
- 那些有着比较大的局部密度ρiρi和很大的高局部密度δiδi的点被认为是簇的中心;
而高局部密度距离δiδi较大但局部密度ρiρi较小的点是异常点;
确定簇中心之后,其他点按照距离已知簇的中心最近进行分类,也可以按照密度可达的方法进行分类。
但是,这里我们在确定聚类中心时,没有定量地分析,而是通过肉眼观察,包含很多的主观因素。在上图中可以分明地用肉眼判断聚类中心,但是有些情况下无法用肉眼来判断。不过,对于那些在决策图中无法用肉眼判断出聚类中心的情形,作者在文中给出了一种确定聚类中心个数的提醒:计算一个将ρρ值和δδ值综合考虑的量 γi=ρiδiγi=ρiδi 显然γγ值越大,越有可能是聚类中心。因此,只需对其降序排列,然后从前往后截取若干个数据点作为聚类中心就可以了。
我们把排序后的γγ在坐标平面(下标为横轴,γγ值为纵轴)画出来,由图可见,非聚类中心的gammagamma值比较平滑,而从非聚类中心过渡到聚类中心时γγ有一个明显的跳跃,这个跳跃用肉眼或数值检测应该可以判断出来。作者在文末还提到,对于人工随机生成的数据集,γγ的分布还满足幂次定律,即logγlogγ,且斜率依赖于数据维度。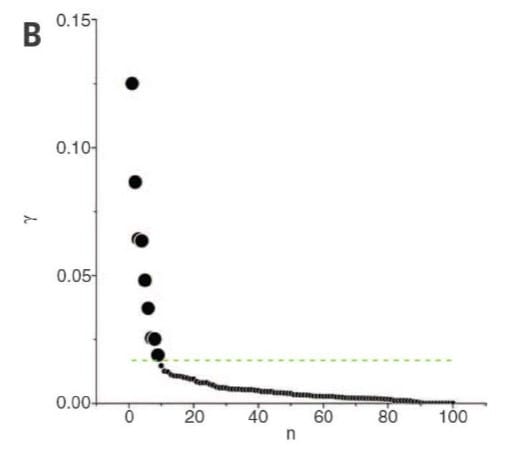
- 那些有着比较大的局部密度ρiρi和很大的高局部密度δiδi的点被认为是簇的中心;
-
截断距离dcdc的选择
- 一种推荐做法是选择dcdc,使得平均每个点的邻居数为所有点的1%~2%。参数dcdc的选取,从某种意义上决定这聚类算法的成败,取得太大或者太小都不行:如果取得太大,将使得每个数据点的ρρ值都很大以致区分度不高,极端情况是取dc>dmaxdc>dmax,则所有的数据点都归属于一个Cluster了;如果dcdc取得太小,同一个Cluster中就可能被拆分成多个,极端情况是dc<dmindc<dmin,则每个数据点都单独称为一个Cluster。作者将比例锁定在数据量的1%~2%,也是基于肉感数据集的经验值。
-
选定簇中心之后
- 在聚类分析中, 通常需要确定每个点划分给某个类簇的可靠性. 在该算法中, 可以首先为每个类簇定义一个边界区域(border region), 亦即划分给该类簇但是距离其他类簇的点的距离小于dcdc的点(这个区域由这样的数据点构成:它们本身属于该Cluster,但在与其距离不超过dcdc的范围内,存在属于其他Cluster的数据点). 然后为每个类簇找到其边界区域的局部密度最大的点, 令其局部密度为ρhρh. 该类簇中所有局部密度大于ρhρh的点被认为是类簇核心的一部分(亦即将该点划分给该类簇的可靠性很大), 其余的点被认为是该类簇的光晕(halo), 亦即可以认为是噪音. 图例如下
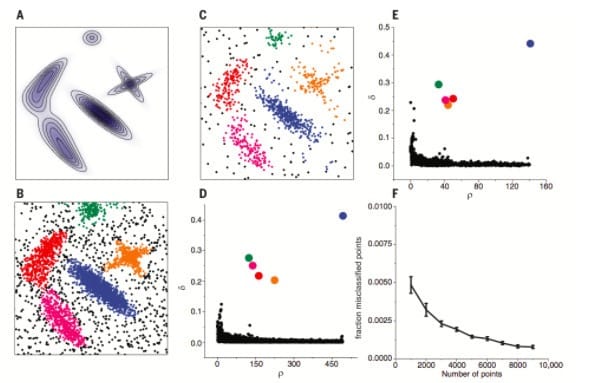
A图为生成数据的概率分布,B、C二图为分别从该分布中生成了4000,1000个点。D,E分别是B,C两组数据的决策图(decision tree),可以看到两组数据都只有五个点有比较大的ρiρi和很大的δiδi,这些点作为类簇的中心,在确定了类簇的中心之后,每个点被划分到各个类簇(彩色点),或者划分到类簇光晕(黑色点),F图展示的是随着抽样点数量的增多,聚类的错误率在逐渐下降,说明该算法是鲁棒的。
- 在聚类分析中, 通常需要确定每个点划分给某个类簇的可靠性. 在该算法中, 可以首先为每个类簇定义一个边界区域(border region), 亦即划分给该类簇但是距离其他类簇的点的距离小于dcdc的点(这个区域由这样的数据点构成:它们本身属于该Cluster,但在与其距离不超过dcdc的范围内,存在属于其他Cluster的数据点). 然后为每个类簇找到其边界区域的局部密度最大的点, 令其局部密度为ρhρh. 该类簇中所有局部密度大于ρhρh的点被认为是类簇核心的一部分(亦即将该点划分给该类簇的可靠性很大), 其余的点被认为是该类簇的光晕(halo), 亦即可以认为是噪音. 图例如下
标签:dij,中心,最大值,距离,密度,聚类,MDCA,局部 来源: https://www.cnblogs.com/ai-ldj/p/14301019.html