数据降维之等度量映射

数据降维含义

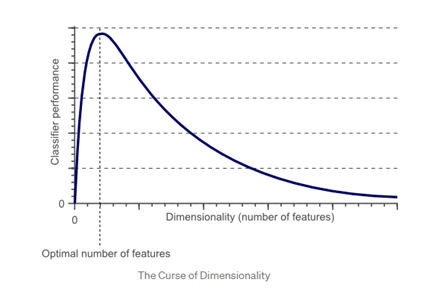
含义：数据降维的基本出发点是在尽量保留原始数据特征的前提下，降低参与建模的维度数。在降维过程中，无论未被表现出来的特征是噪音还是正常分布，这部分信息都无法参与建模。如果某些场景下需要所有数据集的完整特征，那么通常不选择降维。

数据降维好处

1 避免过度拟合

2 减少误导性数据，提高模型准确性

3 减少数据，算法训练更快

4 数据减少，节约存储空间

5 消除多余的特征和噪音

 

 

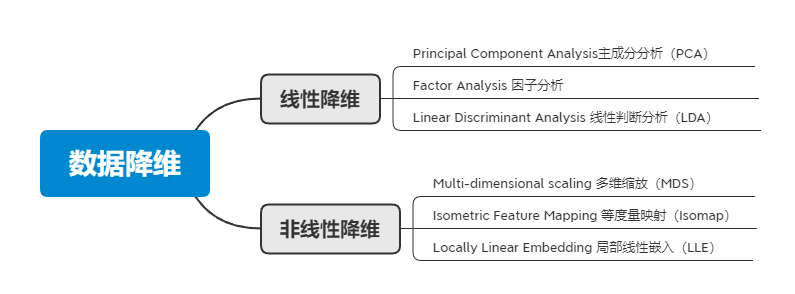
数据降维分类

 

等度量映射

流形学习

传统的机器学习方法中，数据点和数据点之间的距离和映射函数都是定义在欧式空间中的，然而在实际情况中，这些数据点可能不是分布在欧式空间中的，因此传统欧式空间的度量难以用于真实世界的非线性数据，从而需要对数据的分布引入新的假设。流形学习假设所处理的数据点分布在嵌入于外维欧式空间的一个潜在的流形体上，或者说这些数据点可以构成这样一个潜在的流形体。

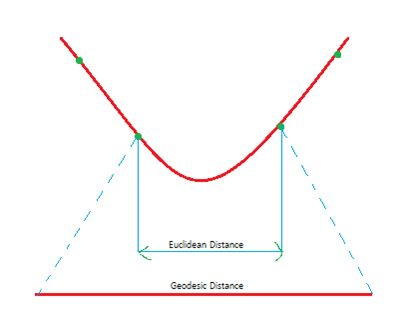
在三维空间中流行体上点与点之间的距离不能使用传统的欧式空间的距离来计算，而应该用测地线距离代表这两个点的实际距离。蓝色虚线为两个点的欧式距离，蓝色实线为两个点的测地线距离。但是测地线距离也不好测量，因此我们采用另一种路径近似代表测地线距离。

Euclidean Distance:欧式距离

Geodesic Distance: 测地线距离

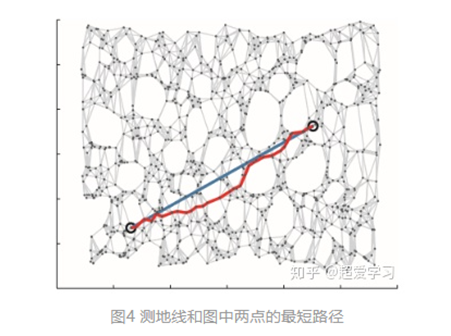
我们构建一个连通图，其中每个点只和距离这个点最近的k个点直接连接，和其他的点不直接连接。这样我们可以构建邻接矩阵，进而求出图中任意两个点的最短路径，代替测地线距离。蓝色线代表两个点之间的测地线距离，红色线代表图中两点的最短路径，两者距离相近，因此我们使用后者替代前者。

 

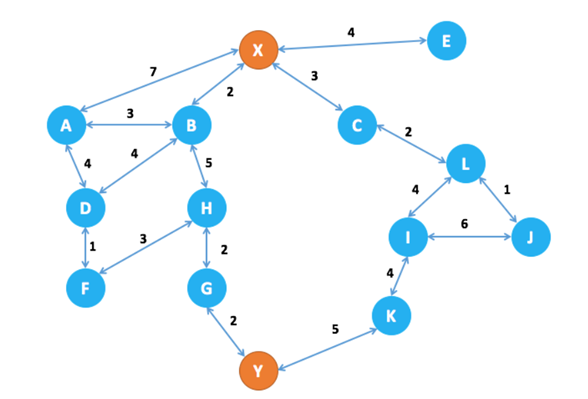
最短路径

使用Djikstra算法寻找X到Y的最短路径

X-> B-> H-> G-> Y

什么时候使用Isomap？

Isomap is better than linear methods when dealing with almost all types of real image and motion tracking

 

算法流程:

 

测试用例1

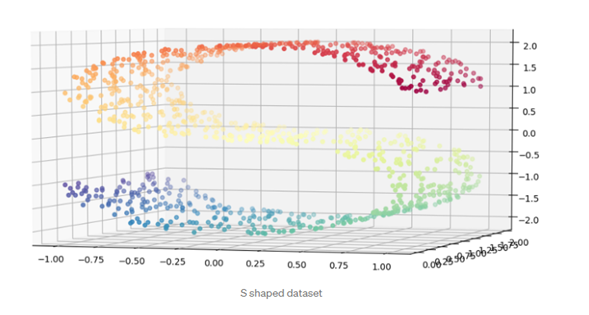
1 加载数据集，并且可视化显示

 

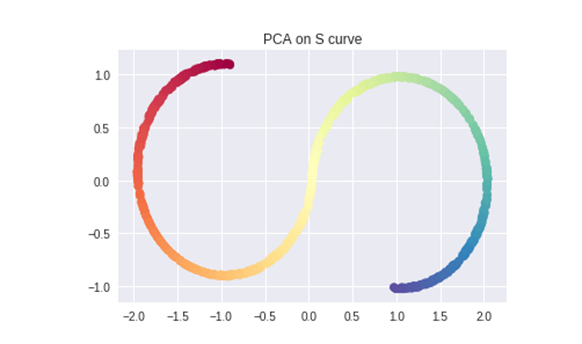
2 调用PCA算法

 

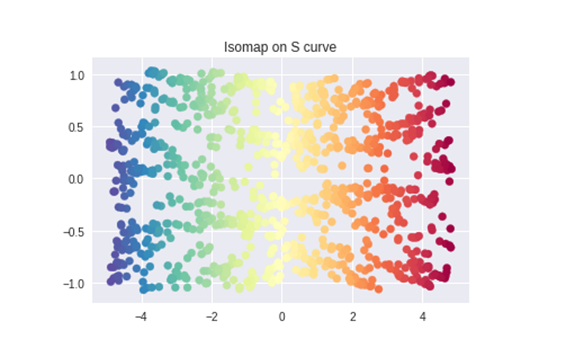
3 调用Isomap算法

 

测试用例2(人脸识别数据集)

 

 

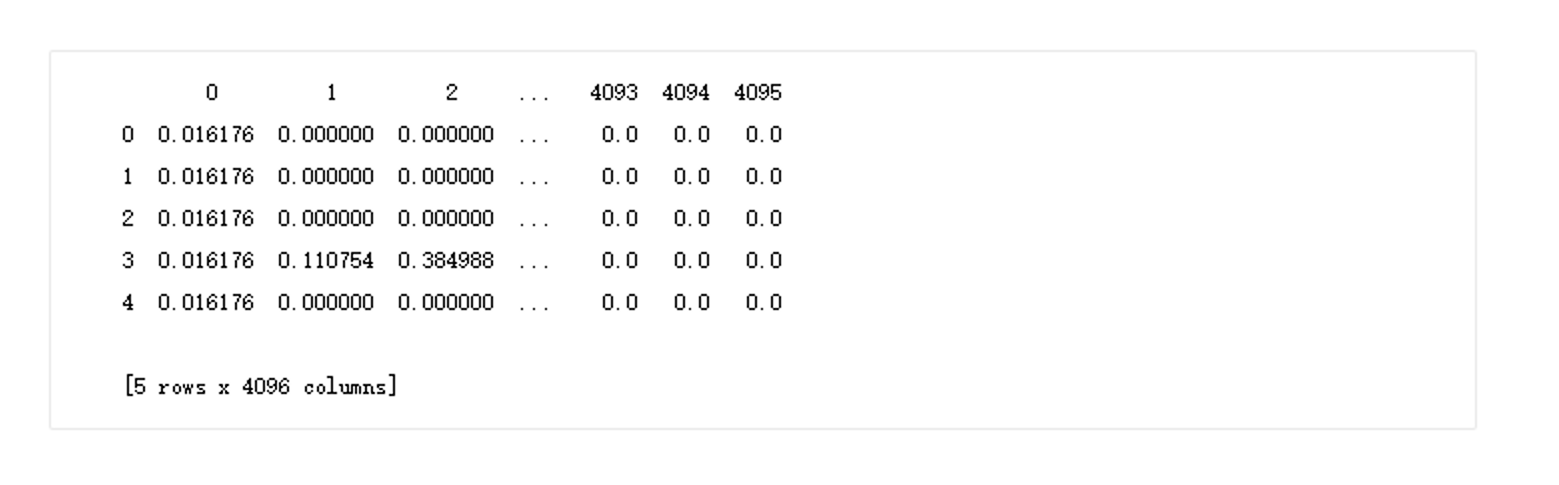
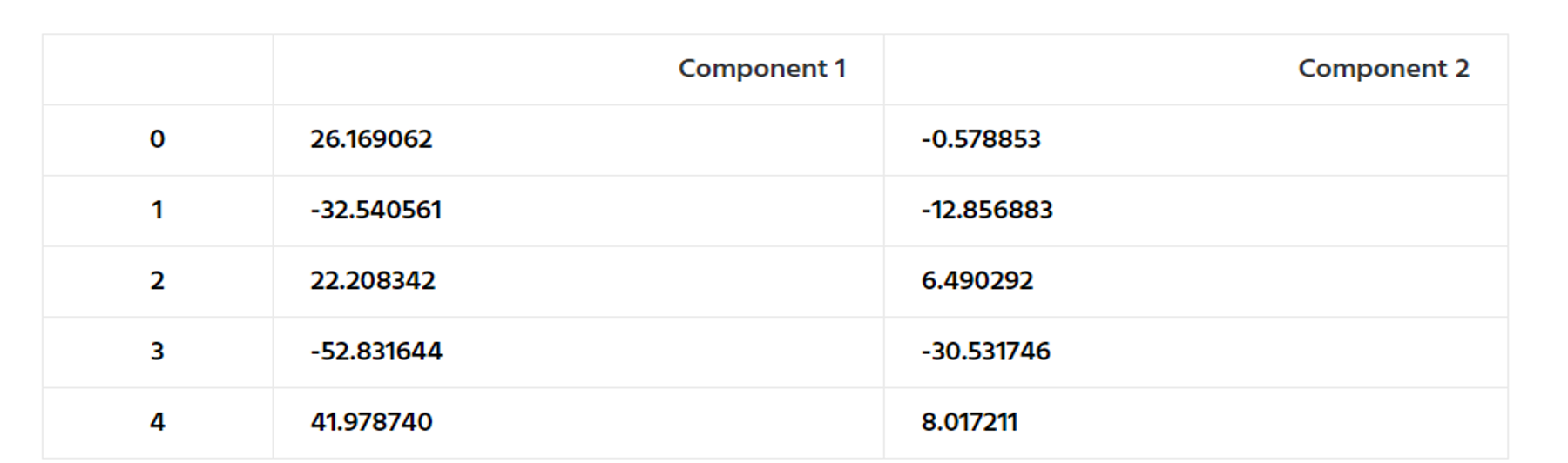
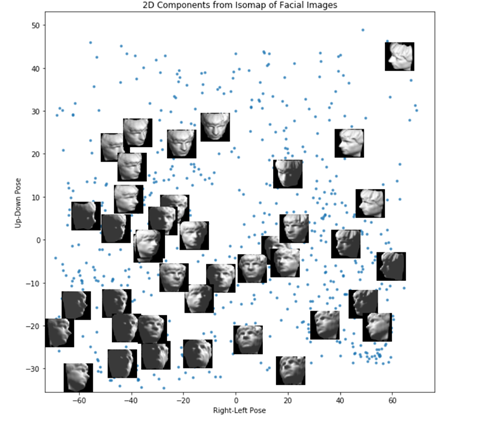
参考资料

https://benalexkeen.com/isomap-for-dimensionality-reduction-in-python/

 

https://towardsdatascience.com/decomposing-non-linearity-with-isomap-32cf1e95a483

 

https://scikit-learn.org/stable/auto_examples/manifold/plot_lle_digits.html#sphx-glr-auto-examples-manifold-plot-lle-digits-py

 

http://benalexkeen.com/implementing-djikstras-shortest-path-algorithm-with-python/

标签：映射,距离,测地线,降维,算法,欧式,数据,度量
来源： https://www.cnblogs.com/LuckCoder/p/14257343.html