题解 P5566 【[SDOI2008]红黑树】

最近在刷平衡树，看到标题就进来了，没想到是个dp？？？看了看，发现可以贪心，于是就有了这篇题解。

分析：

因为红黑树本身的性质，所以我们可以通过画图来枚举所有情况：

---

先把每一个节点看成黑色的，通过红黑树性质来把一些结点变成红色的。

• \(case1:\)

如图：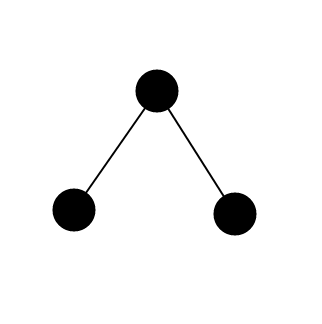

最亏的一种情况，两个黑色节点没变出来一个红色节点。

• \(case2:\)

如图：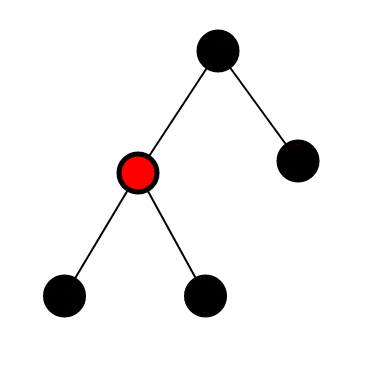

三个黑色节点变成一个红色节点，有点浪费。

• \(case3:\)

如图：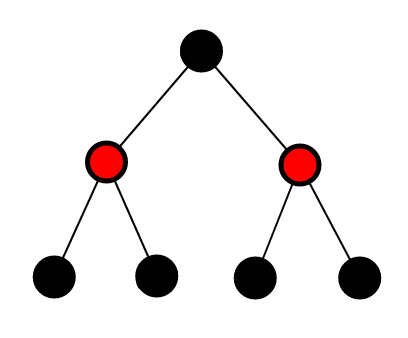

此时四个黑色节点变成两个红色节点，黑色节点的利用率最大。

---

所以，贪心就很明确了。

\(\text{code:}\)

#include "cstdio"
int n, ans, k;
int main()
{
	scanf("%d", &n);
	k = n + 1;
	while (k > 1)
	{
		ans += k & 1;
		k >>= 1;
	}
	printf("%d\n", ans);
	k = n + 1;
	ans = 0;
	while (k > 1)
	{
		if (k == 2)
			ans++, k--;
		else if ((k & 3) == 1)
			ans += ((k >> 2) << 1) - 1, k >>= 2, k++;
		else if ((k & 3) == 2)
			ans += ((k >> 2) << 1), k >>= 2, k++;
		else if ((k & 3) == 3)
			ans += ((k >> 2) << 1) + 1, k >>= 2, k++;
		else
			ans += (k >> 1), k >>= 2;
	}
	printf("%d", ans);
	return 0;
}

---

关于DP

自己想了一种方法，不过好像有亿点点慢。

以最小值为例：

用 \(R_{(i,j)}\) 表示 \(i\) 个结点，黑高度为 \(j\) 的红根树中红色结点最小值；

\(B_{(i,j)}\) 表示 \(i\) 个结点，黑高度为 \(j\) 的黑根树中红色结点最小值。

\(\therefore R_{(i,j)}=\min\left({R_{(i,j)},B_{(k,j-1)}+B_{(i-k-1,j-1)}+1}\right)\quad(i\leq k\leq i-2)\)；

\(\therefore B_{(i,j)}=\min\left({B_{(k,j-1)},B_{(i-k-1,j-1)},R_{(k,j)}+R_{(i-k-1,j)},R_{(k,j)}+B_{(i-k-1,j-1)}}\right)\quad(i\leq k\leq i-2)\)；

---

代码就不放了，贪心它不香吗？

标签：结点,P5566,++,题解,else,leq,ans,SDOI2008,节点
来源： https://www.cnblogs.com/nakiri-ayame-suki/p/14044111.html