长春
作者:互联网
B-Fraction
tag:签到题
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+100;
ll a[maxn],b[maxn];
int main()
{
int T;scanf("%d",&T);int t=0;
while(T--)
{
int n;scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
for(int i=1;i<=n;i++)scanf("%lld",&b[i]);
ll p=b[n],q=a[n],temp,temq;
for(int i=n-1;i>=1;i--)
{
temp=b[i]*q,temq=a[i]*q+p;
swap(p,temp),swap(temq,q);
}
ll g=__gcd(p,q);
printf("Case #%d: %lld %lld\n",++t,p/g,q/g);
}
}
G-Instability
题意:给定一张无向图n<51,问其中包含qaq[三个点两两不相连或者三个点两两相连]的集合数
注意点:1.敲一个组合数表不然可能会tle
题解:算是结论题Ramsey定理。
结论:六个点及以上的集合必然包含qaq;
证明:连边为红,不连边为蓝
由鸽巢定理得,\(\forall a\in s, 与它相连的5条边至少有三条同色,假设为红。这三条边都蓝色,就构成蓝色三角形,存在红色,就有红色三角形\)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define debug(x) cout<<#x<<':'<<x<<endl;
const int mod=1e9+7;
int d[100][100],c[100][100];
bool check(int i ,int j,int k){return d[i][j]==d[j][k]&&d[j][k]==d[k][i];}
int main()
{
ll T,n,m,u,v;
scanf("%lld",&T);int t=0;
for(int i=0;i<51;i++)//组合数
c[i][0]=c[i][i]=1;
for(int i=2;i<51;i++) {
for (int j = 1; j < i; j++)
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
}
while(T--)
{
scanf("%lld%lld",&n,&m);
memset(d,0,sizeof(d));
ll ans=0;
while(m--)
{
scanf("%lld%lld",&u,&v);d[u][v]=d[v][u]=1;
}
if(n>=6)
for(int w=6;w<=n;w++)
ans=(ans+c[n][w])%mod;
if(n>=5)
{
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
for(int k=j+1;k<=n;k++)
for(int q=k+1;q<=n;q++)
for(int p=q+1;p<=n;p++)
if(check(i,j,k)||check(i,j,q)||check(i,k,q)||check(j,k,q)||check(i,j,p)||check(i,k,p)||check(i,q,p)||check(j,k,p)||check(j,q,p)||check(k,p,q)) ans++;
}
ans%=mod;
if(n>=4)
{
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
for(int k=j+1;k<=n;k++)
for(int q=k+1;q<=n;q++)
if(check(i,j,k)||check(i,j,q)||check(i,k,q)||check(j,k,q)) ans++;
}
ans%=mod;
if(n>=3)
{
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
for(int k=j+1;k<=n;k++)
if(check(i,j,k)) ans++;
}
printf("Case #%d: %lld\n",++t,ans%mod);
}
}
K- Binary Indexed Tree
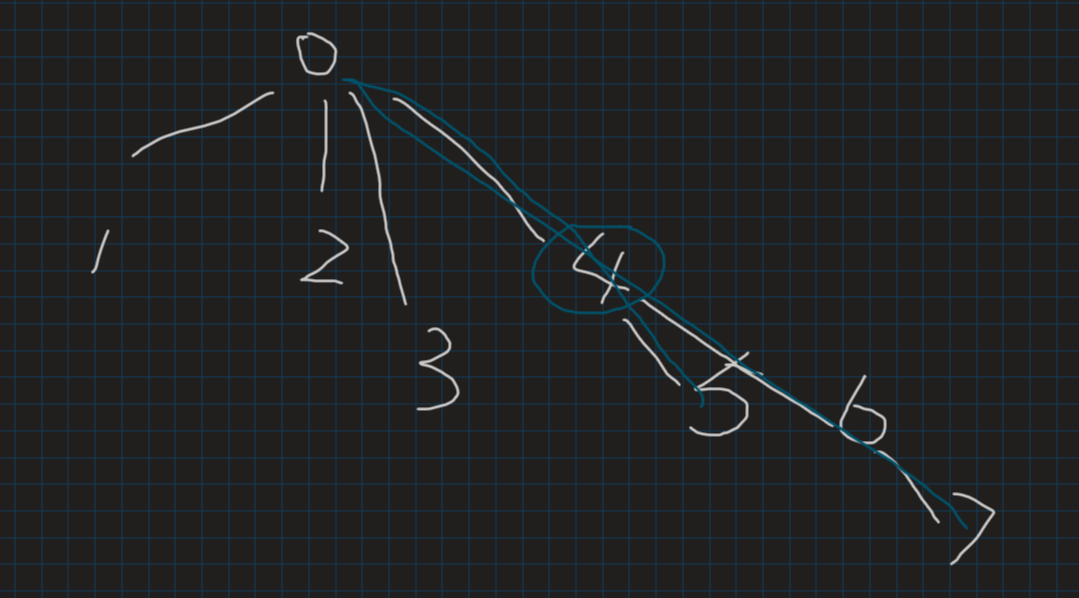
题意:求:\(ans=\sum_{i=0}^{n}g(i)+\sum_{i=0}^n\sum_{j=0}^nlcp(g(i,j))\),g(i)表示i转二进制后1的数量。
如图,连线表示相差一个lowbit,在进行一次操作的时候,0-4这段被抵消了,于是可以转换题意如上
题解:对于每一位i(i从1开始),pow2[i]一组,组数记为tuan,除组数以外的1的数量记为san
以第三位为例,可以分成tuan=1,san=0;第四位tuan=0,san=1;
为了把0算作一个数,所以n++,n表示从0开始的数字的数量
tuan=n/pow2[i],san=(n%pow2[i]/pow2[i-1])*(n%pow2[i-1])
遍历每一位的时候,
ansleft+=n·(tuan·pow2[i-1]+san)//把该位是1的个数加上
ansright+=tuan·pow2[i-1]·pow2[i-1]+san·san//因为对于每一组它们的lcp都包括该位
pow2[i]: 32 16 8 4 2 1
num=0 0 0 0 0 0 0
num=1 0 0 0 0 0 1
num=2 0 0 0 0 1 0
num=3 0 0 0 0 1 1
num=4 0 0 0 1 0 0
num=5 0 0 0 1 0 1
num=6 0 0 0 1 1 0
num=7 0 0 0 1 1 1
num=8 0 0 1 0 0 0
注意点:我都怀疑这题是在考大数,几乎每一个数都要加%mod,我写了一遍python[python不给交,以及注意python:mod=int(1e9+7),要转int]确认思路没问题了才继续改c++
python:
pow2=[1,]
t=1;
mod=int(1e9+7)
for i in range(1,64):
t*=2
pow2.append(int(t))
T=int (input())
for t in range(1,T+1):
n=int (input())
ansleft=int(0)
ansright=int(0)
n+=1
for i in range(63,0,-1):
san=int(((n%pow2[i])//pow2[i-1])*(n%pow2[i-1]))
tuan=int(n//pow2[i])
ansright+=int(tuan*pow2[i-1]*pow2[i-1]+san*san)
ansleft+=int(n*(tuan*pow2[i-1]+san))
print("Case #",end="")
print(t,end="")
print(": ",end="")
print(int((ansleft%mod+mod-ansright%mod)%mod))
c++
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
#define debug(x) cout<<#x<<':'<<x<<endl;
const int mod=1e9+7;
ull pow2[65];
ull mul(ull a,ull b){a%=mod,b%=mod;return a*b%mod;}
int main()
{
pow2[0]=1;
for(int i=1;i<64;i++)pow2[i]=pow2[i-1]*2;
int T,t=0;scanf("%d",&T);
while(T--)
{
ull n;scanf("%llu",&n);n++;//n为算上零后的个数,
ull ansleft=0,ansright=0;
for(int i=63;i>=1;i--)
{
ull san=mul((n%pow2[i])/pow2[i-1],n%pow2[i-1]);
ull tuan=(n/pow2[i])%mod;
ansright=(ansright+mul(tuan,mul(pow2[i-1],pow2[i-1]))+mul(san,san))%mod;
// ansright=((ansright+(((tuan*(pow2[i-1]%mod))%mod)*(pow2[i-1]%mod))%mod+(san*san)%mod)%mod)%mod;
ansleft=(ansleft+mul(n,mul(tuan,pow2[i-1])+san))%mod;
//ansleft=(ansleft+(n%mod)*(tuan*pow2[i-1]%mod+san))%mod;
}
printf("Case #%d: %lld\n",++t,(ansleft+mod-ansright)%mod);
}
}
标签:tuan,san,pow2,int,num,长春,mod 来源: https://www.cnblogs.com/zx0710/p/13965776.html