2020年HZNU天梯训练赛 Round 3

时间：2020.7.17 22 180

完成情况：

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
√	√	√	√	√	√	√	√	√	√				√

√ 当场做出来 ※做了一半来 ✘补题补出来

7-1 到底有多二 (15分)

一个整数“犯二的程度”定义为该数字中包含2的个数与其位数的比值。如果这个数是负数，则程度增加0.5倍；如果还是个偶数，则再增加1倍。例如数字-13142223336是个11位数，其中有3个2，并且是负数，也是偶数，则它的犯二程度计算为：3/11×1.5×2×100%，约为81.82%。本题就请你计算一个给定整数到底有多二。

输入格式：

输入第一行给出一个不超过50位的整数N。

输出格式：

在一行中输出N犯二的程度，保留小数点后两位。

输入样例：

-13142223336

输出样例：

81.82%

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
typedef long long LL;

int main()
{
	char s[55];
	int cnt=0,num=0,begin=0;
	cin>>s;
	double p=1;
	if(s[0]=='-'){p*=1.5;begin=1;}
	if((s[strlen(s)-1]-'0')%2==0)p*=2;
	
	for(int i=begin;i<strlen(s);i++)
	{
		if((s[i]-'0')%10==2)cnt++;
		num++;
	}
	//cout<<cnt<<"***"<<num<<endl;
	double ans=(double)cnt/(double)num*p*100;
	printf("%.2lf%%",ans);
    return 0;
}

7-2 大笨钟 (10分)

微博上有个自称“大笨钟V”的家伙，每天敲钟催促码农们爱惜身体早点睡觉。不过由于笨钟自己作息也不是很规律，所以敲钟并不定时。一般敲钟的点数是根据敲钟时间而定的，如果正好在某个整点敲，那么“当”数就等于那个整点数；如果过了整点，就敲下一个整点数。另外，虽然一天有24小时，钟却是只在后半天敲1~12下。例如在23:00敲钟，就是“当当当当当当当当当当当”，而到了23:01就会是“当当当当当当当当当当当当”。在午夜00:00到中午12:00期间（端点时间包括在内），笨钟是不敲的。

下面就请你写个程序，根据当前时间替大笨钟敲钟。

输入格式：

输入第一行按照hh:mm的格式给出当前时间。其中hh是小时，在00到23之间；mm是分钟，在00到59之间。

输出格式：

根据当前时间替大笨钟敲钟，即在一行中输出相应数量个Dang。如果不是敲钟期，则输出：

Only hh:mm.  Too early to Dang.

其中hh:mm是输入的时间。

输入样例1：

19:05

输出样例1：

DangDangDangDangDangDangDangDang

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
int main()
{
    int a,b;
    scanf("%d:%d",&a,&b);
    if(a<12||(a==12&&b==00))
	{
        if(a<10&&b>10)printf("Only 0%d:%d.  Too early to Dang.\n",a,b);
        if(a<10&&b<10)printf("Only 0%d:0%d.  Too early to Dang.\n",a,b);
        if(a>10&&b<10)printf("Only %d:0%d.  Too early to Dang.\n",a,b);
    	if(a>10&&b>10)printf("Only %d:%d.  Too early to Dang.\n",a,b);
    }
    else
    {
        int x;
        if(b==00) {for(int i=0;i<a-12;i++)cout<<"Dang";}
        else {for(int i=0;i<a-11;i++)cout<<"Dang";}
    }
    return 0;
}

7-3 谁先倒 (15分)

划拳是古老中国酒文化的一个有趣的组成部分。酒桌上两人划拳的方法为：每人口中喊出一个数字，同时用手比划出一个数字。如果谁比划出的数字正好等于两人喊出的数字之和，谁就输了，输家罚一杯酒。两人同赢或两人同输则继续下一轮，直到唯一的赢家出现。

下面给出甲、乙两人的酒量（最多能喝多少杯不倒）和划拳记录，请你判断两个人谁先倒。

输入格式：

输入第一行先后给出甲、乙两人的酒量（不超过100的非负整数），以空格分隔。下一行给出一个正整数N（≤100），随后N行，每行给出一轮划拳的记录，格式为：

甲喊 甲划 乙喊 乙划

其中喊是喊出的数字，划是划出的数字，均为不超过100的正整数（两只手一起划）。

输出格式：

在第一行中输出先倒下的那个人：A代表甲，B代表乙。第二行中输出没倒的那个人喝了多少杯。题目保证有一个人倒下。注意程序处理到有人倒下就终止，后面的数据不必处理。

输入样例：

1 1
6
8 10 9 12
5 10 5 10
3 8 5 12
12 18 1 13
4 16 12 15
15 1 1 16

输出样例：

A
1

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
typedef long long LL;

int main()
{
	int a,b,n,x,y,z,w,aa,bb;
	cin>>a>>b>>n;
	aa=a;bb=b;
	while(n--)
	{
		cin>>x>>y>>z>>w;
		if(x+z==y&&x+z!=w)a--;
		if(x+z==w&&x+z!=y)b--;
		if(a==-1){cout<<"A"<<endl<<bb-b;break;}
		if(b==-1){cout<<"B"<<endl<<aa-a;break;}
	}

    return 0;
}

7-4 帅到没朋友 (20分)

当芸芸众生忙着在朋友圈中发照片的时候，总有一些人因为太帅而没有朋友。本题就要求你找出那些帅到没有朋友的人。

输入格式：

输入第一行给出一个正整数N（≤100），是已知朋友圈的个数；随后N行，每行首先给出一个正整数K（≤1000），为朋友圈中的人数，然后列出一个朋友圈内的所有人——为方便起见，每人对应一个ID号，为5位数字（从00000到99999），ID间以空格分隔；之后给出一个正整数M（≤10000），为待查询的人数；随后一行中列出M个待查询的ID，以空格分隔。

注意：没有朋友的人可以是根本没安装“朋友圈”，也可以是只有自己一个人在朋友圈的人。虽然有个别自恋狂会自己把自己反复加进朋友圈，但题目保证所有K超过1的朋友圈里都至少有2个不同的人。

输出格式：

按输入的顺序输出那些帅到没朋友的人。ID间用1个空格分隔，行的首尾不得有多余空格。如果没有人太帅，则输出No one is handsome。

注意：同一个人可以被查询多次，但只输出一次。

输入样例1：

3
3 11111 22222 55555
2 33333 44444
4 55555 66666 99999 77777
8
55555 44444 10000 88888 22222 11111 23333 88888

输出样例1：

10000 88888 23333

输入样例2：

3
3 11111 22222 55555
2 33333 44444
4 55555 66666 99999 77777
4
55555 44444 22222 11111

输出样例2：

No one is handsome

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
typedef long long LL;
int a[100000]={0};    

int main()
{
  	int n,k,x,m,sum=0;
    cin>>n;   
    for(int i=1;i<=n;i++)    
    {    
        cin>>k;    
        for(int j=1;j<=k;j++)    
        {    
            cin>>x;    
            if(k!=1) a[x]+=k-1;   
        }    
    }    
    cin>>m ;  
    for(int i=1;i<=m;i++)    
    {    
        cin>>x;     
        if(a[x]==0)    
        {    
            if(sum!=0) cout<<" ";    
            printf("%05d",x);    
            a[x]=-1; 
            sum++;    
        }    
    }     
    if(sum==0)  cout<<"No one is handsome" <<endl;    
    return 0;
}

7-5 重要的话说三遍 (5分)

这道超级简单的题目没有任何输入。

你只需要把这句很重要的话 —— “I'm gonna WIN!”——连续输出三遍就可以了。

注意每遍占一行，除了每行的回车不能有任何多余字符。

I'm gonna WIN!
I'm gonna WIN!
I'm gonna WIN!

7-6 奇偶分家 (10分)

给定N个正整数，请统计奇数和偶数各有多少个？

输入格式：

输入第一行给出一个正整N（≤1000）；第2行给出N个非负整数，以空格分隔。

输出格式：

在一行中先后输出奇数的个数、偶数的个数。中间以1个空格分隔。

输入样例：

9
88 74 101 26 15 0 34 22 77

输出样例：

3 6

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
typedef long long LL;

int main()
{
	int n,x,o=0,j=0;
	cin>>n;
	while(n--)
	{	
		cin>>x;
		if(x%2==0)	o++;
		else	j++;
		
	} 
   	cout<<j<<" "<<o;
    return 0;
}

7-7 输出GPLT (20分)

给定一个长度不超过10000的、仅由英文字母构成的字符串。请将字符重新调整顺序，按GPLTGPLT....这样的顺序输出，并忽略其它字符。当然，四种字符（不区分大小写）的个数不一定是一样多的，若某种字符已经输出完，则余下的字符仍按GPLT的顺序打印，直到所有字符都被输出。

输入格式：

输入在一行中给出一个长度不超过10000的、仅由英文字母构成的非空字符串。

输出格式：

在一行中按题目要求输出排序后的字符串。题目保证输出非空。

输入样例：

pcTclnGloRgLrtLhgljkLhGFauPewSKgt

输出样例：

GPLTGPLTGLTGLGLL

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
typedef long long LL;

int main()
{
	string s;
    cin>>s;
    int g=0,p=0,l=0,t=0;
    for(int i=0;i<s.size();i++)
    {
        if(s[i]=='G'||s[i]=='g')g++;
    	if(s[i]=='P'||s[i]=='p')p++;
    	if(s[i]=='L'||s[i]=='l')l++;
        if(s[i]=='T'||s[i]=='t')t++;
    }
    while(g||p||l||t)
    {
        if(g){cout<<"G";g--;}
        if(p){cout<<"P";p--;}
        if(l){cout<<"L";l--;}
        if(t){cout<<"T";t--;}
    }
    return 0;
}

7-8 后天 (5分)

如果今天是星期三，后天就是星期五；如果今天是星期六，后天就是星期一。我们用数字1到7对应星期一到星期日。给定某一天，请你输出那天的“后天”是星期几。

输入格式：

输入第一行给出一个正整数D（1 ≤ D ≤ 7），代表星期里的某一天。

输出格式：

在一行中输出D天的后天是星期几。

输入样例：

3

输出样例：

5

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
typedef long long LL;

int main()
{
	int d;
	cin>>d;
	if(d+2>7)
		cout<<d+2-7;
	else cout<<d+2;
    return 0;
}

7-9 抢红包 (25分)

没有人没抢过红包吧…… 这里给出N个人之间互相发红包、抢红包的记录，请你统计一下他们抢红包的收获。

输入格式：

输入第一行给出一个正整数N（≤104），即参与发红包和抢红包的总人数，则这些人从1到N编号。随后N行，第i行给出编号为i的人发红包的记录，格式如下：

K**N1P1⋯NKP**K

其中K（0≤K≤20）是发出去的红包个数，N**i是抢到红包的人的编号，P**i（>0）是其抢到的红包金额（以分为单位）。注意：对于同一个人发出的红包，每人最多只能抢1次，不能重复抢。

输出格式：

按照收入金额从高到低的递减顺序输出每个人的编号和收入金额（以元为单位，输出小数点后2位）。每个人的信息占一行，两数字间有1个空格。如果收入金额有并列，则按抢到红包的个数递减输出；如果还有并列，则按个人编号递增输出。

输入样例：

10
3 2 22 10 58 8 125
5 1 345 3 211 5 233 7 13 8 101
1 7 8800
2 1 1000 2 1000
2 4 250 10 320
6 5 11 9 22 8 33 7 44 10 55 4 2
1 3 8800
2 1 23 2 123
1 8 250
4 2 121 4 516 7 112 9 10

输出样例：

1 11.63
2 3.63
8 3.63
3 2.11
7 1.69
6 -1.67
9 -2.18
10 -3.26
5 -3.26
4 -12.32

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
typedef long long LL;
//int p[10005]={0};    
struct node
{
	int id,num, v;
}p[10000];
bool cmp(struct node a,struct node b)
{
	if(a.v!=b.v)			return a.v>b.v;
	else if(a.num!=b.num)	return a.num>b.num;	
	else if(a.id!=b.id)		return a.id<b.id;	
}
int main()
{
  	int n,k,x,y,sum=0;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		sum=0;
		p[i].id=i;
		cin>>k;
		for(int j=1;j<=k;j++)
		{
			cin>>x>>y;
			p[x].v+=y;
			p[x].num++; 
			sum=sum+y;
		}
		p[i].v-=sum;
	} 

	sort(p+1,p+n+1,cmp);
	for(int i=1;i<=n;i++)	printf("%d %.2lf\n",p[i].id,(double)p[i].v/100);
	return 0;

}

7-10 排座位 (25分)

布置宴席最微妙的事情，就是给前来参宴的各位宾客安排座位。无论如何，总不能把两个死对头排到同一张宴会桌旁！这个艰巨任务现在就交给你，对任何一对客人，请编写程序告诉主人他们是否能被安排同席。

输入格式：

输入第一行给出3个正整数：N（≤100），即前来参宴的宾客总人数，则这些人从1到N编号；M为已知两两宾客之间的关系数；K为查询的条数。随后M行，每行给出一对宾客之间的关系，格式为：宾客1 宾客2 关系，其中关系为1表示是朋友，-1表示是死对头。注意两个人不可能既是朋友又是敌人。最后K行，每行给出一对需要查询的宾客编号。

这里假设朋友的朋友也是朋友。但敌人的敌人并不一定就是朋友，朋友的敌人也不一定是敌人。只有单纯直接的敌对关系才是绝对不能同席的。

输出格式：

对每个查询输出一行结果：如果两位宾客之间是朋友，且没有敌对关系，则输出No problem；如果他们之间并不是朋友，但也不敌对，则输出OK；如果他们之间有敌对，然而也有共同的朋友，则输出OK but...；如果他们之间只有敌对关系，则输出No way。

输入样例：

7 8 4
5 6 1
2 7 -1
1 3 1
3 4 1
6 7 -1
1 2 1
1 4 1
2 3 -1
3 4
5 7
2 3
7 2

输出样例：

No problem
OK
OK but...
No way

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
typedef long long LL;
//int p[10005]={0};  
int a[101][101],b[101];  
/*//并查集板子 
int find(int x)
{
   //while(x!=pre[x])  //如果该结点的父结点不是它自身
　　　　//x=pre[x];  //那么就继续找它的父结点的父结点
　 return x==pre[x]?x:find(pre[x]);
}
//查找函数：用于查找结点的父结点。
void Union(int x,int y)
{
　　int fx=find(x);  //找到x的根结点
　　int fy=find(y);  //找到y的根结点
　　if(fx!=fy)  //如果x和y的根结点不相同（x和y不属于同一个联通分支）
　　　　pre[fx]=fy; //就把x的根结点的父结点改为y的根结点
}//合并函数 
*/
int find(int x)
{
    return b[x]==x?x:b[x]=find(b[x]);
}
int main()
{
    int n,m,k,x,y,z,p,q;
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)b[i]=i;
    for(int i=0;i<m;i++)
    {
        cin>>x>>y>>z;
        if(z==-1) a[x][y]=a[y][x]=1;
        else 
		{
            int x1=find(x);//查找 
            int y1=find(y);
            if(x1!=y1) b[x1]=y1;//合并
        }
    }
    for(int i=0;i<k;i++)
    {
        cin>>p>>q;
        int p1=find(p);
        int q1=find(q);
        if(q1==p1&&!a[p][q]) printf("No problem\n");
        else if(q1==p1&&a[p][q]) printf("OK but...\n");
        else if(q1!=p1&&!a[p][q]) printf("OK\n");
        else if(q1!=p1&&a[p][q]) printf("No way\n");
    }
    return 0;
}

7-11 玩转二叉树 (25分)

给定一棵二叉树的中序遍历和前序遍历，请你先将树做个镜面反转，再输出反转后的层序遍历的序列。所谓镜面反转，是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。

输入格式：

输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。

输出格式：

在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
1 2 3 4 5 6 7
4 1 3 2 6 5 7

输出样例：

4 6 1 7 5 3 2

7-12 关于堆的判断 (25分)

将一系列给定数字顺序插入一个初始为空的小顶堆H[]。随后判断一系列相关命题是否为真。命题分下列几种：

• x is the root：x是根结点；
• x and y are siblings：x和y是兄弟结点；
• x is the parent of y：x是y的父结点；
• x is a child of y：x是y的一个子结点。

输入格式：

每组测试第1行包含2个正整数N（≤ 1000）和M（≤ 20），分别是插入元素的个数、以及需要判断的命题数。下一行给出区间[−10000,10000]内的N个要被插入一个初始为空的小顶堆的整数。之后M行，每行给出一个命题。题目保证命题中的结点键值都是存在的。

输出格式：

对输入的每个命题，如果其为真，则在一行中输出T，否则输出F。

输入样例：

5 4
46 23 26 24 10
24 is the root
26 and 23 are siblings
46 is the parent of 23
23 is a child of 10

输出样例：

F
T
F
T

7-13 天梯地图 (30分)

本题要求你实现一个天梯赛专属在线地图，队员输入自己学校所在地和赛场地点后，该地图应该推荐两条路线：一条是最快到达路线；一条是最短距离的路线。题目保证对任意的查询请求，地图上都至少存在一条可达路线。

输入格式：

输入在第一行给出两个正整数N（2 ≤ N ≤ 500）和M，分别为地图中所有标记地点的个数和连接地点的道路条数。随后M行，每行按如下格式给出一条道路的信息：

V1 V2 one-way length time

其中V1和V2是道路的两个端点的编号（从0到N-1）；如果该道路是从V1到V2的单行线，则one-way为1，否则为0；length是道路的长度；time是通过该路所需要的时间。最后给出一对起点和终点的编号。

输出格式：

首先按下列格式输出最快到达的时间T和用节点编号表示的路线：

Time = T: 起点 => 节点1 => ... => 终点

然后在下一行按下列格式输出最短距离D和用节点编号表示的路线：

Distance = D: 起点 => 节点1 => ... => 终点

如果最快到达路线不唯一，则输出几条最快路线中最短的那条，题目保证这条路线是唯一的。而如果最短距离的路线不唯一，则输出途径节点数最少的那条，题目保证这条路线是唯一的。

如果这两条路线是完全一样的，则按下列格式输出：

Time = T; Distance = D: 起点 => 节点1 => ... => 终点

输入样例1：

10 15
0 1 0 1 1
8 0 0 1 1
4 8 1 1 1
5 4 0 2 3
5 9 1 1 4
0 6 0 1 1
7 3 1 1 2
8 3 1 1 2
2 5 0 2 2
2 1 1 1 1
1 5 0 1 3
1 4 0 1 1
9 7 1 1 3
3 1 0 2 5
6 3 1 2 1
5 3

输出样例1：

Time = 6: 5 => 4 => 8 => 3
Distance = 3: 5 => 1 => 3

输入样例2：

7 9
0 4 1 1 1
1 6 1 3 1
2 6 1 1 1
2 5 1 2 2
3 0 0 1 1
3 1 1 3 1
3 2 1 2 1
4 5 0 2 2
6 5 1 2 1
3 5

输出样例2：

Time = 3; Distance = 4: 3 => 2 => 5

7-14 喊山 (30分)

喊山，是人双手围在嘴边成喇叭状，对着远方高山发出“喂—喂喂—喂喂喂……”的呼唤。呼唤声通过空气的传递，回荡于深谷之间，传送到人们耳中，发出约定俗成的“讯号”，达到声讯传递交流的目的。原来它是彝族先民用来求援呼救的“讯号”，慢慢地人们在生活实践中发现了它的实用价值，便把它作为一种交流工具世代传袭使用。（图文摘自：http://news.xrxxw.com/newsshow-8018.html）

一个山头呼喊的声音可以被临近的山头同时听到。题目假设每个山头最多有两个能听到它的临近山头。给定任意一个发出原始信号的山头，本题请你找出这个信号最远能传达到的地方。

输入格式：

输入第一行给出3个正整数n、m和k，其中n（≤10000）是总的山头数（于是假设每个山头从1到n编号）。接下来的m行，每行给出2个不超过n的正整数，数字间用空格分开，分别代表可以听到彼此的两个山头的编号。这里保证每一对山头只被输入一次，不会有重复的关系输入。最后一行给出k（≤10）个不超过n的正整数，数字间用空格分开，代表需要查询的山头的编号。

输出格式：

依次对于输入中的每个被查询的山头，在一行中输出其发出的呼喊能够连锁传达到的最远的那个山头。注意：被输出的首先必须是被查询的个山头能连锁传到的。若这样的山头不只一个，则输出编号最小的那个。若此山头的呼喊无法传到任何其他山头，则输出0。

输入样例：

7 5 4
1 2
2 3
3 1
4 5
5 6
1 4 5 7

输出样例：

2
6
4
0

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
struct node{
    int x,num;
}s,s2;
vector<int> v[10005];
int vis[10005],maxx,ans;
void BFS(int t)
{
    memset(vis,0,sizeof(vis));
    queue<node> q;
    s.x=t,s.num=1;
    q.push(s);
    maxx=-1;vis[t]=1;ans=t;
    while(!q.empty())
    {
        node s1=q.front();q.pop();
        if(s1.num>maxx) maxx=s1.num,ans=s1.x;
        else if(s1.num==maxx) ans=min(s1.x,ans);
        for(int i=0;i<v[s1.x].size();i++)
        {
            if(!vis[v[s1.x][i]])
            {
                s2.x=v[s1.x][i],s2.num=s1.num+1;
                q.push(s2);
                vis[s2.x]=1;
            }
        }
    }
}
int main()
{
    int n,m,k,a,b,t;
    cin>>n>>m>>k;
    for(int i=0;i<m;i++)
    {
        cin>>a>>b; 
        v[a].push_back(b);
        v[b].push_back(a);
    }
    for(int i=0;i<k;i++)
    {
        cin>>t;
        BFS(t);
        if(ans==t)cout<<"0"<<endl;
        else cout<<ans<<endl;       
	}
	return 0;
}

7-15 长城 (30分)

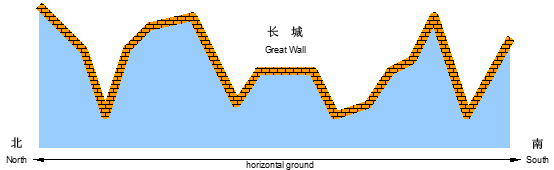
正如我们所知，中国古代长城的建造是为了抵御外敌入侵。在长城上，建造了许多烽火台。每个烽火台都监视着一个特定的地区范围。一旦某个地区有外敌入侵，值守在对应烽火台上的士兵就会将敌情通报给周围的烽火台，并迅速接力地传递到总部。

现在如图1所示，若水平为南北方向、垂直为海拔高度方向，假设长城就是依次相联的一系列线段，而且在此范围内的任一垂直线与这些线段有且仅有唯一的交点。

图 1

进一步地，假设烽火台只能建造在线段的端点处。我们认为烽火台本身是没有高度的，每个烽火台只负责向北方（图1中向左）瞭望，而且一旦有外敌入侵，只要敌人与烽火台之间未被山体遮挡，哨兵就会立即察觉。当然，按照这一军规，对于南侧的敌情各烽火台并不负责任。一旦哨兵发现敌情，他就会立即以狼烟或烽火的形式，向其南方的烽火台传递警报，直到位于最南侧的总部。

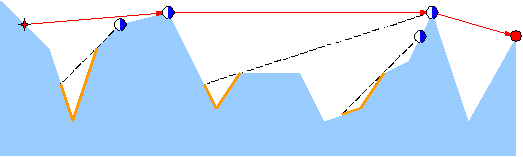
以图2中的长城为例，负责守卫的四个烽火台用蓝白圆点示意，最南侧的总部用红色圆点示意。如果红色星形标示的地方出现敌情，将被哨兵们发现并沿红色折线将警报传递到总部。当然，就这个例子而言只需两个烽火台的协作，但其他位置的敌情可能需要更多。

然而反过来，即便这里的4个烽火台全部参与，依然有不能覆盖的（黄色）区域。

图 2

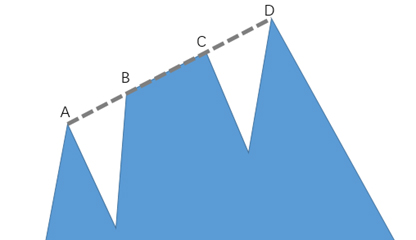
另外，为避免歧义，我们在这里约定，与某个烽火台的视线刚好相切的区域都认为可以被该烽火台所监视。以图3中的长城为例，若A、B、C、D点均共线，且在D点设置一处烽火台，则A、B、C以及线段BC上的任何一点都在该烽火台的监视范围之内。

图 3

好了，倘若你是秦始皇的太尉，为不致出现更多孟姜女式的悲剧，如何在保证长城安全的前提下，使消耗的民力（建造的烽火台）最少呢？

输入格式：

输入在第一行给出一个正整数N（3 ≤ N ≤105），即刻画长城边缘的折线顶点（含起点和终点）数。随后N行，每行给出一个顶点的x和y坐标，其间以空格分隔。注意顶点从南到北依次给出，第一个顶点为总部所在位置。坐标为区间[−109,109)内的整数，且没有重合点。

输出格式：

在一行中输出所需建造烽火台（不含总部）的最少数目。

输入样例：

10
67 32
48 -49
32 53
22 -44
19 22
11 40
10 -65
-1 -23
-3 31
-7 59

输出样例：

2

标签：输出,10,int,HZNU,样例,2020,格式,训练赛,输入
来源： https://www.cnblogs.com/zjy0217/p/13353858.html