P1231 教辅的组成 【网络流】【最大流】
作者:互联网
题目背景
滚粗了的HansBug在收拾旧语文书,然而他发现了什么奇妙的东西。
题目描述
蒟蒻HansBug在一本语文书里面发现了一本答案,然而他却明明记得这书应该还包含一份练习题。然而出现在他眼前的书多得数不胜数,其中有书,有答案,有练习册。已知一个完整的书册均应该包含且仅包含一本书、一本练习册和一份答案,然而现在全都乱做了一团。许多书上面的字迹都已经模糊了,然而HansBug还是可以大致判断这是一本书还是练习册或答案,并且能够大致知道一本书和答案以及一本书和练习册的对应关系(即仅仅知道某书和某答案、某书和某练习册有可能相对应,除此以外的均不可能对应)。既然如此,HansBug想知道在这样的情况下,最多可能同时组合成多少个完整的书册。
输入格式
第一行包含三个正整数N1、N2、N3,分别表示书的个数、练习册的个数和答案的个数。
第二行包含一个正整数M1,表示书和练习册可能的对应关系个数。
接下来M1行每行包含两个正整数x、y,表示第x本书和第y本练习册可能对应。(1<=x<=N1,1<=y<=N2)
第M1+3行包含一个正整数M2,表述书和答案可能的对应关系个数。
接下来M2行每行包含两个正整数x、y,表示第x本书和第y本答案可能对应。(1<=x<=N1,1<=y<=N3)
输出格式
输出包含一个正整数,表示最多可能组成完整书册的数目。
输入输出样例
输入 #15 3 4 5 4 3 2 2 5 2 5 1 5 3 5 1 3 3 1 2 2 3 3 4 3输出 #1
2
说明/提示
样例说明:
如题,N1=5,N2=3,N3=4,表示书有5本、练习册有3本、答案有4本。
M1=5,表示书和练习册共有5个可能的对应关系,分别为:书4和练习册3、书2和练习册2、书5和练习册2、书5和练习册1以及书5和练习册3。
M2=5,表示数和答案共有5个可能的对应关系,分别为:书1和答案3、书3和答案1、书2和答案2、书3和答案3以及书4和答案3。
所以,以上情况的话最多可以同时配成两个书册,分别为:书2+练习册2+答案2、书4+练习册3+答案3。
数据规模:
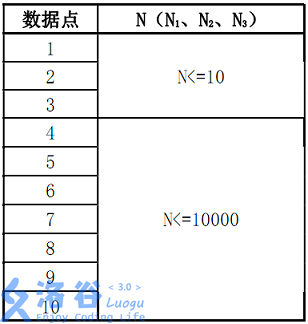
对于数据点1, 2, 3,M1,M2<= 20
对于数据点4~10,M1,M2 <= 20000
思路
紫题?就这?
一读题就是老拆点最大流了。
但还是有几个要注意的地方。
一开始没拆点,直接wa7个点,仔细看了题,每本书只能用一次。
如果每本书能用无数次求有几种组合方式当然是不用拆的,直接跑ISAP求最大流就可以了。
其次,这道题卡了优化,一开始懒得上ISAP交了一个没优化的 Dinic T了7个点,炸点+当前弧优化的dinic肯定也是能过的,但肯定没ISAP快。
CODE
#include<cstdio> #include<iostream> #include<cstring> #include<queue> #include<vector> #include<algorithm>
using namespace std;
const int maxn = 1e6 + 7; const int inf = 0x3f3f3f3f;
template<class T>inline void read(T &res) { char c;T flag=1; while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0'; while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag; }
struct edge{int from,to,cap,flow;};
struct isap { int n,s,t,p[maxn],d[maxn],cur[maxn],num[maxn]; bool vis[maxn]; vector<int>g[maxn]; vector<edge>edges; void init(int n,int s,int t) { this->n = n; this->s = s; this->t = t; for(int i = 1;i <= n;i++) g[i].clear(); edges.clear(); } void addegde(int from,int to,int cap) { edges.push_back((edge){from, to, cap, 0}); edges.push_back((edge){to, from, 0, 0}); int m = edges.size(); g[from].push_back(m-2); g[to].push_back(m-1); }
int augment() {///找增广路 int x = t,a = inf; while(x!=s) { a = min(a, edges[p[x]].cap - edges[p[x]].flow); x = edges[p[x]].from; } x=t; while(x != s) { edges[p[x]].flow += a; edges[p[x]^1].flow = -a; x = edges[p[x]].from; } return a; } int maxflow() {///更新最大流 int flow = 0; memset(num, 0, sizeof(num)); memset(cur, 0, sizeof(cur)); for(int i = 1; i <= n; i++) num[d[i]]++; int x = s; while(d[s] < n) {///最长的一条链上,最大的下标是nv-1,如果大于等于nv说明已断层 if(x == t) { flow += augment(); x = s;//回退 } bool ok = 0; for(int i = cur[x]; i < g[x].size(); i++) { edge &e = edges[g[x][i]]; if(d[x] == d[e.to] + 1 && e.cap > e.flow) { p[e.to] = g[x][i]; cur[x] = i;x = e.to; ok = 1; break; } } if(!ok) { int m = n-1; for(int i = 0; i < g[x].size();i++) { edge &e=edges[g[x][i]]; if(e.cap>e.flow) m=min(m,d[e.to]); } num[d[x]]--; if(!num[d[x]]) break; d[x] = m+1; num[d[x]]++; cur[x] = 0; if(x != s) x = edges[p[x]].from; } } return flow; } }ISAP;
int n, p, q; int s, t;
int main() { read(n), read(p), read(q); s = 2*n+q+p+1; t = s+1; ISAP.init(2 * n + p + q + 7, s, t); int m2; read(m2); for ( int i = 1; i <= m2; ++i ) { int u, v; read(u); read(v); ISAP.addegde(v, u + p, 1); } read(m2); for ( int i = 1; i <= m2; ++i ) { int u, v; read(u);read(v); ISAP.addegde(n + p + u, v + p + 2 * n, 1); } for ( int i = 1; i <= n; ++i ) { ISAP.addegde(p + i, n + p + i, 1); } for ( int i = 1; i <= q; ++i ) { ISAP.addegde(s, i, 1); } for ( int i = 1; i <= p; ++i ) { ISAP.addegde(n * 2 + p + i, t, 1); } // while(bfs()) { // Dinic(); // } printf("%d\n",ISAP.maxflow()); return 0; }
标签:int,flow,教辅,网络,read,P1231,答案,练习册,ISAP 来源: https://www.cnblogs.com/orangeko/p/12562890.html