最大堆的简单实现

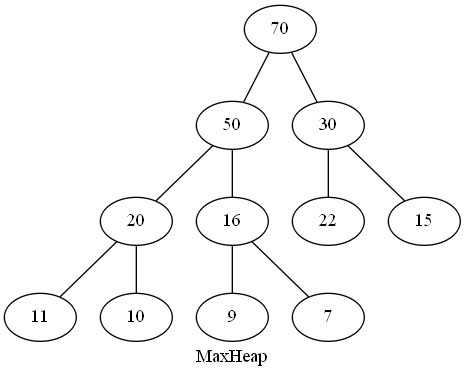
二叉堆是一棵完全二叉树，完全二叉树：对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

可以理解为将数据按照“层序遍历”的方式排列到二叉树的每一个节点，完全二叉树不一定是满二叉树，完全二叉树缺少的部分在树的右下方。

如果堆中某个节点的值总是不大于其父节点的值，那么这种堆就是最大堆。

由于最大堆的元素是按照一层一层的顺序排列的，所以我们可以使用数组来作为底层数据结构来实现最大堆，当然也可以使用树结构实现。

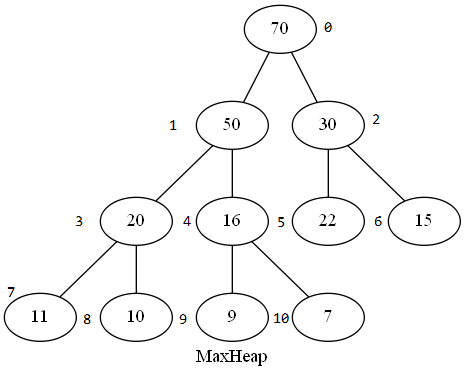
以数组的形式表现的最大堆差不多是这样的：

那么要怎样区分哪些节点是父节点，哪些节点是孩子节点？
我们可以发现左孩子节点的偏移是父节点的2倍然后+1，右孩子节点是父节点的2倍+2。

parent(i) = (i - 1) / 2

leftChild(i) = 2 * i + 1

rightChild(i) = 2 * i +2

用我之前的动态数组来实现最大堆：

public class MaxHeap<E extends Comparable<E>> {

    //使用动态数组作为基础数据结构实现最大堆
    private Array<E> data;

    //构造函数---指定容量
    public MaxHeap(int capacity) {
        data = new Array(capacity);
    }

    public MaxHeap() {
        data = new Array();
    }
}

接下来是获取各个节点索引的方法的实现：

//返回完全二叉树的数组表示中，index索引所表示的元素的父亲节点的索引
private int parent(int index) {
    if (index == 0)
        throw new IllegalArgumentException("index-0 doesn't have parent.");
    return (index - 1) / 2;
}

//返回index索引所表示的元素的左孩子节点的索引
private int leftChild(int index) {
    return index * 2 + 1;
}

//返回index索引所表示的元素的右孩子节点的索引
private int rightChild(int index) {
    return index * 2 + 2;
}

两个简单的方法：

//返回堆中的元素个数
public int size() {
    return data.getSize();
}

//判断堆中是否为空
public boolean isEmpty() {
    return data.isEmpty();
}

向最大堆中添加元素：

如果添加的元素比父节点还大，那么就破坏了最大堆的定义，因此我们需要调整，把添加的元素和父节点对比，然后判断是否更换位置，如果更换位置了，那么就要再对比新的父节点，然后判断是否更换位置，以此类推。

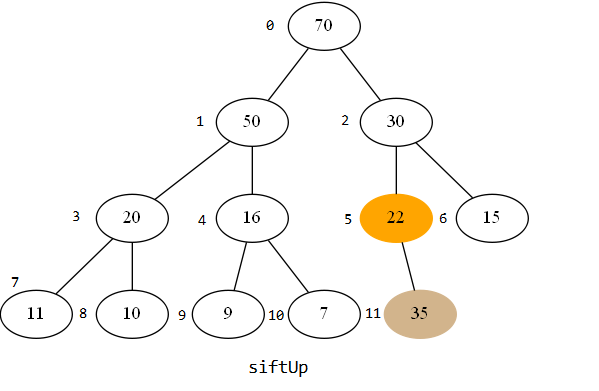
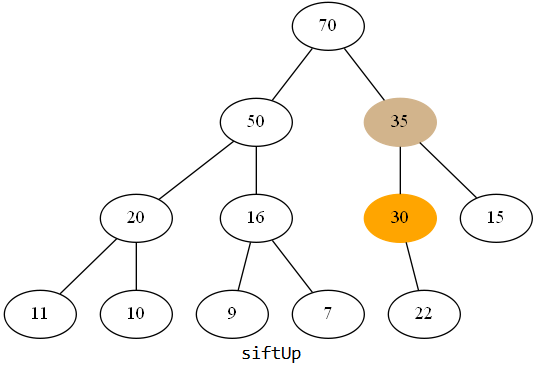
比如我添加了一个元素35：

可以看到35比父节点还大，所以要更换位置("上浮")，效果差不多是这样的：

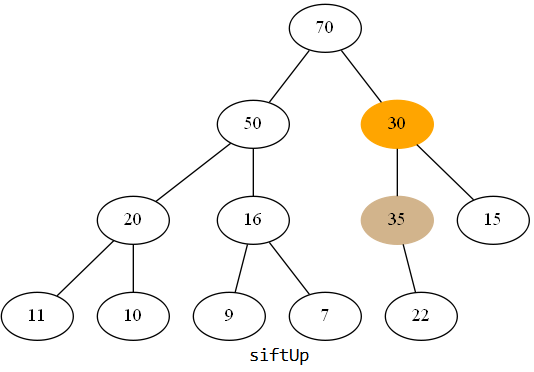
但是我们更换位置后，却发现比新的父节点还大，因此还要更换位置：

元素这样排列才是符合最大堆定义的。

具体的"上浮"方法和添加元素方法：

//上浮方法
private void siftUp(int i) {
    //i不能到达根节点，因为根节点没有父节点
    while (i > 0 && data.get(parent(i)).compareTo(data.get(i)) < 0) {
        data.swap(i, parent(i));
    //重新赋值i
        i = parent(i);
    }
}

//向堆中添加元素
public void add(E e) {
    data.addLast(e);
    //上浮,传入将可能要上浮的元素所在的索引
    siftUp(data.getSize() - 1);
}

查看堆中最大元素的方法

//查看堆中的最大元素
public E findMax() {
    if (data.getSize() == 0)
        throw new IllegalArgumentException("Heap is Empty");
    return data.get(0);
}

从堆中取出最大元素：

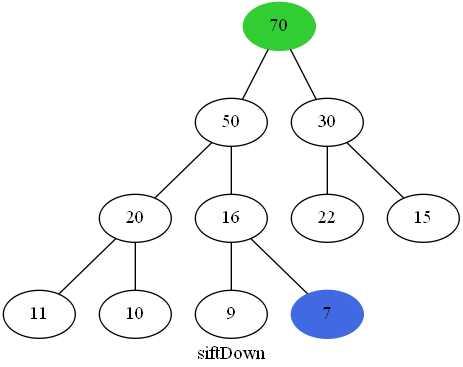
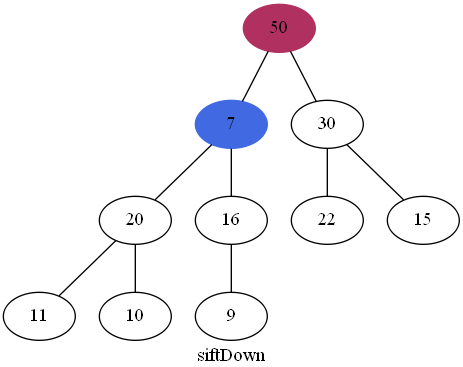
在最大堆中只能取出堆中最大的元素，我们把根节点取出删除后，堆就变成两棵树，把两棵树合成一棵比较麻烦，我们可以先将最后一个节点换到根节点，然后把最后一个节点删除，但是此时的堆是不满足最大堆的定义的，因此需要对根节点进行"下沉"操作。

交换元素

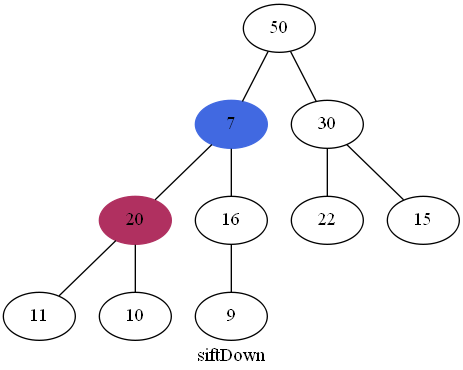
在删除最后一个节点后，就需要对根节点进行"下沉"操作了，首先找出根节点的左右两个孩子节点中最大的一个，将其与根节点进行比较，如果大于根节点，就需要进行交换节点操作，以此循环。

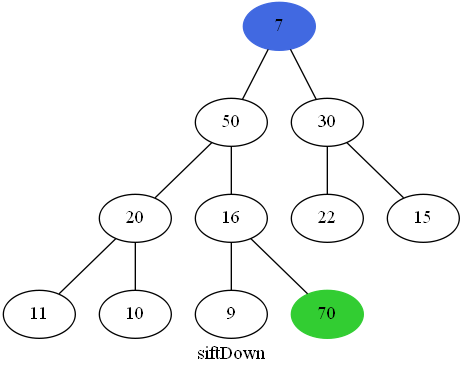
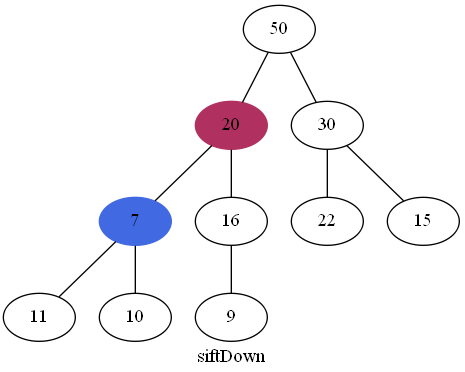
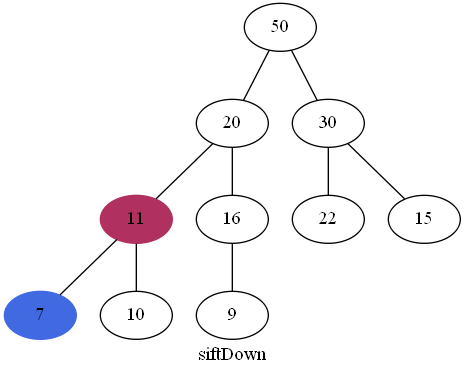
继续"下沉"：

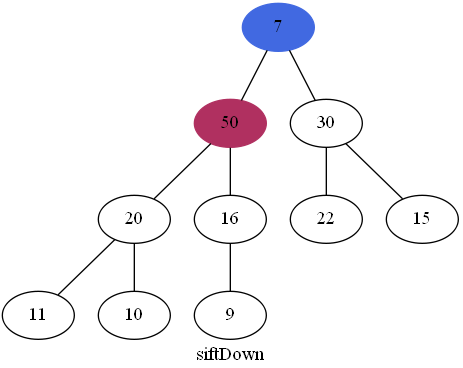
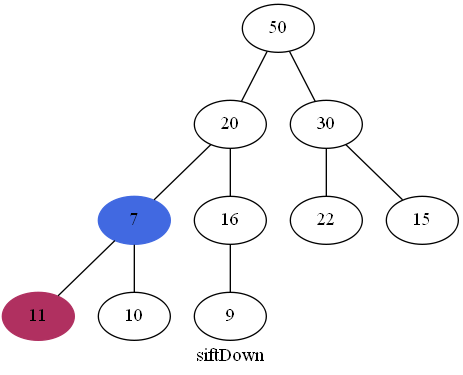
可以看到7比11还小，还需要下沉：

这样才符合最大堆的定义。

下沉方法和取出最大元素的方法：

//下沉方法
private void siftDown(int i) {

    //i的左孩子节点都已经越界了，就说明i已经没有孩子了
    while (leftChild(i) < data.getSize()) {

        //用变量j存储左孩子的索引
        int j = leftChild(i);
        //如果j+1 < getSize，就说明有右孩子节点，并且右孩子节点大于左孩子节点
        if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0)
            //将j赋值为右孩子节点的索引
            j = rightChild(i);
        //如果i索引节点大于或等于j索引的节点，那么不会破坏最大堆的定义，break
        if (data.get(i).compareTo(data.get(j)) >= 0)
            break;
        //否则交换i和j
        data.swap(i, j);
        //重新赋值i
        i = j;
    }
}

//取出堆中的最大元素
public E extractMax() {
    E ret = findMax();
    data.swap(0, data.getSize() - 1);
    data.removeLast();
    siftDown(0);
    return ret;
}

替换堆中最大的元素方法：

//取出堆中的最大元素，并且替换成元素e
public E replace(E e){
    E ret = findMax();
    data.set(0,e);
    siftDown(0);
    return ret;
}

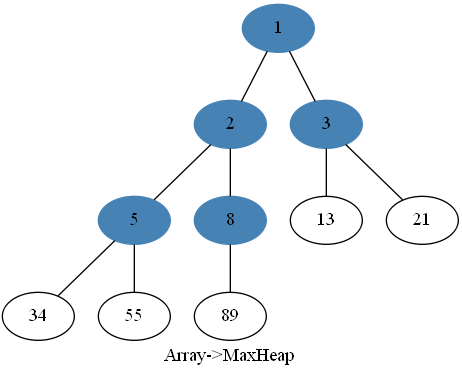
最后可以写个构造函数用于传入一个数组然后构造出最大堆：

//构造函数---传入arr数组并且构造最大堆
public MaxHeap(E[] arr) {
    data = new Array<>(arr);
    for (int i = parent(arr.length - 1); i >= 0; i--) {
        siftDown(i);
    }
}

这里for循环的变量i控制的是每个非叶子节点的顺序，从最后一个非叶子节点到根节点的顺序。 siftDown保证了每个非叶子节点的"下沉"。

标签：index,最大,实现,元素,堆中,int,简单,data,节点
来源： https://www.cnblogs.com/AACFHFZFZE/p/12536487.html