10.17 模拟赛
作者:互联网
10.17 模拟赛
T1
直接看题解吧,懒得写了,和前天T2的思路差不多
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<bitset>
#include<set>
using namespace std;
//#define int long long
typedef long long ll;
#define MAXN 200006
#define MAXM 450
#define pb push_back
#define pii pair<int,int>
#define fi first
#define se second
#define mp make_pair
#define inf 0x3f3f3f3f
#define cmx( a , b ) a = max( a , b )
#define cmn( a , b ) a = min( a , b )
#define upd( a , b ) ( a = ( a + b ) % P )
#define P 998244353
void read( signed& x ) {
scanf("%d",&x);
}
void read( ll& x ) {
scanf("%lld",&x);
}
int n , m , x0;
int rd( ) {
return ( x0 = ( ( 1ll * 100000005 * x0 + 20150609 ) % P ) )/ 100;
}
int mx[MAXN << 2] , mn[MAXN << 2] , rev[MAXN << 2];
inline void poi( int rt ) {
mx[rt] = max( mx[rt << 1] , mx[rt << 1 | 1] ) , mn[rt] = min( mn[rt << 1] , mn[rt << 1 | 1] );
}
#define swap( a , b ) a=a^b,b=a^b,a=a^b
#define di( a ) ( a = ( 100000 - a ) )
inline void rever( int rt ) {
swap( mx[rt] , mn[rt] ) , di( mx[rt] ) , di( mn[rt] ) , rev[rt] ^= 1;
}
inline void pd( int rt ) {
if( rev[rt] )
rever( rt << 1 ) , rever( rt << 1 | 1 ) , rev[rt] = 0;
}
void build( int rt , int l , int r ) {
if( l == r ) { mx[rt] = mn[rt] = rd() % 100001; return; }
int m = l + r >> 1;
build( rt << 1 , l , m ) , build( rt << 1 | 1 , m + 1 , r );
poi( rt );
}
void mdfy( int rt , int l , int r , int L , int R ) {
if( L <= l && R >= r ) { rever( rt ); return; }
pd( rt );
int m = l + r >> 1;
if( L <= m ) mdfy( rt << 1 , l , m , L , R );
if( R > m ) mdfy( rt << 1 | 1 , m + 1 , r , L , R );
poi( rt );
}
void mdf( int rt , int l , int r , int p , int c ) {
if( l == r ) { mx[rt] = mn[rt] = c; return; }
pd( rt );
int m = l + r >> 1;
if( p <= m ) mdf( rt << 1 , l , m , p , c );
else mdf( rt << 1 | 1 , m + 1 , r , p , c );
poi( rt );
}
int a , b , c;
inline ll calc( int x , int y ) {
return 1ll * a * x + 1ll * b * y + 1ll * c * x * y;
}
ll curans = 0;
void query( int rt , int l , int r , int L , int R ) {
if( l == r ) { curans = calc( l , mx[rt] ); return; }
pd( rt );
int m = l + r >> 1;
if( R > m && calc( r , mx[rt << 1 | 1] ) > curans ) query( rt << 1 | 1 , m + 1 , r , L , R );
if( L <= m && calc( m , mx[rt << 1] ) > curans ) query( rt << 1 , l , m , L , R );
}
int main() {
// freopen("conic.in","r",stdin);
// freopen("conic.out","w",stdout);
read( n ) , read( m ) , read( x0 );
char opt[10];
build( 1 , 1 , n );
int p , q , y;
while( m --> 0 ) {
scanf("%s",opt);
if( opt[0] == 'C' ) { p = rd() % n + 1 , q = rd() % 100001 , mdf( 1 , 1 , n , p , q ); }
else if( opt[0] == 'R' ) { p = rd() % n + 1 , q = rd() % n + 1; if( p > q ) swap( p , q ); mdfy( 1 , 1 , n , p , q ); }
else if( opt[0] == 'Q' ) { read(a),read(b),read(c); p = rd() % n + 1 , q = rd() % n + 1; if( p > q ) swap( p , q ); curans = 0; query( 1 , 1 , n , p , q ); printf("%lld\n",curans); }
}
}T2
看数据范围会考虑网络流。
考虑对于两个 B 原子,如果满足条件一定一个在奇数行一个在偶数行。于是我们把奇数行的 B 放左边,偶数行放右边,然后对于所有 A 拆点连边跑最大流即可。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<bitset>
#include<set>
using namespace std;
//#define int long long
typedef long long ll;
#define MAXN 1006
#define MAXM 450
#define pb push_back
#define pii pair<int,int>
#define fi first
#define se second
#define mp make_pair
#define inf 0x3f3f3f3f
#define cmx( a , b ) a = max( a , b )
#define cmn( a , b ) a = min( a , b )
#define upd( a , b ) ( a = ( a + b ) % P )
#define P 998244353
void read( signed& x ) {
scanf("%d",&x);
}
void read( ll& x ) {
scanf("%lld",&x);
}
int n , m , s , t;
#define maxm 5000006
#define maxn 500000
#define rep(ii, a, b) for (int ii = a; ii <= b; ++ii)
#define per(ii, a, b) for (int ii = b; ii >= a; --ii)
#define IO \
ios::sync_with_stdio(false); \
cin.tie(0); \
cout.tie(0)
#define show(x) cout << #x << "=" << x << endl
#define show2(x, y) cout << #x << "=" << x << " " << #y << "=" << y << endl
#define show3(x, y, z) cout << #x << "=" << x << " " << #y << "=" << y << " " << #z << "=" << z << endl
#define show4(w, x, y, z) \
cout << #w << "=" << w << " " << #x << "=" << x << " " << #y << "=" << y << " " << #z << "=" << z << endl
#define show5(v, w, x, y, z) \
cout << #v << "=" << v << " " << #w << "=" << w << " " << #x << "=" << x << " " << #y << "=" << y << " " \
<< #z << "=" << z << endl
#define showa(x, a, b) \
cout << #x << ": "; \
rep(i, a, b) cout << x[i] << ' '; \
cout << endl
template <typename T>
class mxf {
public:
struct node {
int to, next;
T cap;
} e[maxm];
int cur[maxn], head[maxn], dis[maxn], gap[maxn];
int nume = 1, s, t, tot;
void init(int n) {
rep(i, 0, n) head[i] = gap[i] = dis[i] = 0;
nume = 1;
}
void add(int a, int b, T c) {
e[++nume] = { b, head[a], c };
head[a] = nume;
e[++nume] = { a, head[b], 0 };
head[b] = nume;
}
T dfs(int now, T flow) {
if (now == t || flow <= 0)
return flow;
T use = 0, tmp;
int d = dis[now] - 1, to;
for (int &i = cur[now]; i; i = e[i].next) {
if (dis[to = e[i].to] == d && (tmp = e[i].cap)) {
e[i].cap -= (tmp = dfs(to, min(flow - use, tmp)));
e[i ^ 1].cap += tmp;
if ((use += tmp) == flow)
return use;
}
}
if (!--gap[dis[now]])
dis[s] = tot + 1;
++gap[++dis[now]];
cur[now] = head[now];
return use;
}
ll getflow(int ss, int tt, int n) {
tot = n;
s = ss;
t = tt;
gap[0] = tot;
ll ans = 0;
memcpy(cur, head, (tot + 1) << 2);
while (dis[s] <= tot) ans += dfs(s, 0x7fffffff);
return ans;
}
};
mxf<int> net;
int G[MAXN][MAXN] , id[MAXN][MAXN] , cn;
int main() {
// freopen("molecule.in","r",stdin) , freopen("molecule.out","w",stdout);
read( n ) , read( m );
for( int i = 1 , s ; i <= n ; ++ i )
for( int j = 1 ; j <= m ; ++ j ) {
scanf("%d",&s);
if( s == 2 ) id[i][j] = ++ cn;
else if( s == 1 ) G[i][j] = 1;
}
for( int i = 1 ; i <= n ; ++ i )
for( int j = 1 ; j <= m ; ++ j ) if( G[i][j] ) {
++ cn; net.add( cn , cn + 1 , 1 );
if( i & 1 ) {
if( id[i - 1][j] ) {
if( id[i][j - 1] ) net.add( id[i - 1][j] , cn , 1 ) , net.add( cn + 1 , id[i][j - 1] , 1 );
if( id[i][j + 1] ) net.add( id[i - 1][j] , cn , 1 ) , net.add( cn + 1 , id[i][j + 1] , 1 );
}
if( id[i + 1][j] ) {
if( id[i][j - 1] ) net.add( id[i + 1][j] , cn , 1 ) , net.add( cn + 1 , id[i][j - 1] , 1 );
if( id[i][j + 1] ) net.add( id[i + 1][j] , cn , 1 ) , net.add( cn + 1 , id[i][j + 1] , 1 );
}
} else {
if( id[i][j - 1] ) {
if( id[i - 1][j] ) net.add( id[i][j - 1] , cn , 1 ) , net.add( cn + 1 , id[i - 1][j] , 1 );
if( id[i + 1][j] ) net.add( id[i][j - 1] , cn , 1 ) , net.add( cn + 1 , id[i + 1][j] , 1 );
}
if( id[i][j + 1] ) {
if( id[i - 1][j] ) net.add( id[i][j + 1] , cn , 1 ) , net.add( cn + 1 , id[i - 1][j] , 1 );
if( id[i + 1][j] ) net.add( id[i][j + 1] , cn , 1 ) , net.add( cn + 1 , id[i + 1][j] , 1 );
}
}
++ cn;
}
s = ++ cn , t = ++ cn;
for( int i = 1 ; i <= n ; ++ i )
for( int j = 1 ; j <= m ; ++ j ) if( id[i][j] )
if( ( ~i ) & 1 )
net.add( s , id[i][j] , 1 );
else net.add( id[i][j] , t , 1 );
cout << net.getflow( s , t , t ) << endl;
}
T3
这题的毒瘤就在于精度。。
首先将范围离散化,然后对于一个数考虑它的所有小区间来计算答案。
因为如果考虑小区间就不会有区间相交的情况了,对于每个小区间再枚举所有数,然后就有几种概率,
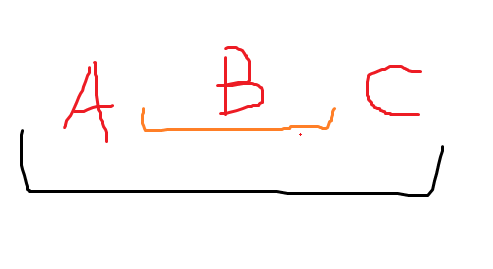
其中橙色的是小区间,黑色是大区间。
用 $ f[i][j][k] $ 表示当前在处理 $ i $ 区间,一共有 $ j $ 个位置一定在这个区间前面,有 $ k $ 个位置是在这个区间内随机的概率。
那么$ f[i][j][k] = f[i - 1][j - 1][k] \times A + f[i - 1][j][k - 1] \times B + f[i - 1][j][k] \times C $
如何统计答案呢?如果用 ans 来记录枚举的这个数是 rank i 的概率,可以枚举在这个数字之前的个数 p 以及在这个数字之中的个数。由于在这个数字中出现是随机的,所以 rank p ~ p + k 的概率其实是一样的,就是 $ dp $ 值除以 $ k + 1 $。这里的加可以用差分最后在输出前缀和,其实没有也可以,复杂度不变。
总复杂度大概是$ O(n^5) $
据说不考虑精度可以有 $ O(n^4) $ 做法。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<bitset>
#include<set>
using namespace std;
//#define int long long
//#define double long double
typedef long long ll;
#define MAXN 86
#define MAXM 450
#define pb push_back
#define pii pair<int,int>
#define fi first
#define se second
#define mp make_pair
#define inf 0x3f3f3f3f
#define cmx( a , b ) a = max( a , b )
#define cmn( a , b ) a = min( a , b )
#define upd( a , b ) ( a = ( a + b ) % P )
#define P 998244353
void read( signed& x ) {
scanf("%d",&x);
}
void read( ll& x ) {
scanf("%lld",&x);
}
int n;
double dp[2][MAXN][MAXN];
int L[MAXN] , R[MAXN];
double ans[MAXN * 2]; int pos[MAXN << 1] , en;
int main() {
read( n );
for( int i = 1 ; i <= n ; ++ i )
read( L[i] ) , read( R[i] ) , pos[++ en] = L[i] , pos[++ en] = R[i];
sort( pos + 1 , pos + 1 + en );
int sz = unique( pos + 1 , pos + 1 + en ) - pos - 1;
for( int i = 1 ; i <= n ; ++ i ) {
int l = L[i] , r = R[i] , ct = 0;
memset( ans , 0 , sizeof ans );
for( int j = 1 ; j < sz ; ++ j ) {
ct = 0;
int ll = pos[j] , rr = pos[j + 1];
if( l > ll || r < rr ) continue;
int cur = 0; memset( dp , 0 , sizeof dp ) , dp[0][0][0] = (double)( rr - ll ) / ( r - l );
for( int k = 1 ; k <= n ; ++ k ) if (k != i) {
if( R[k] <= ll ) { ++ ct; continue; }
if( L[k] >= rr ) continue;
double A = (double)( ll - L[k] ) / ( R[k] - L[k] );
double B = (double)( rr - ll ) / ( R[k] - L[k] );
double C = (double)( R[k] - rr ) / ( R[k] - L[k] );
cur ^= 1; memset( dp[cur] , 0 , sizeof dp[cur] );
for( int ls = 0 ; ls <= k ; ++ ls )
for( int kel = 0 ; kel <= k - ls ; ++ kel )
dp[cur][ls + 1][kel] += dp[cur ^ 1][ls][kel] * A,
dp[cur][ls][kel + 1] += dp[cur ^ 1][ls][kel] * B,
dp[cur][ls][kel] += dp[cur ^ 1][ls][kel] * C;
}
for( int ls = 0 ; ls <= n ; ++ ls )
for( int k = 0 ; k <= n - ls ; ++ k ) {
double v = dp[cur][ls][k] / ( k + 1 );
for( int aa = ct + ls ; aa <= ct + ls + k ; ++ aa ) ans[aa] += v;
}
}
for( int j = 1 ; j <= n ; ++ j )
printf("%.8lf " , ans[n - j]);
puts("");
}
}标签:int,long,read,MAXN,10.17,include,模拟,define 来源: https://www.cnblogs.com/yijan/p/1017comp.html