时间、空间复杂度推导

时间复杂度公式推导

首先假设每一行的代码执行时间是相同的

推导过程

案例

def zx(n):
    sum = 0
    for i in range(n):
        sum += 1
    print(sum)

那么这个函数执行花费的时间为2n+1*time

def zx(n):
    sum = 0
    for i in range(n):
        for i in range(n):
            sum +=1
    print(sum)

这个函数的执行花费时间为$2n^2$+n+1*time

总结

$T_(n)$表示代码执行的时间，n表示数据的规模，$f_(n)$表示每行代码执行次数的总和，O表示执行花费总时间和执行代码总次数成正比

$T_(n)$=O($f_(n)$)

当n的数据规模很大的时候，案例中的个位数的代码执行次数可以忽略不计，同时低阶和系数的影响也是可以忽略的，最后得出两段代码的时间复杂度为

$T_(n)$=O(2n+1)=O(n)

$T_(n)$=O(2$n^2$+n+1)=O($n^2$）

时间复杂度排序

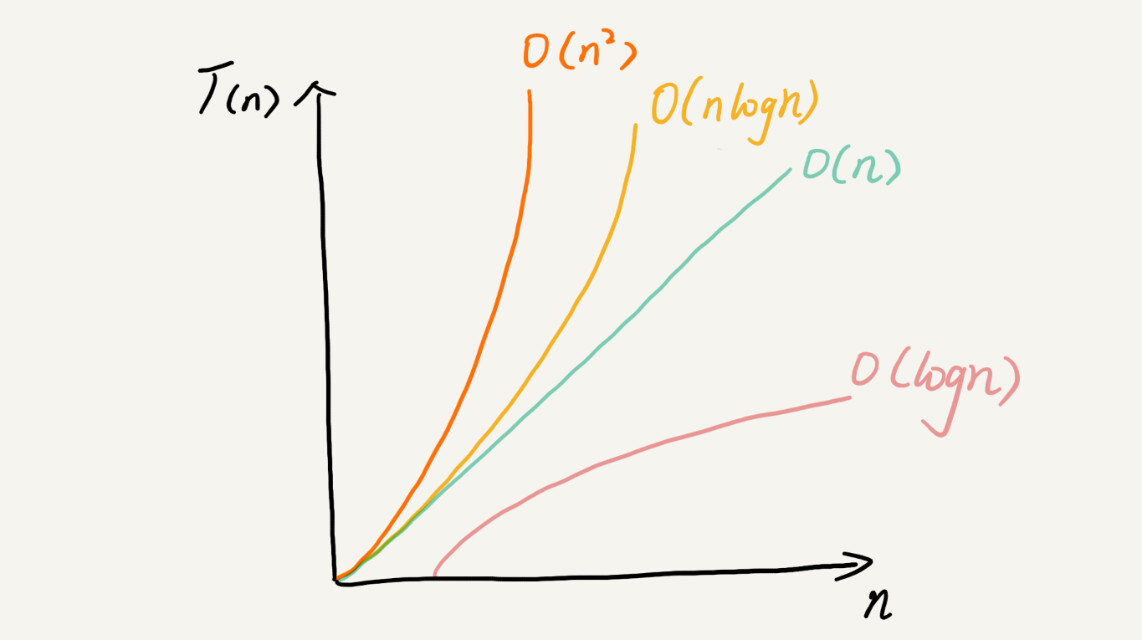
常数阶O(1)

a = 1
b = 2
c = a+b

一般情况下，只要代码的执行时间不随n的增大而增大，这样代码的时间复杂度我们就记作O(1)

对数阶O($log$n)和O（n$log$n）

def zx(n):
    i = 1
    while i <= n:
        i = i * 2
    print(i)

T(n)=O($log_2$n)=$logn$

def zx(n):
    i = 1
    while i <= n:
        i = i * 3
    print(i)

T(n)=O($log_3$n)=$logn$

def zx(n):
    for i in range(n):
        i = 1
        while i <= n:
            i = i * 2

T(n)=O(n$log_3$n)=n$logn$

多参数时间复杂度分析O(m+n),O(m*n)

与单参数时间复杂度的区别

多参数

def zx(m,n):
    sum = 0
    for i in range(m):
        sum += 1
    for i in range(n):
        sum += 1
    print(sum)

时间复杂度为T(m+n)=O(m)+O(n)=O(m+n)
单参数

def zx(n):
    sum = 0
    for i in range(n):
        sum += 1
    for i in range(n):
        sum += 1
    print(sum)

时间复杂度为T(m+n)=O(n)

O(m*n)和O(n*n)是一样的规律

空间复杂度

空间复杂度O(1)

int i = 1
int j = 2

此算法的空间复杂度为一个常量，表示为O(1)

空间复杂度O(n)

void zx(int n){
    int [] a = new int[n];
}

我们申请了一个空间为n的int数组，而且它和参数有关，所以此段的空间复杂度为O(n)

标签：推导,int,复杂度,range,zx,空间,sum,def
来源： https://www.cnblogs.com/zx125/p/11668908.html